AP Syllabus focus:
‘Given a slope field, students sketch approximate solution curves by following the pattern of the line segments, visualizing how solutions to the differential equation behave.’
Interpreting solution curves from a slope field involves visualizing how a function behaves based on local slope information, allowing students to understand differential equation solutions without solving analytically.
Understanding Solution Curves in a Slope Field
A slope field is a graphical representation of a first-order differential equation using a grid of short line segments. Each segment’s tilt shows how a solution curve would locally rise or fall if it passed through that point. Because slope fields summarize directional behavior without requiring explicit formulas, they provide a powerful qualitative tool for understanding how differential equations predict change.
When a student traces a path that follows the displayed slopes, the result is an approximate solution curve, which represents a possible function whose derivative at each point matches the differential equation.
Slope Field: A diagram of short line segments showing the slope at many points for a first-order differential equation.
A solution curve must always be tangent to the slope segments it passes through.
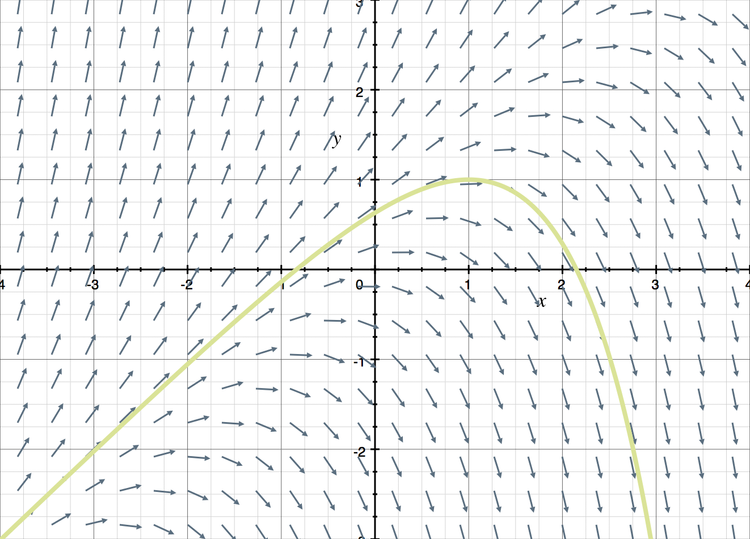
A direction field for a first-order differential equation with one highlighted solution curve passing through a chosen initial point. The curve remains tangent to the line segments, demonstrating how a particular solution is determined. Extra surrounding algebra on the page is not required by the AP syllabus, but the visual relationship between field and curve directly supports it. Source.
This idea ensures consistency with the underlying differential equation and helps students predict behavior even in unfamiliar contexts.
The Relationship Between a Differential Equation and Its Solution Curves
A slope field is constructed from a given first-order differential equation, which expresses the derivative of a function in terms of the variables.
= instantaneous rate of change of with respect to
= rule assigning a slope at each point
The slope field provides an immediate sense of the structure of solution families by showing slope patterns instead of relying on algebraic manipulation.
Visual Cues When Following Slope Segments
Students should attend closely to how slopes vary across the plane, because those variations determine how solution curves bend or change direction. Important visual cues include:
Patterns of increasing or decreasing slopes, indicating accelerating or slowing growth.
Horizontal line segments, which reveal where and suggest possible constant solutions.
Regions with positive slopes, where solution curves rise as increases.
Regions with negative slopes, where solution curves fall as increases.
Changes in slope steepness, which indicate how rapidly the dependent variable responds to changes in the independent variable.
Because the solution curve must remain tangent to each local segment, students build the curve by smoothly connecting these directional hints.
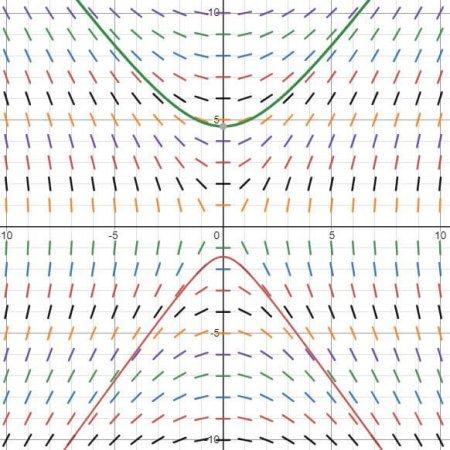
A slope field for with two superimposed solution curves. Each curve closely follows the local slope segments, illustrating how solutions evolve within the field. The inclusion of visible maxima and minima extends slightly beyond the AP requirement but remains helpful in visualizing qualitative behavior. Source.
Families of Solution Curves
Slope fields typically depict many possible solutions rather than one unique function. These curves form a family of solutions, representing the range of possible functions satisfying the differential equation for different initial conditions.
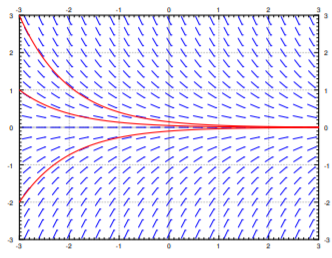
A slope field for with three solution curves corresponding to different initial values. Each curve remains tangent to the local slopes, illustrating the idea of a family of solutions. The figure also shows how small changes in initial conditions yield noticeably different solution paths, which goes slightly beyond but supports AP-level understanding. Source.
Family of Solutions: A set of solution curves corresponding to the same differential equation but different starting values or initial conditions.
Recognizing these families helps students understand that differential equations often predict multiple behaviors depending on initial values.
How to Trace a Solution Curve on a Slope Field
When interpreting a slope field, students mentally or physically sketch a curve that aligns with the direction of the slope segments. A systematic approach includes:
Identify a point of interest, often given in a context or as an initial condition.
Observe the local slope at that point to determine the initial direction of the solution curve.
Move slightly in the -direction, adjusting the curve so that it stays tangent to the displayed segments.
Continue tracing, following changes in segment orientation as the curve progresses.
Maintain smoothness, ensuring that the curve does not kink or abruptly change direction.
Avoid crossing other solution curves, since uniqueness guarantees that solutions do not intersect.
This process trains students to visualize solution behavior even without explicit formulas.
Understanding Qualitative Behavior from Solution Curves
Interpreting solution curves extends beyond tracing them. Students analyze the qualitative behavior suggested by the slope field, such as:
Long-term tendencies, including growth, decay, or leveling off
Sensitivity to initial conditions and how curves diverge or converge
Stability of horizontal trajectories when
Regions where solutions change rapidly due to steep slopes
Overall shape characteristics, such as concavity or asymmetry
These insights help students connect graphical information with the ideas of change, rate, and functional behavior central to differential equations.
Connecting Interpretation to the AP Syllabus
The AP focus emphasizes that students must be able to sketch approximate solution curves by following the pattern of the line segments. This includes recognizing how slope information guides the path of a function and visualizing the behavior of solutions arising from a differential equation. Interpreting solution curves is a foundational skill for reasoning about differential equations in both graphical and contextual settings.
FAQ
Solution curves drawn by hand from a slope field are qualitative approximations rather than precise representations.
They capture overall behaviour, such as increasing or decreasing trends, points of flattening, and general curvature.
Accuracy depends on:
• The density of the slope segments
• How carefully the curve follows the indicated directions
• Whether the slope field itself was generated correctly
More densely drawn fields usually give better approximations, but exact accuracy still requires analytical or numerical methods.
If two curves intersected, they would share the same point with different slopes, which would contradict the idea that a differential equation assigns a single slope to each point in the plane.
This uniqueness arises from the differential equation defining one rate of change at every location.
As a result, each curve must remain distinct unless a region of non-uniqueness exists, which is beyond the scope of this subsubtopic.
Even though equilibrium solutions are formally introduced elsewhere, slope fields provide hints through visual cues.
Look for:
• Horizontal line segments over a region
• Slopes that approach zero as curves move towards a line
• Regions where solution curves appear to flatten
These features suggest where solutions may stabilise or level off, even without solving the differential equation.
Slope fields provide a way to reason about behaviour without needing an explicit solution.
They allow you to:
• Judge whether solutions increase or decrease
• Predict long-term tendencies such as levelling off or rapid growth
• Compare how different initial conditions affect the trajectory
This makes slope fields especially valuable for complex equations where traditional algebraic methods fail.
Frequent errors include drawing curves that ignore the slope direction or that intersect other curves.
To avoid this:
• Check the slope orientation at each point the curve passes through
• Keep the curve smooth and continuously aligned with the local slope
• Avoid crossing existing solution paths, which would violate uniqueness
• Resist adding sudden bends or corners that do not match the slope pattern
Careful attention to these details greatly improves the accuracy of sketches.
Practice Questions
Question 1 (1–3 marks)
The slope field for a differential equation dy/dx = f(x, y) is shown. A curve passes through the point (0, 1).
(a) Sketch the solution curve passing through (0, 1) by following the slope segments.
(b) State one feature of your curve that shows it is a valid solution to the differential equation.
Question 1
(a)
• 1 mark: Curve is drawn smoothly through (0, 1).
• 1 mark: Curve remains tangent to slope segments throughout.
(b)
• 1 mark: States that the curve is always tangent to the small line segments / follows the slope pattern / matches the indicated direction of change.
Total: 2–3 marks depending on detail.
Question 2 (4–6 marks)
The slope field for a differential equation dy/dx = g(x, y) is provided.
(a) Describe how the slope field indicates whether solutions are increasing or decreasing in the region x > 0.
(b) A particular solution passes through the point (2, 1). Sketch the approximate solution curve using the slope field.
(c) Explain how the behaviour of the slope segments near the line y = 0 affects the long-term behaviour of your solution curve as x increases.
Question 2
(a)
• 1 mark: Identifies that positive slopes indicate increasing solutions, negative slopes indicate decreasing solutions.
• 1 mark: Correctly refers to the slope field behaviour specifically in the region x > 0.
(b)
• 1 mark: Curve passes through (2, 1).
• 1 mark: Curve follows the direction of the slope segments.
• 1 mark: Curve is smooth and does not cross other solution curves that would be inconsistent with the slope field.
(c)
• 1 mark: Describes how slope segments near y = 0 might flatten, steepen, or show directional change.
• 1 mark: Correctly connects this behaviour to the long-term trend of the solution (e.g., approaches a line, diverges, increases, or decreases depending on the slope pattern).
Total: 5–6 marks depending on detail.

