Matching differential equations to slope fields requires recognizing how a derivative expression governs local slope behavior, allowing students to identify which graphical field corresponds to a given differential equation.

Understanding the Purpose of Matching Slope Fields and Differential Equations

Slope fields serve as visual summaries of first-order differential equations by showing how the derivative dictates solution behavior at individual points. In this subsubtopic, the central objective is learning to connect an equation of the form $dy/dx = f(x, y)$ with the patterns of short line segments displayed in a corresponding slope field. Since each segment’s slope is determined by the derivative expression, consistent structural clues in the field allow students to determine which equation generated it.

Key Idea: Slope Patterns Reflect the Derivative Expression

A slope field encodes the value of $dy/dx$ at many points. When the differential equation assigns a particular structure—such as constant slope along certain curves or varying slope based on $x$ or $y$ alone—this structure becomes visible as patterns. Matching an equation to a field therefore relies on recognizing these patterns and relating them to characteristics of the derivative.

Identifying Patterns Connected to Specific Derivative Structures

A variety of clues may appear in a slope field, each tied to features of the derivative expression. AP Calculus AB students benefit from recognizing the following commonly tested relationships:

When the derivative depends only on x

If a slope field shows vertical “bands” of equal slope, the derivative has the form $dy/dx = f(x)$, where slopes depend solely on the horizontal position.
Examples of identifiable patterns include:

• Slope segments with the same orientation for all points in a vertical line.

• Gradual left-to-right change in slope direction while remaining constant up and down the line.

When the derivative depends only on y

If equal slope values occur along horizontal lines, the derivative is of the form $dy/dx = g(y)$, with slope determined by vertical position.
This situation shows:

• Slopes identical across horizontal bands.

• Solutions that may appear to rise or fall consistently depending on the band they start in.

When the derivative depends on both variables

Irregular or diagonally patterned slope changes indicate a relationship such as $dy/dx = f(x, y)$ where both variables influence the slope.
Typical characteristics include:

• Slopes varying in both $x$ and $y$.

• Structure that cannot be simplified into purely vertical or horizontal bands.

Important Terminology Used in This Topic

Students must understand several key terms used when interpreting slope fields.

Slope fields help students visualize families of solutions without computing explicit formulas, making them an essential tool for matching equations to visual representations.

Normal sentence to satisfy formatting rules.

A solution curve reveals how a function evolves over the domain, but matching tasks emphasize the slope field rather than tracing individual solution paths. Any solution curve is a graph drawn so that at each point its tangent line matches the oriented segment of the field at that point.

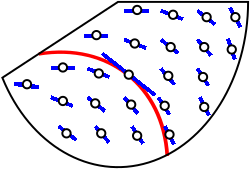
A slope field with a single integral curve. The short line segments show the slope prescribed by $dy/dx = f(x,y)$ at each point, and the smooth curve is a particular solution tangent to the field. Extra detail beyond the syllabus is minimal, keeping the focus on the geometric connection between the field and the differential equation. Source.

Analyzing Structural Features to Choose the Correct Match

When identifying which differential equation corresponds to a specific slope field, consider the following guiding observations:

1. Examine constancy of slope

Look for whether slopes repeat in:

• Vertical lines (implying dependence on $x$)

• Horizontal lines (implying dependence on $y$)

• Neither, suggesting dependence on both $x$ and $y$

This first check eliminates many choices quickly by focusing on broad visual organization.

2. Identify zero-slope lines

A line across which slope segments appear horizontal corresponds to points where $dy/dx = 0$.
These lines provide direct clues about the derivative.
For instance:

• If the slope field shows a horizontal band where slopes appear flat for all $x$, the derivative must equal zero along a constant $y$ value, indicating a factor such as $(y - a)$ appearing in the differential equation.

3. Look for symmetry

Questions often include equations and fields with symmetry in:

• $x$ (even or odd behavior)

• $y$

• origin symmetry

The slope field will mirror this symmetry, allowing quick elimination of asymmetrical options.

4. Observe steepness changes

Some slope fields show rapid shifts from shallow to steep slopes.
This suggests derivative expressions that increase or decrease quickly as a variable changes.
Steepness patterns are especially useful for equations involving multiplicative factors such as $xy$ or $x^2$.

5. Consider direction along diagonals or curves

If the slope field shows uniform slopes along diagonal or curved paths, it indicates the derivative has internal relationships between $x$ and $y$, such as $x + y$, $y - x$, or products of variables.

If a slope field shows vertical “bands” of equal slope, the derivative has the form $dy/dx = f(x)$, where slopes depend solely on the horizontal position.

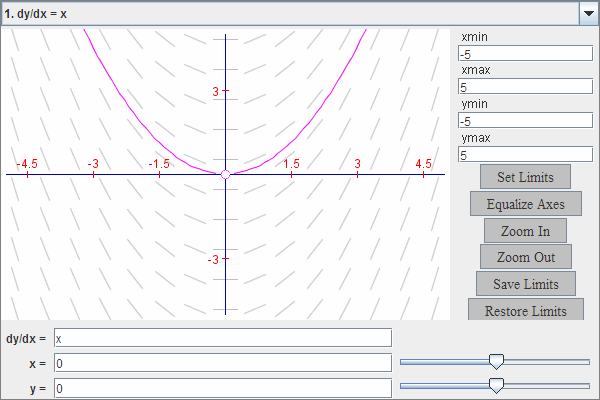
Slope field for the differential equation $dy/dx = x$. Vertical columns of identical slope reflect dependence on $x$ alone. The included solution curve adds minor extra detail but reinforces the required tangent relationship. Source.

If equal slope values occur along horizontal lines, the derivative is of the form $dy/dx = g(y)$, with slope determined by vertical position.

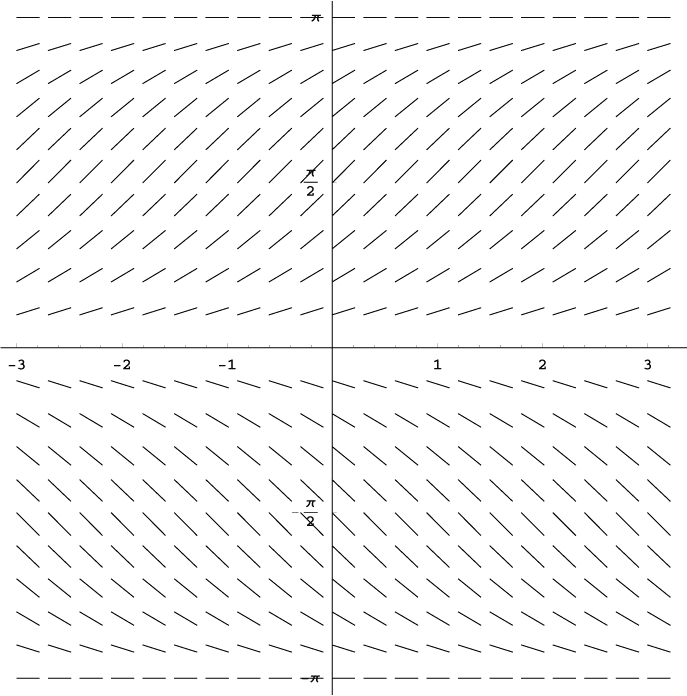
Slope field for an equation of the form $dy/dx = \sin y$. Horizontal bands of identical slope show dependence on the $y$-coordinate only. The dashed lines mark zero-slope rows—additional detail beyond the syllabus but fully consistent with the structure of $g(y)$. Source.

Connecting Visual Evidence to the Given Derivative Expression

When presented with multiple differential equations, students should match them by systematically checking structural clues.
Key strategies include:

• Identifying where slopes are zero and matching those locations to factors of the derivative expression.

• Noting whether slopes increase or decrease with $x$ or with $y$.

• Relating equation components (addition, subtraction, multiplication) to observed patterns, such as diagonal uniformity or region-based slope change.

These processes collectively allow students to determine which equation produced a given slope field or select the correct slope field corresponding to a derivative expression, aligning precisely with the AP syllabus focus for this subsubtopic.