Initial conditions identify a single solution curve within a slope field’s family of possibilities, allowing students to trace a unique path guided by the differential equation’s directional information.

Understanding Particular Solution Curves in Slope Fields

In a slope field, a first-order differential equation provides directional information at each point in the plane. These small line segments illustrate how any solution curve must behave locally, forming a visual summary of all possible solutions. However, without further information, the slope field depicts an infinite family of solutions, each compatible with the differential equation but differing by initial position. To isolate the one solution that applies in a specific situation, an initial condition is required. An initial condition is typically expressed as a point $(x_0, y_0)$ and identifies which member of the family matches the given context.

When learning to interpret slope fields, recognizing how an initial condition selects a unique curve is crucial. A particular solution curve must pass through the given point and follow the slopes at every stage, ensuring consistency with the differential equation’s structure.

The slope field visually communicates this restriction by showing that only one continuous curve can be drawn through the field that both passes through the given point and follows the small segments’ directions.

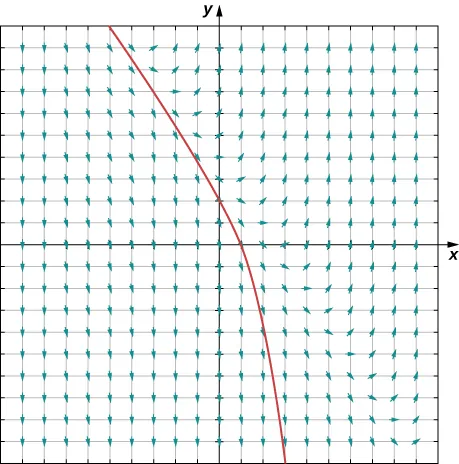
Direction field for the differential equation $y' = 3x + 2y - 4$ with the solution curve passing through the initial condition $(0,1)$. The slope segments illustrate the derivative determined by the differential equation, while the highlighted curve shows the unique particular solution consistent with the initial point. This image includes additional slope field detail but remains fully aligned with the syllabus focus on identifying a particular solution curve. Source.

The Role of Initial Conditions

An initial condition specifies the value of the dependent variable when the independent variable is set to a particular starting value. When first introduced, the term requires clear definition.

A sentence here introduces the next concept before any further structured elements.

The slope field graphically represents this equation by assigning each point a mini-segment with slope $f(x, y)$. Using an initial condition means locating the given point on the coordinate grid, then visually following the local slopes to trace the corresponding particular curve.

Tracing a Particular Solution Curve

To reason effectively about particular solutions using slope fields, students must understand the procedural relationship between directional information and curve construction. The slope field itself shows the structure of the solution family, while the initial condition indicates which piece of that family applies.

Key Process for Tracing a Particular Curve

• Locate the initial condition $(x_0, y_0)$ clearly on the slope field.
• Observe the slope segment at that point, noting its steepness and direction.
• Follow the slope segments forward and backward, sketching a smooth curve that remains tangent to the displayed line segments throughout.
• Avoid crossing or diverging from the local slope patterns, ensuring the curve always aligns with the differential equation’s prescribed direction at each point.
• Maintain continuity, since solution curves to first-order differential equations are continuous and cannot jump between unrelated segments.

This process underscores that the slope field does not merely illustrate rough tendencies; it directly encodes the derivative relationship governing the behavior of the chosen particular solution. Because solutions cannot intersect unless they are identical, the initial condition uniquely identifies the one curve that must be drawn.

Distinguishing Among Members of a Solution Family

A slope field inherently displays many possible solution trajectories, often running parallel or gradually diverging depending on how the differential equation behaves. While the general family of solutions reflects the mathematical freedom introduced by an arbitrary constant in analytic solutions, the slope field displays this concept visually. When no initial condition is provided, any smooth curve that follows the slope pattern may serve as a valid solution. Once the initial condition is imposed, only one of these curves is acceptable.

Once the initial condition is imposed, only one of these curves is acceptable.

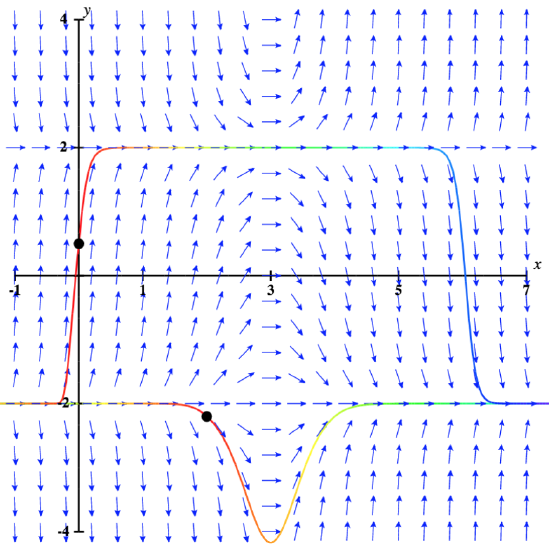
Direction field for the differential equation $y' = (x-3)(y^2-4)$ showing two distinct particular solution curves through different initial conditions. Each curve satisfies the same differential equation but corresponds to its own starting point, visually demonstrating how initial conditions determine unique trajectories. The image also includes horizontal equilibrium lines at $y=-2$ and $y=2$, which extend slightly beyond the exact syllabus requirement but strengthen understanding of solution families. Source.

Visual Clues That Identify the Correct Particular Solution

• The correct curve must pass through the initial point exactly.
• It must align with all slope segments encountered as it evolves, matching the derivative at every stage.
• It must not intersect other solution curves, since first-order differential equations do not permit crossing of distinct solutions.
• It must preserve the qualitative behavior indicated by the slope field, such as whether the function increases, decreases, or levels out.

These aspects highlight how slope fields serve not just as pictures but as reasoning tools. The initial condition allows students to connect mathematical statements with graphical behavior by constraining the solution to a single, meaningful curve.

Importance in Modeling and Interpretation

Using initial conditions to select a particular solution curve helps students understand real-world modeling where systems have specific starting states. Without a defined beginning point, a model would yield many mathematically possible behaviors, but only one corresponds to the actual scenario. In slope fields, this idea becomes concrete: the particular solution curve visually represents the system’s unique evolution from its initial condition.