Recognizing Separable Differential Equations

A separable differential equation can be rewritten so that expressions involving the dependent variable appear on one side and expressions involving the independent variable appear on the other, enabling direct integration.

Understanding the Structure of Separable Differential Equations

A separable differential equation is a first-order differential equation whose form allows it to be manipulated so each variable is isolated on its respective side of the equation. This structural feature is essential because the method of separation of variables requires integrating with respect to each variable independently. Students should focus on whether the derivative expression can be factored or rearranged into a product of a function of the dependent variable and a function of the independent variable.

A separable differential equation typically begins in the form $\frac{dy}{dx} = f(x, y)$.

The question is whether $f(x, y)$ can be expressed as a product of two single-variable functions, such as $g(x)h(y)$. If this is possible, then the differential equation is separable.

Identifying Dependent and Independent Variables Before Separation

To determine whether an equation is separable, students must be clear about which variable is dependent and which is independent. In AP Calculus AB contexts, the dependent variable is commonly $y$, and the independent variable is commonly $x$, although sometimes the variables may represent quantities such as population and time, velocity and distance, or temperature and time.

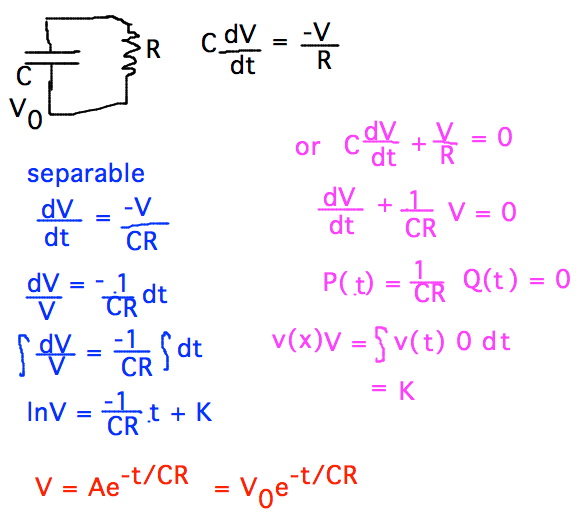
This figure shows a discharging capacitor modeled by the differential equation $C\frac{dV}{dt} = -\frac{V}{R}$, which can be rewritten in separable form. The voltage $V$ serves as the dependent variable while time $t$ is the independent variable, mirroring the roles discussed in the notes. Some solving steps appear in the image, extending slightly beyond the recognition stage of separability. Source.

Recognizing the variables properly ensures that the equation is manipulated in a meaningful and mathematically consistent way during the separation process.

By correctly identifying the variables, students can check whether each portion of the differential equation aligns with the appropriate differential expression ($dy$ or $dx$).

Structural Features That Make an Equation Separable

A differential equation is separable when its derivative expression can be reorganized as a product of single-variable components. This structure can appear in several recognizable forms:

Common patterns that indicate separability

• Product form: If $\frac{dy}{dx} = g(x)h(y)$, the equation is directly separable.

• Quotient form: If $\frac{dy}{dx} = \frac{g(x)}{h(y)}$, one can rearrange to isolate $h(y)dy$ and $g(x)dx$.

• Factored derivative expressions: If the right-hand side can be algebraically factored into separate $x$-dependent and $y$-dependent pieces, separability holds.

• Implicitly separable expressions: If expressions appear mixed, algebraic manipulation—such as factoring, expanding, or simplifying—may reveal separability.

Between these forms, the unifying characteristic is that each variable can ultimately be placed on a single side of the equation without mixing.

Situations That Require Care When Checking for Separability

Not every differential equation is separable, and it is important for students to distinguish truly separable cases from those that merely appear separable at first glance. A right-hand side expression involving $y + x$ or $xy + x$ may or may not be separable depending on whether it can be rewritten as a product of single-variable functions. Algebraic attentiveness helps prevent misclassification.

Situations that may require additional algebra

• Expressions involving sums, such as $x + y$, are not separable because they cannot be split into a product of purely $x$-dependent and $y$-dependent factors.

• Multiplicative expressions, such as $x(y^2 + 1)$, are separable because the entire $y$-dependent component can be grouped with $dy$.

• Rational expressions, such as $\frac{x^2}{3y - 1}$, are separable because the numerator and denominator depend on different variables in a way that can be isolated with multiplication.

Students should analyze whether rearrangement is algebraically possible rather than assuming separability from surface appearance.

How Separable Form Links to the Integration Process

Recognizing separability is the essential first step in solving such equations using the method of separation of variables. Once the equation has been rewritten appropriately, the next step is antidifferentiation. While this subsubtopic focuses only on recognizing separability, it is helpful to understand the general structure that results from a successful separation.

Having the differential equation in this form confirms that it is separable and prepares the equation for integration in later subsubtopics.

This infographic highlights the defining structure of a separable differential equation by displaying $\frac{dy}{dx} = g(x)h(y)$ and its separated counterpart $\frac{1}{h(y)},dy = g(x),dx$. The visual reinforces the idea that each variable must appear only with its associated differential. The text below the boxes briefly mentions general and particular solutions, which extend beyond the recognition step addressed in this subtopic. Source.

Practical Indicators of Separable Equations in AP Problems

AP Calculus AB typically uses differential equations that are straightforward to separate once the structure is recognized. Students should look for consistent patterns that signal separability:

• A derivative equals a product or quotient of functions of different variables.

• A derivative equals an expression that becomes separable after factoring.

• A derivative contains rational expressions whose numerator and denominator depend on different variables.

• A derivative that can be manipulated so that each variable appears only with its own differential.

Developing fluency in spotting these patterns helps students quickly determine whether separation of variables is applicable in a given differential-equation context.