This subsubtopic explains how accumulation functions generate particular solutions to differential equations by combining an initial condition with the accumulated effect of a rate of change over an interval.

Accumulation Functions as Particular Solutions

Understanding the Structure of an Accumulation Function

An accumulation function represents a quantity that changes over time according to a given rate function, while also starting from a specified initial amount. When a differential equation describes the rate at which a quantity varies, an accumulation function incorporates that rate to build an explicit formula for the particular solution satisfying a known initial condition. This structure allows students to connect a given derivative directly to a solution expression rooted in integration.

A key feature of accumulation functions is that they inherently encode the initial condition. Because the definite integral represents net accumulation from a lower bound, replacing this bound with the initial value ensures the resulting function fits both the differential equation and the initial point.

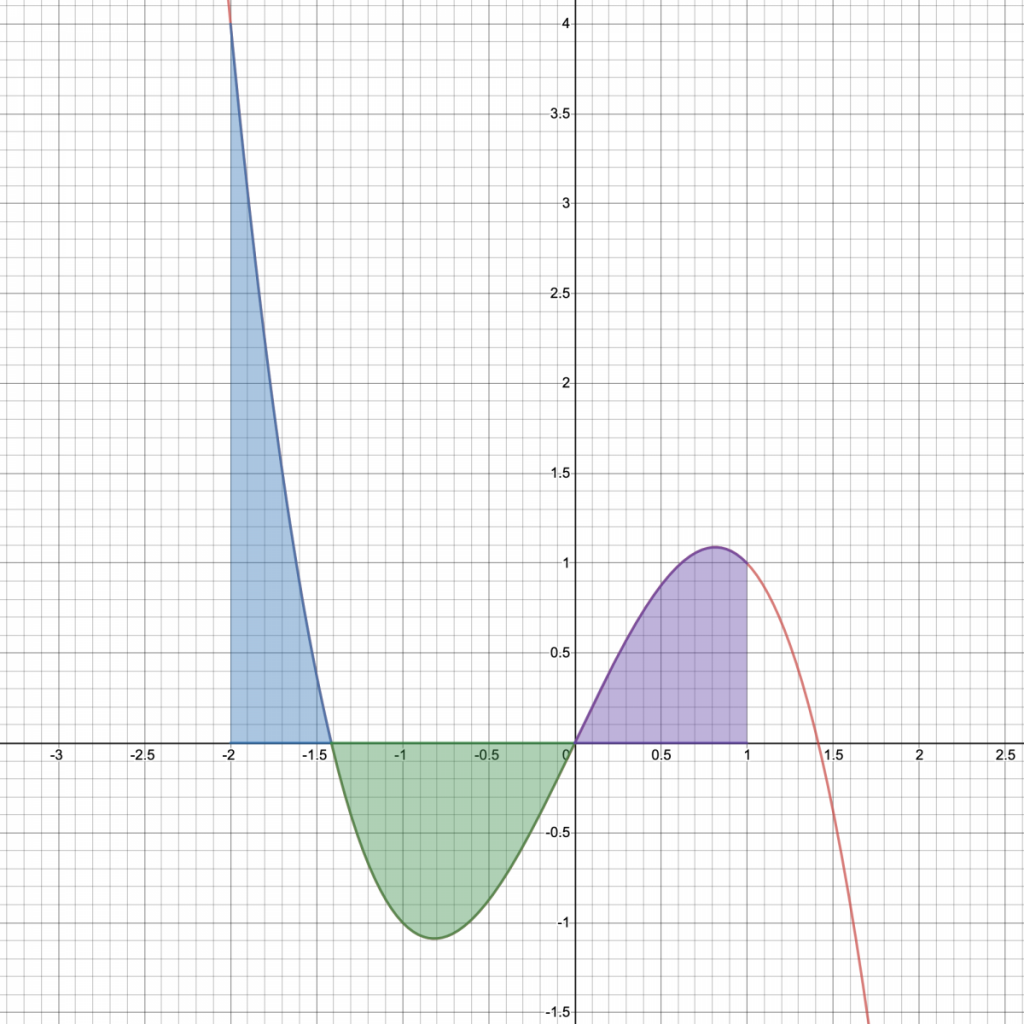
A graph of a function $f(x)$ with three shaded regions shows how a definite integral adds positive signed area above the x-axis and subtracts negative area below it, producing net accumulation. The blue and purple regions contribute positively to $\int_a^x f(t),dt$ while the green region contributes negatively. This illustrates how accumulation functions track total change rather than geometric size alone. Source.

Why Accumulation Functions Produce Particular Solutions

A differential equation such as $dy/dx = f(x)$ describes how a quantity changes but does not uniquely determine the quantity itself without additional data. A general antiderivative of the rate function includes an arbitrary constant, representing a family of general solutions. However, if an initial condition $y(a) = y_{0}$ is provided, an accumulation function removes uncertainty by selecting the correct constant automatically.

This is achieved through the structure
$F(x) = y_{0} + \int_{a}^{x} f(t), dt$,
which produces a value equal to $y_{0}$ when $x = a$ and then grows or decreases according to the integral of the rate function. This framework ensures that the resulting function satisfies all required components of a particular solution.

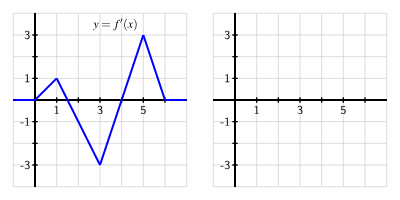
The left graph shows a rate function $f(t)$, while the right graph depicts its accumulation function $A(x)=\int_0^x f(t),dt$. Each x-value on the right represents total signed accumulation from the start, demonstrating how an integral produces a specific solution curve. This mirrors the structure of $F(x)=y_0+\int_a^x f(t),dt$ used to form particular solutions. Source.

The use of a definite integral rather than an indefinite one is essential, because the definite integral generates a single, specific function rather than a family of functions differing by a constant.

Connection to Differential Equations

Accumulation functions are tightly linked to differential equations through the Fundamental Theorem of Calculus, which states that the derivative of an integral of a continuous function returns the original integrand. This theorem guarantees that differentiating
$\int_{a}^{x} f(t), dt$
yields $f(x)$, confirming that $F'(x) = f(x)$ and ensuring the accumulation function satisfies the differential equation. The combination of initial value and integral ensures that both the differential relationship and the initial condition are met seamlessly.

Between the initial value and accumulated rate information, the accumulation function represents the precise behavior of the dependent variable from the starting point onward.

Interpreting Accumulation Functions in Modeling Contexts

Accumulation functions communicate how a quantity evolves in response to a rate. In many applied situations, the dependent variable changes in a way that can be viewed as accumulating or aggregating the effects of a rate process. Students should interpret an accumulation function in terms of:

• Starting value: the known amount at the beginning of observation.

• Rate function: the instantaneous rate of change that determines how the quantity grows or diminishes.

• Total accumulated change: the integral representing all changes from the initial point up to a given input.

These interpretations reinforce that accumulation functions not only produce a mathematically correct particular solution but also provide meaningful insight into real-world processes. Because every term in the accumulation function corresponds to specific contextual information, the resulting function is both mathematically valid and easily interpretable.

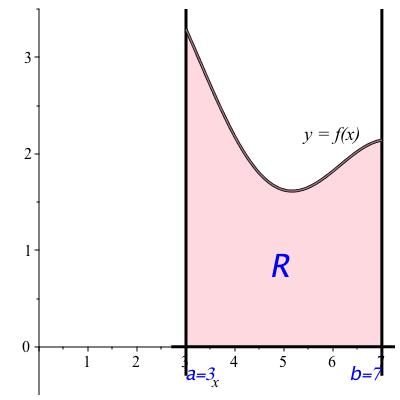
This figure shows the region under $f(x)$ between $x=a$ and $x=b$, representing the definite integral $\int_a^b f(x),dx$. The shaded area visualizes the accumulated effect of the rate function over that interval. Although it omits the initial value $y_0$, it directly illustrates the geometric component of accumulation functions in $F(x)=y_0+\int_a^x f(t),dt$. Source.

Key Properties and Structural Features

To use accumulation functions effectively, students should understand several consistent features:

• They always satisfy the given initial condition exactly.

• They use definite integrals, which automatically incorporate the correct constant of integration.

• They reflect the net change in the quantity, accounting for increases and decreases depending on the sign of the rate function.

• They provide a unique particular solution for a first-order differential equation with a specified initial value.

• They reinforce the relationship between integration and differentiation, demonstrating how a rate rebuilds the underlying function.

Process for Constructing an Accumulation Function

Students can follow a clear process to form a particular solution using an accumulation function:

• Identify the differential equation in the form $dy/dx = f(x)$.

• Determine the initial condition $y(a) = y_{0}$.

• Express the solution as the initial value plus the definite integral of the rate:

  • $F(x) = y_{0} + \int_{a}^{x} f(t), dt$.

• Verify that the function meets both the initial condition and the differential equation.