Interpreting Particular Solutions in Context

A particular solution describes one specific modeled situation, and interpreting it requires understanding how the function, its derivative, and the initial condition each convey meaningful information about real-world behavior.

Understanding the Role of a Particular Solution

A particular solution is a single function that satisfies both a differential equation and a given initial condition. When analyzing such a solution in context, students focus on how each mathematical component corresponds to a physical, biological, economic, or other real situation. Interpreting solutions goes beyond symbolic manipulation; it involves connecting the model’s structure to its narrative meaning.

Differential Equations and Modeled Quantities

A differential equation expresses how one quantity changes with respect to another. In context, the dependent variable typically represents a measurable quantity such as population size, temperature, velocity, or chemical concentration. The independent variable often represents time, though it may also represent distance or another relevant factor. The associated particular solution reveals the unique trajectory of the modeled system implied by the initial condition.

Following this interpretation, the derivative describes how the dependent variable responds instantaneously to changes in the independent variable according to the model’s rules.

Components of Interpretation

When interpreting a particular solution in a real-world scenario, students must articulate the meaning of three structural elements: the function, its derivative, and the initial condition. Each corresponds to different aspects of the modeled behavior.

The Function as a Representation of the Quantity

The particular solution function gives the exact value of the modeled quantity for any permissible value of the independent variable. Interpreting it involves connecting the algebraic expression to the described behavior.

• The function represents the state of the system at every moment or location.

• The domain identifies when or where the model applies.

• The structure of the formula conveys whether the quantity grows, decays, oscillates, or stabilizes.

From this starting value, the function shows how the modeled system evolves over time or through another dimension.

Interpreting the Derivative

The derivative communicates the rate of change of the quantity. In modeling, rate information is central because it describes how the system responds dynamically.

• A positive derivative indicates increasing behavior in the modeled quantity.

• A negative derivative signals decreasing behavior.

• The magnitude of the derivative expresses how rapidly the quantity changes.

Interpreting this relationship requires describing how specific influences or constraints within the context shape the behavior of the rate.

A sentence here clarifies how the derivative and function jointly describe the system’s evolution rather than isolated pieces of mathematical notation.

Initial Condition in Context

The initial condition anchors the model to a specific real-world measurement. It ensures the solution corresponds to the situation described rather than any other theoretically possible scenario.

Important considerations include:

• Identifying what the given point means physically.

• Determining how the initial measurement influences all future values predicted by the model.

• Recognizing that changing the initial condition changes the particular solution.

Using Context to Interpret Behavior

Interpretation involves explaining what the model predicts rather than computing numbers. Students focus on the qualitative meaning of the particular solution.

Key interpretive tasks include:

• Explaining what the function’s output signifies for the real system.

• Describing how the dependent variable behaves as the independent variable increases.

• Connecting parameter values to contextual meaning, such as growth rates or limiting behavior.

• Using the structure of the particular solution to reason about long-term outcomes, turning points, or stabilization patterns.

A contextual interpretation emphasizes narrative description rather than symbolic manipulation.

How to Read a Particular Solution Meaningfully

When given a particular solution, students should approach interpretation systematically:

Identifying What the Variables Represent

Understanding begins by mapping symbols to quantities. A variable without context lacks real meaning, so an essential step is restating what $x$ and $y$ represent.

Connecting the Function Form to Behavior

Students should articulate how the algebraic form affects understanding. For example, exponential expressions suggest proportional growth or decay, while rational or logistic forms may indicate limiting behavior.

Describing Real-World Implications

Interpretation often includes:

• Statements about increasing or decreasing behavior.

• Conditions under which the quantity grows slowly or rapidly.

• Explanations of what happens as the independent variable becomes large.

• Insights into how changes in parameters reshape the model’s predictions.

Using the Initial Condition to Frame the Scenario

The initial condition provides a grounding point that situates the entire model. Students should explain what the starting value represents and how it influences the entire solution curve.

Each initial condition corresponds to a unique solution curve that we can imagine tracing on a graph of the dependent variable versus the independent variable.

This diagram displays a slope field and one integral curve that follows the direction of the field. The curve represents a particular solution consistent with the differential equation’s prescribed slopes. Although slope fields belong to another subtopic, here they illustrate how a particular solution remains tangent to each indicated slope. Source.

Synthesizing Function, Derivative, and Initial Condition

Interpreting particular solutions requires recognizing that the function, its rate of change, and the initial value form a coherent narrative. Together they describe not only where a system begins but how and why it evolves according to the differential equation governing it.

For example, if $y(t)$ gives the size of a population, $y(0)$ is the initial population and $y'(t)$ gives the instantaneous rate at which individuals are being added per unit time.

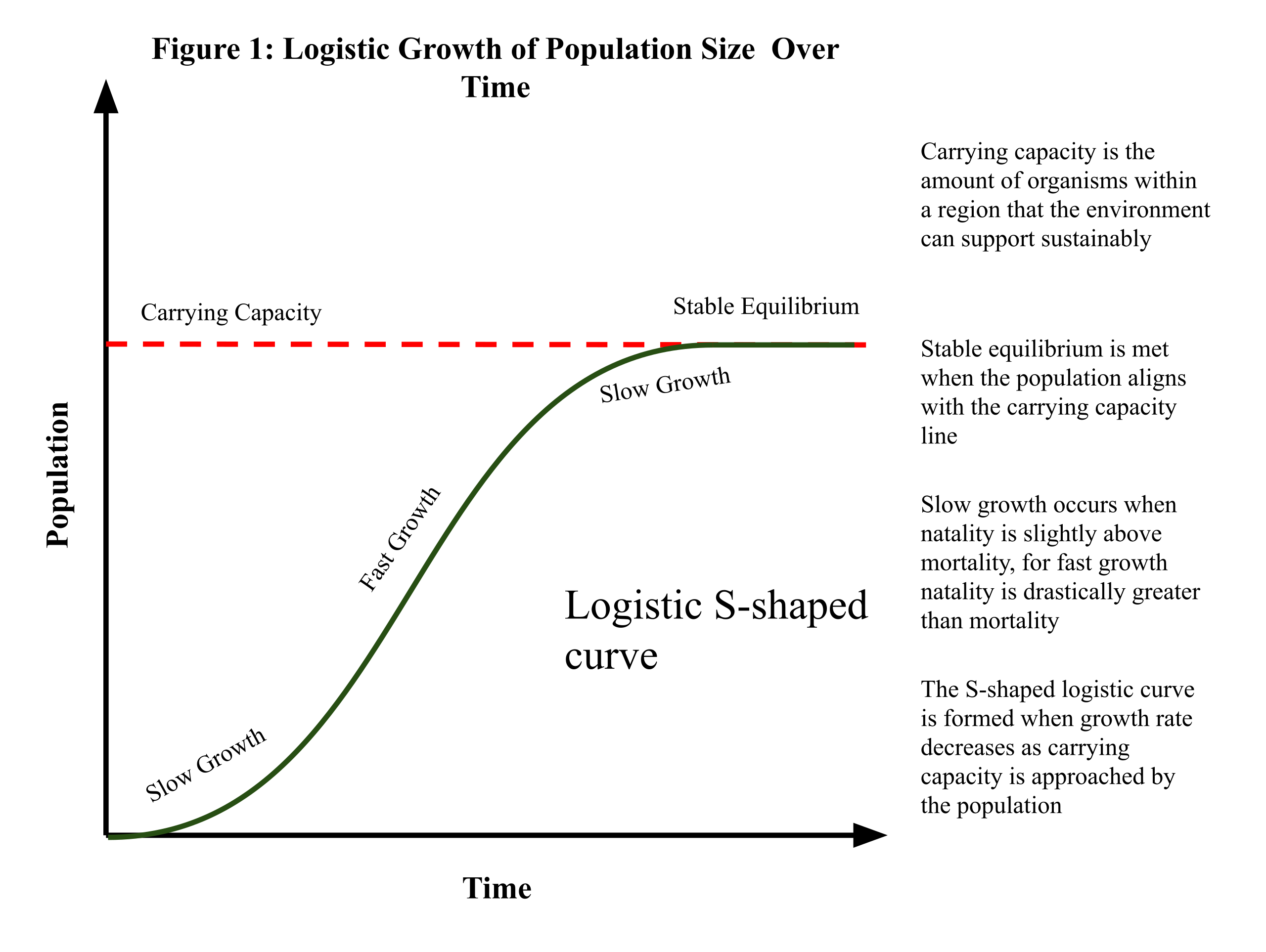
This graph shows an S-shaped logistic curve representing a population $P(t)$ that increases over time and approaches a carrying capacity. The curve is a particular solution determined by an initial population. The explicit carrying-capacity marking exceeds AB scope but helps illustrate contextual interpretation of long-term modeled behavior. Source.