Initial conditions allow us to convert a general antiderivative with an arbitrary constant into a unique particular solution that reflects a specific situation described by the differential equation.

Using Initial Conditions to Determine Constants

When solving a first-order differential equation through antidifferentiation or separation of variables, the result is typically a general solution containing an arbitrary constant. This constant represents an entire family of functions that satisfy the differential equation. To identify the single function relevant to a given context, we use an initial condition, which specifies the value of the dependent variable at a particular value of the independent variable.

Understanding the Role of Initial Conditions

An initial condition is a statement that gives one point $(x_0, y_0)$ on the solution curve. It ensures the model aligns with the specific scenario being described. Because many differential equations allow infinitely many antiderivatives, the initial condition selects the only member of the family that passes through the given point.

The presence of an initial condition links the general mathematical relationship to the physical or contextual situation being modeled, such as population at time zero or velocity at a specific moment.

Structure of General Solutions

When solving a differential equation such as $dy/dx = f(x,y)$, antidifferentiation produces an expression that includes an arbitrary constant $C$. This constant appears because differentiation removes constant information, leaving an entire family of antiderivatives.

Family of parabolas of the form $y = x^2 + a$ for various values of the parameter $a$. The curves illustrate how a general solution like $y = F(x) + C$ represents many possible functions. An initial condition selects exactly one curve from this family. Source.

A single sentence separating blocks: This general form illustrates the need for further information to identify a specific function.

How Initial Conditions Produce a Particular Solution

To move from the general solution to a particular solution, we substitute the values from the initial condition into the general form and solve for $C$. This step anchors the curve to the exact point required by the context.

The Process of Applying an Initial Condition

Students must understand the precise sequence used to determine the constant of integration:

• Begin with the general solution obtained from integrating the differential equation.

• Substitute the given values of the independent and dependent variables from the initial condition.

• Solve the resulting equation for the constant $C$.

• Substitute the determined value of $C$ back into the general solution to form the particular solution.

• Express the resulting function clearly, ensuring it satisfies both the differential equation and the initial condition.

The resulting expression is the unique function that fits the specified situation.

Meaning and Interpretation of the Constant

Although the constant $C$ may appear purely algebraic, it has meaningful implications. In many contexts, it encodes initial states such as initial population, initial temperature, or starting position of an object. The value of $C$ tells us how the modeled system begins at the designated point and ensures the solution curve reflects that starting state.

One sentence between blocks: This definition reinforces how the arbitrary constant is eliminated in order to describe a specific model outcome.

Importance in Mathematical Modeling

Differential equations describe how quantities change, but without initial conditions the descriptions are incomplete. Only after applying the given point do we obtain a solution that corresponds to a real measurement or observed value. In applied settings, the initial condition often represents a baseline measurement, such as the amount of a substance at time zero or the height of fluid in a tank at the start of an experiment.

Common Situations Involving Initial Conditions

In AP Calculus AB contexts, initial conditions are typically provided in one of the following ways:

• A statement like “when $x = a$, $y = b$,” written symbolically as $y(a) = b$.

• A contextual description specifying a starting time or initial measurement.

• A graph or slope field showing the solution must pass through a particular point.

Across these situations, the purpose remains the same: pin down the correct member of the solution family.

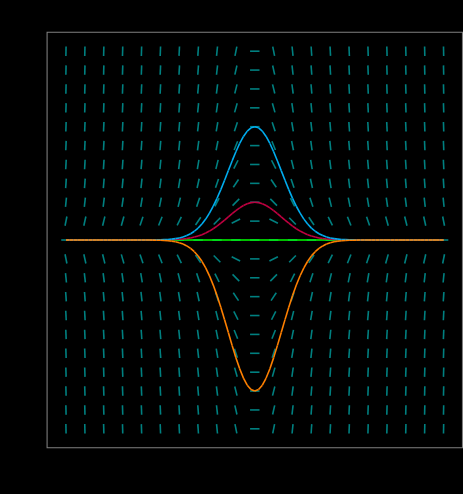
Direction field with multiple solution curves for a first-order differential equation. Each curve shows a different solution corresponding to a different initial condition. Although the diagram contains more detail than required by the syllabus, it clearly illustrates how an initial value selects one unique solution from many. Source.

Ensuring Consistency with the Differential Equation

After determining the particular solution, it is essential to verify that the resulting function satisfies both the differential equation and the initial condition. This reinforces mathematical accuracy and emphasizes the interconnected roles of derivatives, antiderivatives, and conditions supplied by the problem context.

By understanding how initial conditions allow us to determine constants, students gain a clearer view of how differential equations produce meaningful, situation-specific solutions within the framework of AP Calculus AB.