The average value of a function provides a meaningful way to describe a function’s overall behavior across an interval by combining accumulated change with interval length to produce a representative output.

Understanding the Average Value Formula

The concept of the average value of a continuous function arises naturally when examining how a function behaves over a closed interval. Instead of sampling individual points, the formula incorporates every value the function takes through integration, ensuring that the average reflects the entire continuous curve rather than isolated observations. This approach mirrors familiar ideas of averaging numerical data, but adapts the idea to continuous settings where infinitely many values contribute to the result.

Why the Integral Appears

The definite integral measures accumulated value over the interval $[a,b]$. In this context, accumulated value represents the total area under the curve of $f(x)$ above the x-axis or net signed area when the graph dips below the axis. Dividing this accumulated value by the interval length produces a single number that acts as a representative “height” of the function across the interval.

The Average Value Formula

To formalize the idea of a representative height, we define the average value using a widely taught formula that applies to any continuous function on a closed interval.

This expression ensures that the average value represents exactly the constant height a rectangle over $[a,b]$ would need to have to match the area under $f(x)$.

A sentence must appear here to ensure appropriate spacing before any subsequent definition or equation blocks appear.

The average value $f_{\text{avg}}$ is the constant height such that the rectangle with base $[a,b]$ and height $f_{\text{avg}}$ has the same area as the region under $f$.

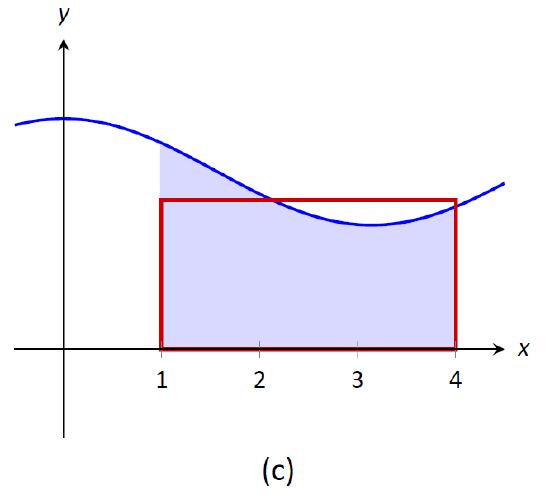
A continuous function is graphed on $[1,4]$ with the area under its curve shaded. A red rectangle with base $[1,4]$ and a carefully chosen height has exactly the same area as the shaded region, so its height represents the average value of the function on that interval. This visual reinforces the formula $f_{\text{avg}} = \dfrac{1}{b-a}\int_a^b f(x),dx$. Source.

Meaning of the Components

Each part of the formula has a clear interpretation rooted in integral calculus:

• The definite integral captures the total accumulated output of the function over the interval.

• The interval length, $b-a$, represents how wide the region of interest is.

• Dividing accumulated value by interval length transforms a total quantity into an average rate or level.

This mirrors average calculations in everyday contexts, such as average speed, where total distance is divided by total time.

When the Formula Applies

The formula for the average value requires that the function be continuous on the interval. This requirement ensures that the definite integral is well-defined and that the function has no jumps or undefined points. AP Calculus AB emphasizes this continuity condition because it guarantees that every part of the function contributes smoothly to the accumulated value.

Situations Where the Formula Is Useful

Students encounter the average value formula in many types of problems, including:

• Estimating representative function heights, such as average temperature or concentration.

• Comparing actual values to typical behavior, especially when determining whether a function rises above or falls below its average level on subintervals.

• Modeling physical quantities, such as average velocity or average rate of flow, when the underlying variable changes continuously over time.

Interpreting the Integral as Accumulated Value

A central idea in AP Calculus AB is understanding a definite integral as accumulation. In the context of average value:

• The definite integral gathers all instantaneous values of the function across the interval.

• Lower parts of the graph contribute less to the integral; higher parts contribute more.

• The final accumulated quantity reflects the combined effect of the entire function over the interval.

This accumulation perspective is essential for interpreting what the average value means beyond the algebraic formula.

Conceptual Interpretation of Average Value

The average value represents the constant function height that would generate the same accumulated value as $f(x)$ over the interval. Visualizing this constant-height rectangle is helpful, as it conveys the idea that the average value smooths out the peaks and valleys of the actual graph.

Key Ideas to Remember

• The average value is not the midpoint value $f!\left(\frac{a+b}{2}\right)$; it is derived from the entire interval.

• Areas below the x-axis decrease the accumulated value, since the definite integral accounts for signed area.

• The formula gives a single summary number describing the function’s overall behavior on the interval.

Process for Finding Average Value

Students can use the formula efficiently by following a consistent method:

• Identify the interval $[a,b]$ on which the average value is to be computed.

• Confirm that $f(x)$ is continuous on this interval, ensuring integrability.

• Compute or estimate the definite integral $\int_a^b f(x),dx$.

• Multiply by the reciprocal of the interval length, $\frac{1}{b-a}$.

• Interpret the result in the context of the problem, focusing on what the average level represents.

These steps reflect the AP emphasis on connecting integrals with accumulated change and interpreting the meaning of results.

By the Mean Value Theorem for Integrals, there is at least one point $c$ in $[a,b]$ where $f(c)$ actually equals this average height.

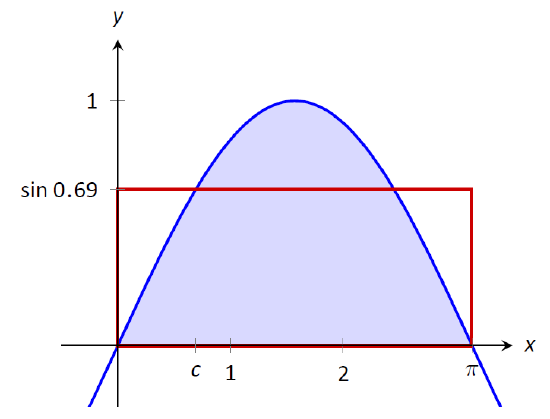
The graph of $y=\sin x$ on $[0,\pi]$ is shown with the area under the curve shaded. A red rectangle of height $\sin(0.69)$ has the same area as the shaded region, so this height is the average value of $\sin x$ on the interval. The marked point $c$ shows a location where the function’s value matches this average height, illustrating the Mean Value Theorem for Integrals. Source.

Interpreting the Formula in Applied Settings

In real-world applications, the average value formula enables students to describe an average level, rate, or quantity across a time or input interval. For example, if $f(x)$ models a rate of production, then the average value describes the typical production rate over that period. Because the definite integral expresses accumulated change, the final average connects a total quantity with the duration or span over which it was recorded.