The average value of a function is a central idea in integral calculus, and this subsubtopic focuses on learning to compute it using formulas, tables, or graphical information. These notes develop the essential skills needed to interpret and apply the average value formula across multiple representations of functions.

Understanding the Task of Computing an Average Value

Students must be able to compute the average value of a continuous function on an interval by combining information from formulas, tables, or graphs with the definite integral that represents accumulated change. Calculating an average value requires identifying the interval, determining the integral of the function over that interval, and applying the appropriate mathematical structure based on the representation given.

The Role of Accumulated Change

The computation of an average value connects deeply to the idea that integration measures accumulated change over an interval. When the function is known explicitly, when discrete data approximates the function, or when the function is presented visually, the goal remains to obtain a reliable expression or estimate for this accumulation. This accumulated quantity is then normalized by the interval length to produce the average.

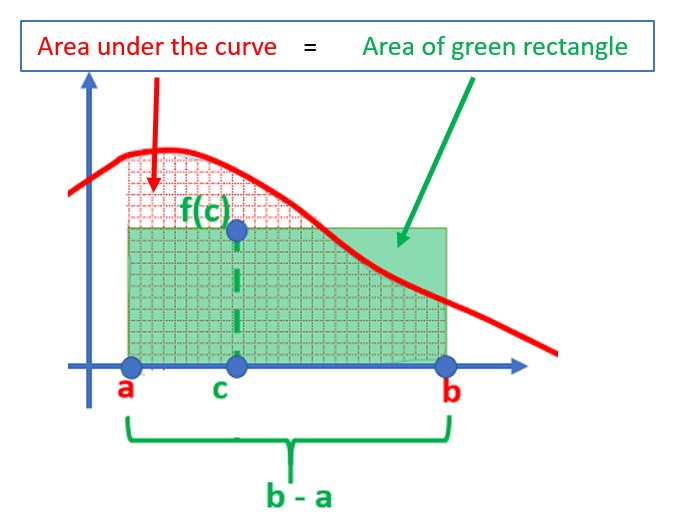
This diagram illustrates a function on $[a,b]$ and a rectangle of height $f(c)$ whose area matches the integral of the function. It visually demonstrates how the average value corresponds to the height of a constant function with equal accumulated area. The surrounding discussion of the Mean Value Theorem for integrals extends beyond the syllabus, but the geometric representation of average value is directly relevant. Source.

The Average Value Formula

The concept of average value relies on a consistent mathematical expression that applies to all representations.

At its core, the integral computes the total accumulated value, and the factor $\frac{1}{b-a}$ rescales the result so that it matches the interpretation of a mean level of the function on the interval. This formula is the foundation for calculations across formulas, tables, and graphs.

A normal sentence is placed here to provide separation before any further structured blocks.

Calculating Average Value from Formulas

When the function is given by an explicit algebraic rule, the process emphasizes symbolic evaluation.

Key Process When Using Formulas

• Identify the interval [a,b][a,b][a,b] from the prompt.

• Integrate the function over that interval using appropriate antiderivative techniques.

• Apply the average value formula by dividing the definite integral by the interval length.

• Interpret the value as the typical height of the function on that interval.

This approach requires fluency with integration rules and careful evaluation of definite integrals. Students should focus on recognizing integrands that allow direct antiderivatives and those that may require rewriting or substitution when appropriate at the AP Calculus AB level.

Emphasizing Conceptual Understanding

Even when formulas allow exact computation, the resulting average value is more than a numerical result. It represents the constant value that the function would need to maintain across the interval to match the actual accumulated amount. Highlighting this concept helps students connect algebraic manipulation with graphical meaning.

Calculating Average Value from Tables

Tables require students to approximate integrals rather than compute them exactly. The definite integral is interpreted numerically using the available data.

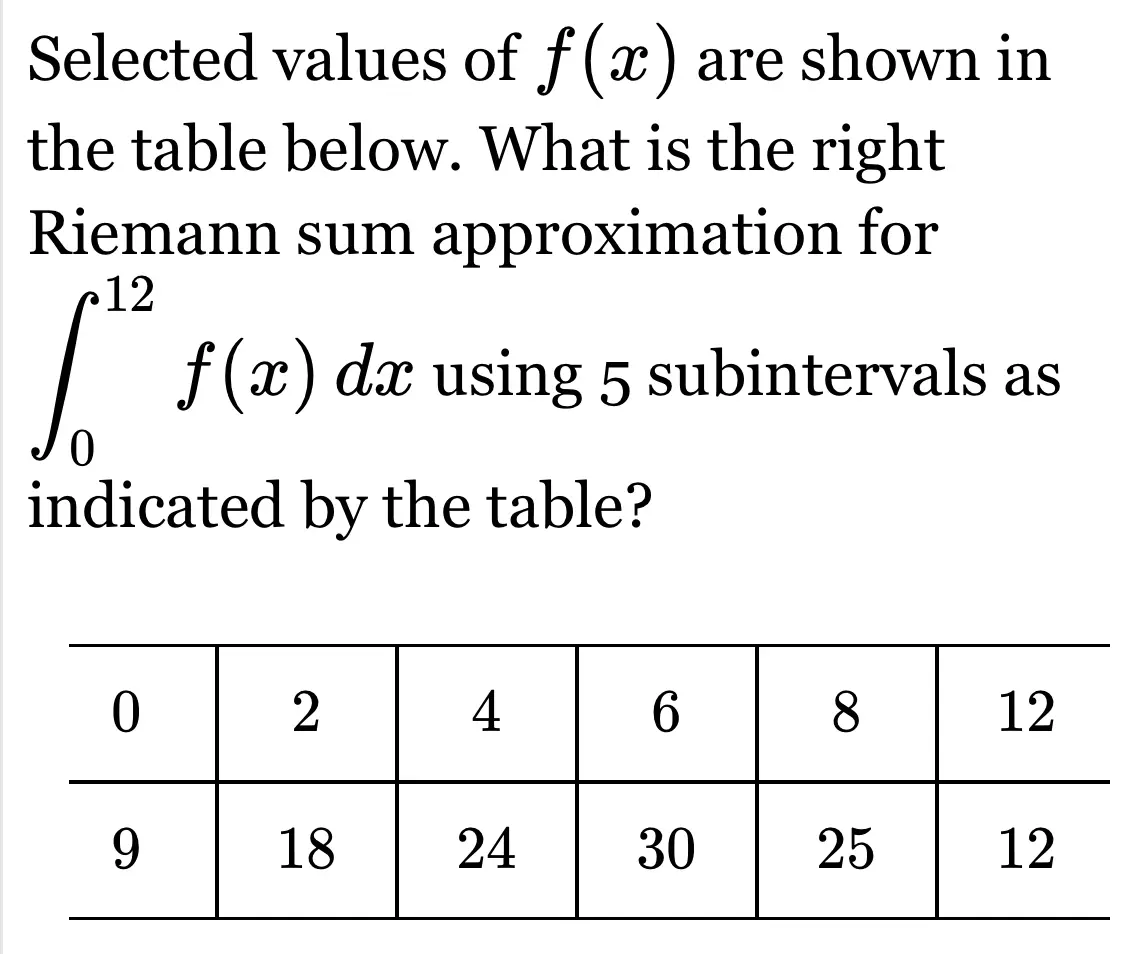
This table provides discrete values of a function at selected points, allowing approximation of $\int_a^b f(x),dx$ using a Riemann sum. It mirrors the structure of AP-style problems requiring numerical estimation from tables. The prompt above the image refers to a right Riemann sum for $\int_0^{12} f(x),dx$, which is slightly more specific than the syllabus requires but uses the same underlying accumulation idea. Source.

Strategies for Using Tabular Data

• Determine the interval spanned by the table entries.

• Use numerical methods such as left-endpoint, right-endpoint, or trapezoidal approximations to estimate the definite integral.

• Insert the estimated integral into the average value formula to obtain the approximate average.

• Assess the quality of the estimate based on the density and regularity of the table values.

Because tables provide discrete snapshots of the function rather than a full analytic expression, students must think in terms of accumulation through approximations. The goal is to produce a faithful estimate consistent with AP expectations, using standard numeric techniques introduced in prior units.

Recognizing Behavior from Tables

Even without an explicit graph, tables can suggest whether a function is increasing, decreasing, oscillating, or changing gradually. This qualitative information supports better interpretations of the resulting average value, framing it within the approximate behavior of the function.

Calculating Average Value from Graphs

Graphical information requires interpreting the definite integral as area under a curve, paying attention to the geometry of the region and the overall shape of the function.

Visual Interpretation Strategies

• Identify the interval boundaries on the horizontal axis.

• Determine whether the function lies above or below the axis, since signed area affects the integral.

• Break the region into geometric shapes, such as rectangles, triangles, or trapezoids, when possible.

• Use numerical or geometric estimates to determine the value of the definite integral.

• Apply the average value formula by dividing by the interval length.

In many graph-based problems, the integral cannot be computed exactly but must be estimated visually. Students should rely on geometric reasoning and proportionality, especially when only approximate coordinates are available.

Distinguishing Average Value from Area Alone

The integral computed from the graph represents accumulated signed area. The average value divides this accumulation over the interval, creating a quantity that represents the average height of the function. Emphasizing this distinction helps prevent the common misconception that the integral itself is the average.

Connecting Different Representations of the Same Process

Regardless of whether information is given via formula, table, or graph, the goal is always to compute or estimate the definite integral of the function and then apply the scaling factor $\frac{1}{b-a}$. Students should focus on recognizing the underlying structure of the problem rather than the surface representation. Patterns in accumulation remain consistent across representations, reinforcing the unifying nature of the average value concept in calculus.