Average value provides a meaningful way to interpret a function’s overall behavior across an interval, summarizing continuously changing quantities with a single representative level.

Interpreting Average Value in Applied Settings

Understanding the average value of a function is central to connecting definite integrals with real-world quantities. In applications, the average value represents the typical level of a variable across an entire interval, even when the function changes at every moment. Because many real contexts involve continuously varying rates—such as velocity, temperature, concentration, or power output—the average value provides clarity about the system’s overall behavior rather than its instantaneous fluctuations.

When a function models a physical or contextual quantity, integrating it accumulates the total amount of that quantity over an interval. Dividing this accumulated total by the interval length produces a single number that can be interpreted as the average level of the changing quantity.

The average value contrasts with instantaneous values, which may spike or dip. Real-world interpretation emphasizes that the average value is not necessarily attained by the function but summarizes its overall trend across the interval.

Graphically, the average value corresponds to a horizontal line whose constant height produces the same area as the region under $f$ on $[a,b]$.

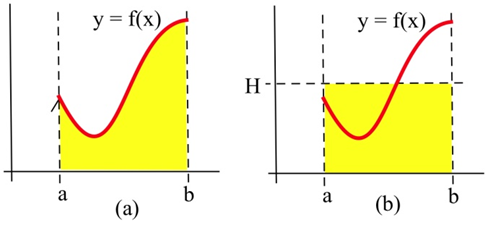
A continuous function $f(x)$ on $[a,b]$ is shown with the area under its graph shaded, beside a rectangle of width $b-a$ and height $H$. The two shaded regions have the same area, illustrating that the average value is the constant height $H$ giving the same total accumulation as the original varying function. The labels and structure slightly exceed AP AB requirements but remain fully aligned with the underlying concept. Source.

Why the Average Value Matters in Applications

Relating Accumulated Change to Typical Behavior

Many applied contexts involve measuring or predicting how a quantity accumulates over time. The integral models total accumulation, while the average value offers an interpretable statistic that answers the question: What constant level over the interval would produce the same total accumulation?

This makes average value especially useful for:

• Simplifying complex behavior into a single representative value

• Comparing different intervals or processes

• Interpreting physical measurements with fluctuating inputs

• Communicating results in understandable terms

In scientific and engineering environments, average levels often guide decisions more effectively than extreme or instantaneous values.

Key Interpretive Principles

Viewing the Average Value as a Constant Equivalent

In applied problems, students interpret the average value
$\frac{1}{b-a}\int_a^b f(x),dx$
as the height of a constant function on the same interval that accumulates the same total quantity. This interpretation connects directly to the geometric meaning of the definite integral as area under the curve.

Thus, average value may be understood as:

• A constant output that would produce equal accumulated effect

• A representative magnitude of an otherwise variable process

• A benchmark for comparing actual function behavior to a uniform scenario

Distinguishing Between Average Value and Average Rate of Change

The average value of a function differs fundamentally from the average rate of change.

Average value instead concerns the mean height of the function across an interval, requiring integration. Students should recognize that these two concepts serve different purposes in modeling and interpretation. A normal sentence is placed here before the next definition block.

Whereas average rate of change describes how fast something changes, average value explains how large the quantity tends to be across the interval.

Interpreting Average Value in Real-World Systems

The AP syllabus emphasizes interpreting average value in applied scenarios. Important interpretive themes include:

• Temporal Averages:

  • Average velocity over a trip

  • Average temperature over a day

  • Average rate of water flow through a pipe

• Spatial Averages:

  • Average pollutant concentration along a river segment

  • Average height of a curve across an interval in geometric modeling

• Operational Averages:

  • Average power usage by a machine

  • Average cost rate in economics

  • Average chemical reaction rate over time

In each case, the function represents a rate or level, while its integral represents total accumulation. The average value communicates the typical magnitude in a way that smooths out peaks and troughs and provides an accessible interpretation.

Linguistic Interpretation in Contextual Problems

When solving real-world problems, students should practice interpreting statements such as:

• “On average, the temperature was 68°F from noon to 6 p.m.”

• “The machine produced an average of 45 units per hour.”

• “The average pollutant concentration in the lake was 0.02 mg/L.”

These statements correspond directly to the mathematical meaning of average value:
$\frac{1}{b-a}\int_a^b f(x),dx$.
They describe a constant level that produces the same total effect as the variable function.

In a reservoir setting, $f_{\text{ave}}$ is the single water level that would produce the same total stored volume over the day as the actual fluctuating water level.

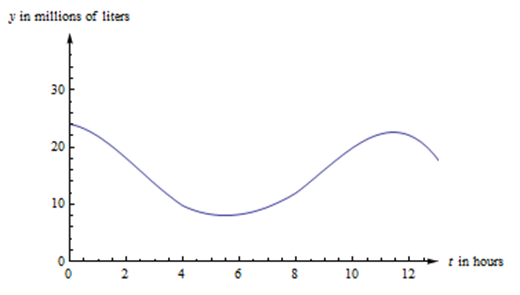
The graph shows reservoir volume $V(t)$ over a 12-hour interval, together with a horizontal line $y=15$ whose rectangular area matches the area under the varying volume curve. This constant level represents the average value, reflecting the uniform water level that would generate the same total stored volume. Numerical scales shown originate from the textbook example and exceed the AP requirement but illustrate the core idea clearly. Source.

Practical Interpretation Techniques

Students can follow several structured steps when analyzing average value in context:

• Identify the function representing the real-world quantity.

• Specify the interval over which the process occurs.

• Interpret the integral as total accumulation.

• Divide by interval length to obtain the average level.

• Explain the meaning in terms of the scenario, tying the result to a physical or contextual quantity.

These steps reinforce the idea that average value is a tool for summarizing complex functional behavior in applied contexts by providing a meaningful and interpretable constant equivalent.