The average value of a function plays a central role in understanding how quantities behave across intervals, providing a single representative value that reflects overall behavior.

Understanding the Concept of Average Value

The average value of a continuous function on an interval connects the idea of accumulation to a meaningful single number describing typical output. In AP Calculus AB, this subsubtopic emphasizes how the definite integral captures accumulated change and how this total accumulation, when distributed evenly over the interval length, yields an average.

When introducing the term average value of a function, it is essential to view it as a mathematical tool for describing the overall level of a varying quantity. Averaging a function is not simply sampling or taking midpoint values but instead relies on the total area under the curve.

This idea builds on the definite integral as a measure of accumulated output, where each infinitely thin slice contributes to the total. By relating accumulation to interval length, the average value offers insight into the function’s general behavior.

Why the Definite Integral Defines Average Value

A definite integral represents the accumulation of infinitely many small contributions of a function’s output. The average value is then determined by dividing this total accumulation by the interval width.

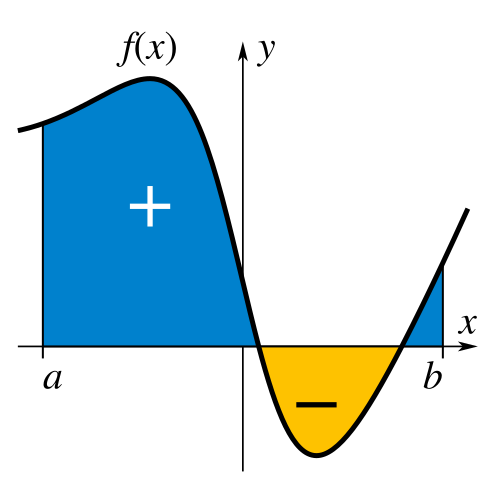
This figure illustrates a function whose signed areas above and below the $x$-axis represent positive and negative contributions to the definite integral $\int_a^b f(x),dx$. The shaded regions demonstrate how accumulated output is formed by combining these contributions. Although the image includes signed area, it supports understanding of accumulation, which underlies the definition of average value. Source.

This processed quantity functions as a constant value that, if maintained across the interval, would produce the same total accumulation as the original function.

Because the integral $\int_a^b f(x),dx$ represents accumulated change, dividing by $(b-a)$ yields a value that reflects a typical or representative output. This links accumulation to distribution and shows why the average value aligns with intuitive ideas of balance.

Understanding this relationship also clarifies how the average value differs from average rate of change. The latter measures change in output relative to change in input, while the average value measures the overall level of the output itself.

Interpreting Average Value Visually

Viewing graphs enhances conceptual understanding of average value. A graph of $f(x)$ over $[a,b]$ allows students to visualize the integral as the area under the curve.

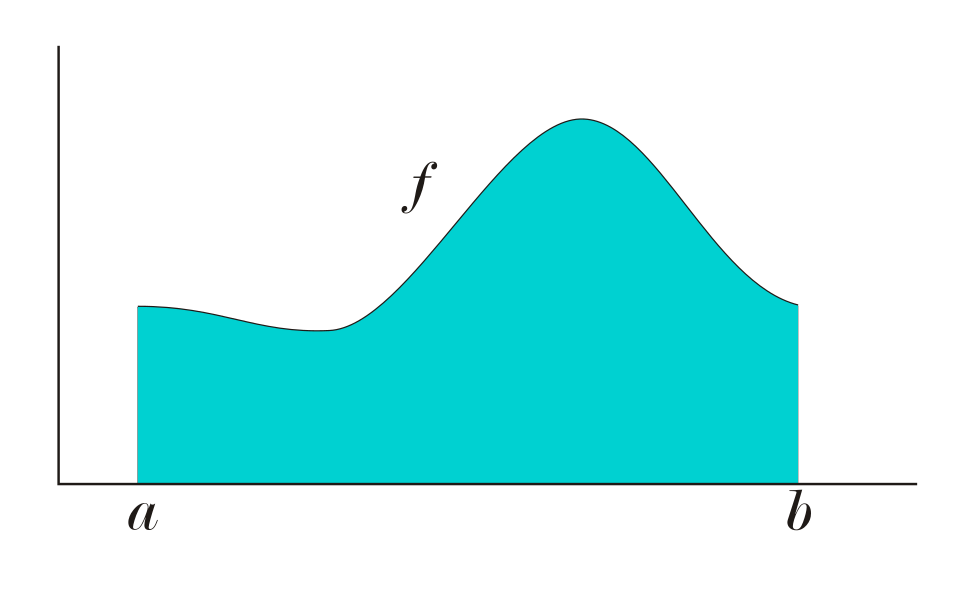
This figure depicts a function $f$ defined above the $x$-axis, with the shaded region representing the area corresponding to $\int_a^b f(x),dx$. The region shows how the integral measures total accumulated output over the interval. This accumulated area is what is evenly distributed across the interval length when determining the average value of the function. Source.

The average value corresponds to the height of a horizontal line whose rectangular area equals the area under $f(x)$ on the interval.

To interpret this visually, consider:

• The area under the curve represents the total accumulation of the function’s output.

• A rectangle spanning the same interval with height equal to the average value has identical area.

• The average value therefore serves as the constant height required to match the function’s accumulated output.

This interpretation connects algebraic and geometric thinking, reinforcing the role of the definite integral in describing accumulated quantities.

Conceptual Foundations and Key Properties

To fully understand the average value of a function, several conceptual foundations are useful:

Continuity Requirement

The function must be continuous on the closed interval $[a,b]$. This ensures the definite integral exists and accurately represents total accumulation.

Relationship to Accumulation

Average value is a direct application of the idea that integration accumulates infinitely many small contributions. Because accumulation is inherently linked to the rate-of-change structure of functions, the average value reflects how a function behaves collectively rather than locally.

Interpretive Meaning

The average value communicates the central tendency of the function’s values over an interval, serving as a meaningful descriptor in many contexts. Its interpretation relies on the integral as a measurement of how much output has been produced overall.

A key idea is that the average value may differ from any specific value the function takes. Unlike discrete averages, continuous averaging reflects infinitely many outputs, producing a theoretical construct representing overall behavior.

Connections to Future Topics

Although this subsubtopic focuses on the basic understanding of average value, it establishes groundwork for later applications involving accumulation, distribution, and real-world interpretation. The conceptual structure introduced here reappears in contexts such as motion, density, fluid flow, and other settings requiring accumulated quantities spread over intervals.

Key Points for Study

To reinforce understanding, students should become comfortable with the following:

• Viewing the definite integral as accumulated change.

• Interpreting average value as the accumulation divided by interval length.

• Recognizing that average value describes a representative height on a graph.

• Understanding the conditions that guarantee an average value exists.

• Distinguishing average value from related concepts such as average rate of change.

These ideas collectively support the AP Calculus AB requirement to interpret and use the average value of a function through the lens of definite integrals and accumulation.