AP Syllabus focus:
‘The definite integral of the particle’s speed, |v(t)|, over a time interval gives the total distance traveled, even when the velocity changes sign during the motion.’
Total distance traveled describes how far a particle moves along a line, regardless of direction, and is computed by integrating its speed, the magnitude of its velocity, over time.
Understanding Total Distance Traveled
Total distance traveled is a central idea in rectilinear motion because it measures the complete path length rather than the net change in position. While displacement captures how far a particle ends up from where it started, total distance accounts for all forward and backward movement. The AP syllabus emphasizes that integrating speed, written as , reliably accumulates distance even when the velocity becomes negative.
Term: Speed — The magnitude of velocity, written as , representing how fast an object moves regardless of direction.
When a particle changes direction, its velocity switches sign, but its speed remains nonnegative. Therefore, integrating speed ensures that every portion of motion contributes positively to accumulated distance.
Why Speed Must Be Used Instead of Velocity
Velocity represents both speed and direction. When velocity is integrated directly, negative values subtract from total accumulation, producing displacement, not distance. Total distance traveled must include all motion, so negative velocity values must be converted to their positive magnitude.
= Total length of the particle’s path on the interval
= Speed, always nonnegative
= Start and end times of the motion interval
This expression matches the syllabus requirement: the definite integral of speed gives total distance, fully accumulating movement wherever direction reversals occur.
A subtle but important aspect is recognizing when velocity changes sign. In many motion scenarios, the particle may move forward for part of the interval and backward for another. Integrating ensures that the backward part contributes positively to distance, maintaining conceptual consistency with physical travel.
Identifying Direction Changes in Motion
To correctly compute total distance, students must be aware of direction changes. These occur when the velocity equals zero, marking a turning point. Even without performing calculations in these notes, it is helpful to organize conceptual steps clearly.
Key Observations for Direction Changes
A velocity of zero signals a momentary stop or direction reversal.
A positive velocity indicates forward movement along the chosen axis.
A negative velocity indicates backward movement.
Each segment between sign changes contributes positively to total distance via .
These points help shape the way students think about motion graphs and tables, aligning with AP expectations.
Using Graphs, Tables, or Formulas to Determine Total Distance
The AP specification expects students to apply the total-distance idea across different representations. Regardless of representation, the conceptual process centers on accumulating the magnitude of velocity across the interval.
When Given a Formula for Velocity
Students can examine the velocity function to determine when it is positive, negative, or zero. This supports an understanding of direction changes and reinforces why speed must be used.
When Working with a Graph of Velocity
A velocity graph above the axis represents positive velocity, while portions below represent negative velocity.
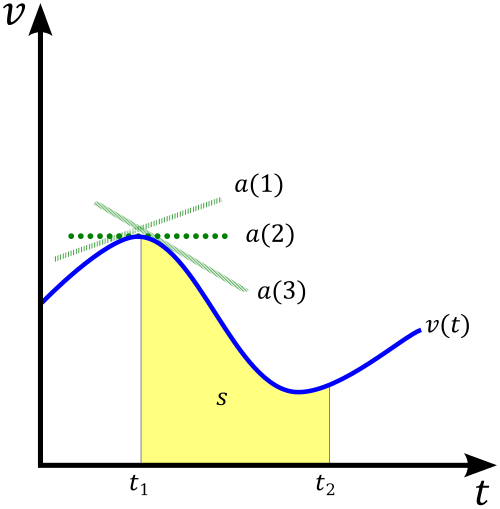
This diagram shows velocity as a function of time, with shaded regions under the curve representing signed areas corresponding to displacement. In calculus, these areas relate to the integral of velocity, while total distance uses to ensure nonnegative accumulation. The graphic also includes acceleration and displacement labels, which go slightly beyond the syllabus focus but remain conceptually aligned. Source.
In a calculus context, these areas correspond to displacement, while the total distance traveled is obtained by integrating the speed, , so that all contributions are nonnegative.
When Using a Table of Values for Velocity
Students may approximate the integral by:
Interpreting the table entries as rates.
Applying numerical estimation techniques where needed.
Taking absolute values before accumulating changes to ensure all contributions reflect the magnitude of velocity.
These skills ensure students can generalize the concept of total distance to varied data formats, consistent with AP expectations.
Conceptual Comparison: Distance vs. Displacement
Understanding the distinction between total distance and displacement strengthens comprehension. Although the AP syllabus highlights total distance through the integral of speed, connecting it to displacement improves conceptual accuracy.
Term: Displacement — The net change in position over a time interval, computed as the integral of velocity, which accounts for direction.
Displacement may be smaller than total distance because negative velocity offsets positive velocity.
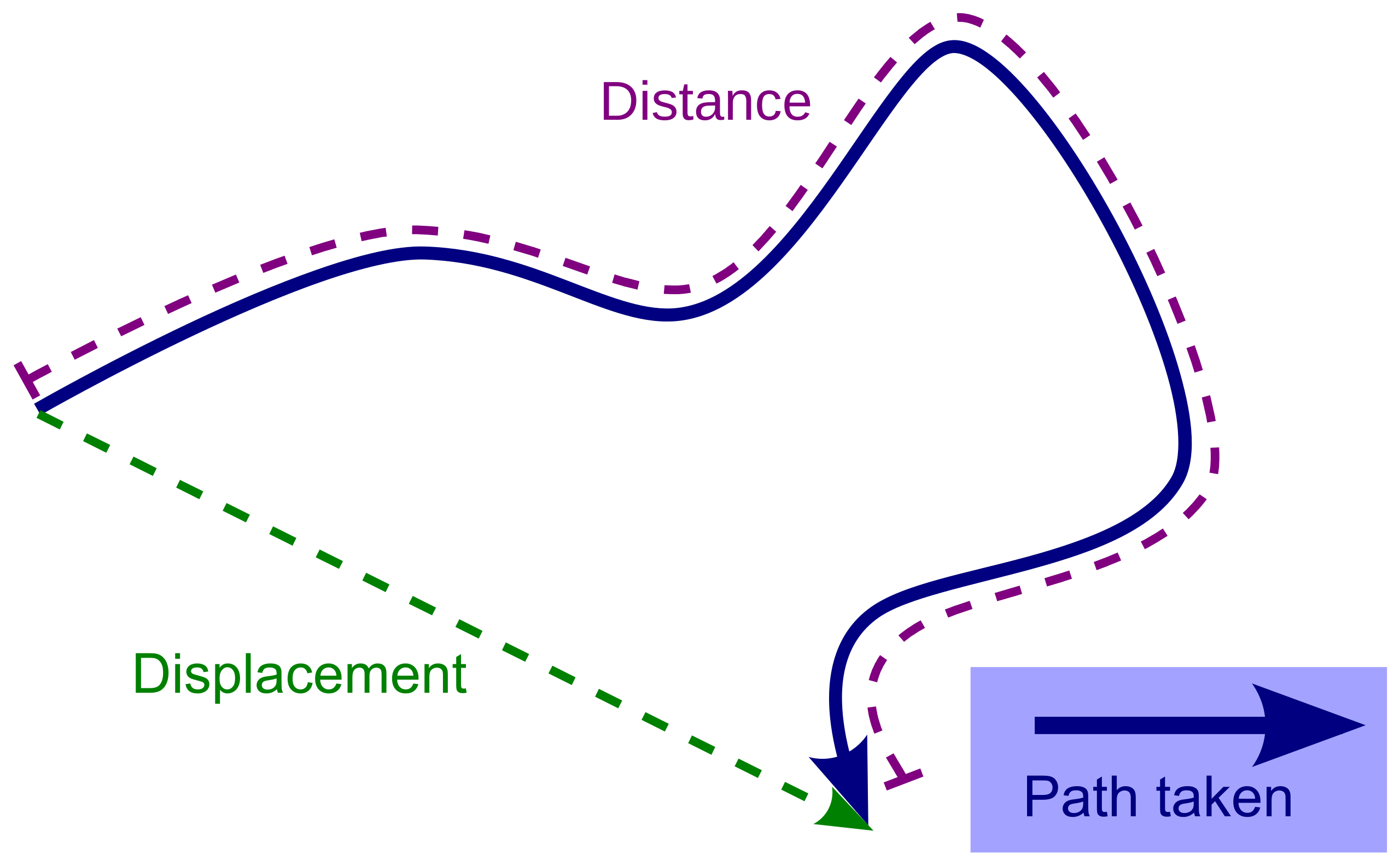
This diagram contrasts the total path length (distance) of an object following a curved route with the straight-line displacement vector between start and end points. It highlights that distance is the full path length while displacement measures only the net position change, consistent with using for total distance. The graphic is focused on the core comparison and does not introduce extraneous concepts. Source.
In contrast, total distance reflects the full length of the path traveled.
Interpreting Total Distance in Motion Contexts
Real-world motion frequently involves changes in direction—vehicles slowing and reversing, objects thrown into the air, or particles oscillating. In each case, total distance traveled involves the accumulation of all movement, and speed provides the correct integrand for this accumulation. The integral of speed captures how much ground is covered without regard to directional shifts, reinforcing the physical interpretation of distance as a nonnegative path length.
This interpretation aligns with the syllabus focus: the definite integral of speed gives the total distance traveled over a time interval, ensuring accurate accumulation even when velocity changes sign.
FAQ
Use the integral of speed whenever the problem asks for how far a particle actually travels along its path.
This typically appears in phrases such as:
• total distance
• length of the path
• how far the particle travels
If the question mentions net change in position, the integral of velocity should be used instead.
Distance must always be non-negative, but velocity can take negative values when the particle moves in the opposite direction.
Applying the absolute value converts all velocity values into positive speeds, making every segment of motion contribute positively to the accumulation.
This approach ensures that backwards movement does not cancel forwards movement.
Areas where the velocity has a large magnitude, regardless of sign, contribute significantly to total distance.
Look for:
• steep slopes leading to large vertical values
• wide intervals where velocity stays far from zero
• extended sections below the time axis, which will still count positively once the magnitude is taken
Large shaded areas (ignoring sign) mean larger total distance.
A turning point in position occurs when the particle switches direction, which happens exactly when velocity becomes zero.
Even if position is not explicitly provided, finding where v(t) = 0 reveals the critical times at which motion reverses.
These times divide the interval into segments where the sign of velocity is constant, allowing total distance to be computed accurately.
Yes. When given tables or rough data, numerical methods can approximate the integral of speed.
Common approaches include:
• the trapezium rule applied to absolute velocity values
• midpoint or left-endpoint sums if the data represent rate values at selected times
Always ensure each velocity value is replaced by its magnitude before applying the numerical method.
Practice Questions
A particle moves along a straight line with velocity v(t) given in metres per second for t between 0 and 4 seconds. Its velocity is positive on 0 ≤ t < 2 and negative on 2 ≤ t ≤ 4. The speeds at the endpoints are: v(0) = 3, v(2) = 0, and v(4) = −4. Explain why the total distance travelled on 0 ≤ t ≤ 4 cannot be found by integrating v(t) alone.
(1–3 marks available)
• 1 mark: States that integrating v(t) gives displacement rather than total distance.
• 1 mark: Explains that negative velocity values reduce the integral, cancelling part of the motion.
• 1 mark: States that total distance requires integrating the speed, the magnitude of velocity, ensuring all contributions are positive.
A particle moves along a line, and its velocity v(t) in metres per second is given by the graph of v(t) for 0 ≤ t ≤ 9. The graph is piecewise linear.
• From t = 0 to t = 3, the graph is a straight line rising from v = 0 to v = 6.
• From t = 3 to t = 5, the velocity decreases linearly to v = −2.
• From t = 5 to t = 9, the velocity increases linearly to v = 4.
(a) Determine the time(s) at which the particle changes direction.
(b) Compute the total distance travelled on 0 ≤ t ≤ 9.
(c) Explain the difference between displacement and total distance in the context of this motion.
(4–6 marks available)
(a) (1 mark)
• 1 mark: Identifies t = 3 and t = 5 as the direction-change times (velocity changes sign at t = 3→positive to negative and t = 5→negative to positive).
(b) (3–4 marks)
• 1 mark: Computes distance on 0 ≤ t ≤ 3 by finding the area of the triangle (base 3, height 6 → distance 9).
• 1 mark: Computes distance on 3 ≤ t ≤ 5 using the triangular area (base 2, height 2 → distance 2).
• 1 mark: Computes distance on 5 ≤ t ≤ 9 using the trapezium (or triangle) area (distance 14).
• 1 mark: Total distance stated as 25 units (accept equivalent numerical reasoning).
(c) (1 mark)
• 1 mark: States clearly that displacement is the net change in position (signed), whereas total distance is the sum of all movement regardless of direction.

