AP Syllabus focus:
‘Students interpret integrals of velocity and speed in motion contexts to find positions, displacement, and distance traveled, viewing definite integrals as accumulation of change in position.’
Interpreting integrals in motion problems requires understanding how velocity and speed describe change over time and how definite integrals accumulate this change to determine displacement and total distance traveled.
Understanding Integrals in Motion Contexts
Motion problems in AP Calculus AB rely on connecting a particle’s velocity function to its movement along a line. Because velocity represents the instantaneous rate of change of position, integrating it over a time interval provides an accumulated measure of how far and in what direction the particle travels. This subsubtopic focuses on interpreting these integrals rather than computing them, emphasizing conceptual meaning in terms of real motion.
Interpreting Velocity as a Rate of Change
Velocity describes how quickly and in which direction a particle moves. When the velocity function is integrated over a time interval, the definite integral represents a net positional change. Because velocity can be positive or negative, the accumulated value reflects direction as well as magnitude.
Displacement from Integrating Velocity
Displacement refers to a particle’s overall change in position on an interval, considering movement both forward and backward. In motion problems, students frequently interpret a definite integral of velocity as displacement rather than total distance.
= Velocity function (units: position per unit time)
= Start and end of the time interval
This relationship highlights that areas above and below the time axis represent forward and backward motion, respectively, and they combine algebraically. A positive integral indicates net forward progress, while a negative result implies overall backward movement.
Total Distance Traveled as Accumulated Speed
Unlike displacement, total distance traveled accumulates the entire path length regardless of direction. Thus, AP Calculus AB emphasizes interpreting the integral of speed, which is the absolute value of velocity. Total distance is always nonnegative and increases as the particle moves, whether in the positive or negative direction.
= Speed (units: nonnegative position per unit time)
= Bounds of the time interval
Because speed is always nonnegative, the integral measures pure accumulated travel without cancellation. Interpreting this requires understanding when velocity is positive or negative and how that affects the motion.
A clear conceptual difference exists between the two integrals: displacement accounts for net change, while total distance accounts for cumulative travel. Recognizing this distinction is essential when reading graphs or tables of velocity.
Using Graphs to Interpret Integrals of Velocity and Speed
Graphs of velocity versus time provide essential tools for understanding motion. Students must associate signed area with displacement and total nonnegative area with distance.
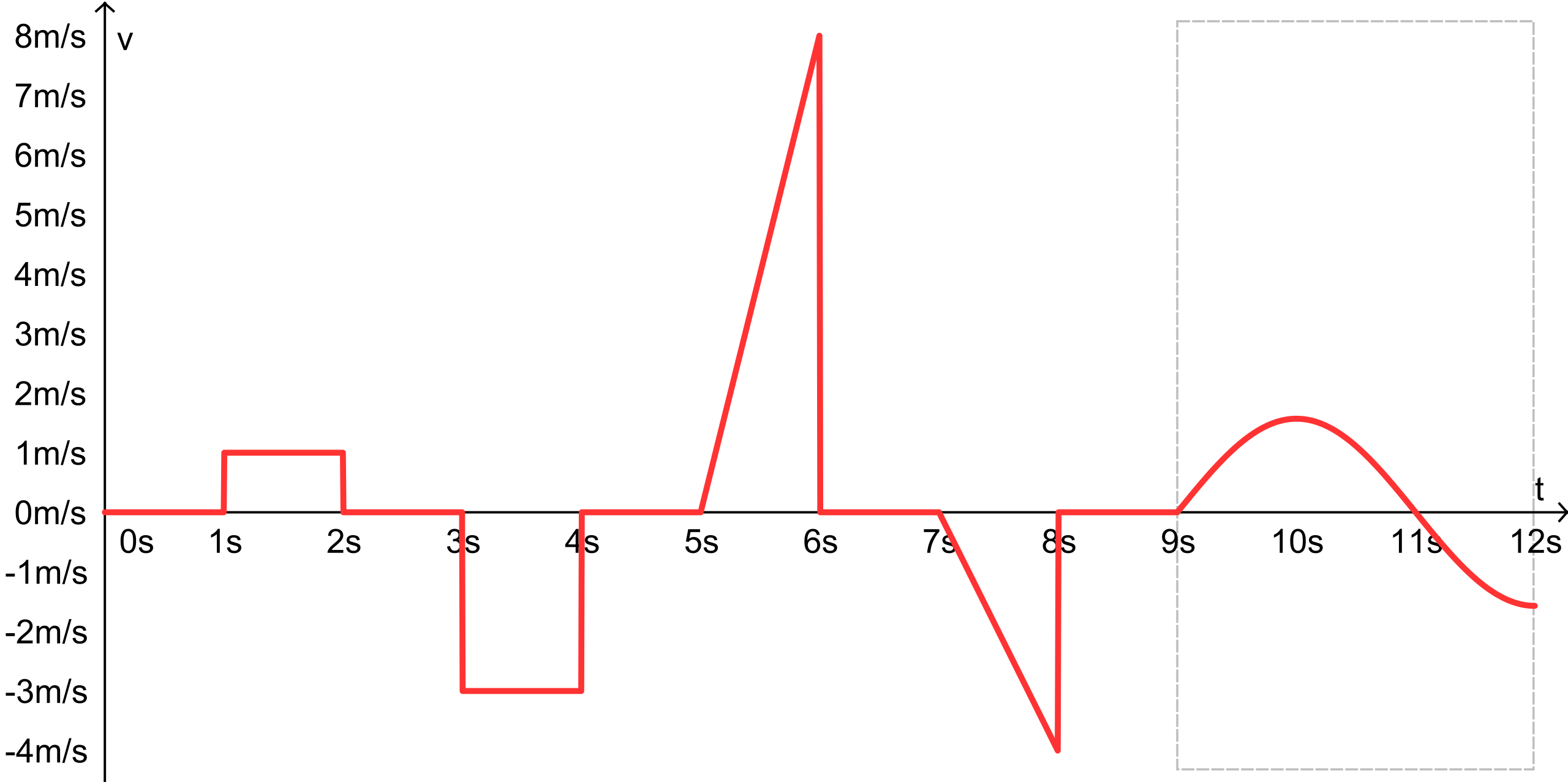
Velocity–time graphs illustrate how an object’s velocity changes over time for different motions. Each curve corresponds to a distinct pattern of motion, such as constant or changing velocity. The diagram includes additional comparative motion details that can be ignored while focusing on interpreting areas under the curves as integrals. Source.
This interpretation connects the geometric meaning of definite integrals to physical movement.
Key Interpretive Ideas from Velocity Graphs
When analyzing a velocity graph, students identify where the graph lies above or below the horizontal axis. These regions tell whether the particle moves forward or backward. The interpretation relies on the following principles:
Area above the axis corresponds to forward motion.
Area below the axis corresponds to backward motion.
Signed area (positive minus negative) gives displacement.
Total area (all positive) gives distance traveled.
These ideas allow students to evaluate or estimate integrals without explicit formulas, relying on visual reasoning or numerical approximations from graph features such as geometric shapes or plotted values.
Using Tables to Interpret Integrals of Velocity and Speed
In many AP problems, velocity values are supplied in tables rather than formulas. Students interpret integrals numerically through estimation techniques, recognizing that the integral still represents accumulated change.
Table-Based Interpretation Principles
When dealing with a table of velocity values over time, students rely on approximations to understand the meaning of the integrals:
Combine interval-by-interval contributions to approximate displacement.
Apply absolute value before accumulation when estimating total distance.
Recognize that increasing or decreasing velocity values indicate changes in motion behavior.
Ensure careful attention to sign when determining displacement from table entries.
Students must always relate these numerical processes back to conceptual meaning: total change in position and total distance traveled.
Motion Problems Requiring Conceptual Interpretation
Word problems involving motion require translating verbal descriptions into conclusions about displacement or distance. The definite integral plays the role of an accumulator of change, and interpreting it correctly means understanding what quantity is changing and how it changes over time.
Interpreting Verbal Descriptions of Motion
Students may encounter statements describing objects speeding up, reversing direction, or maintaining velocity over different intervals.
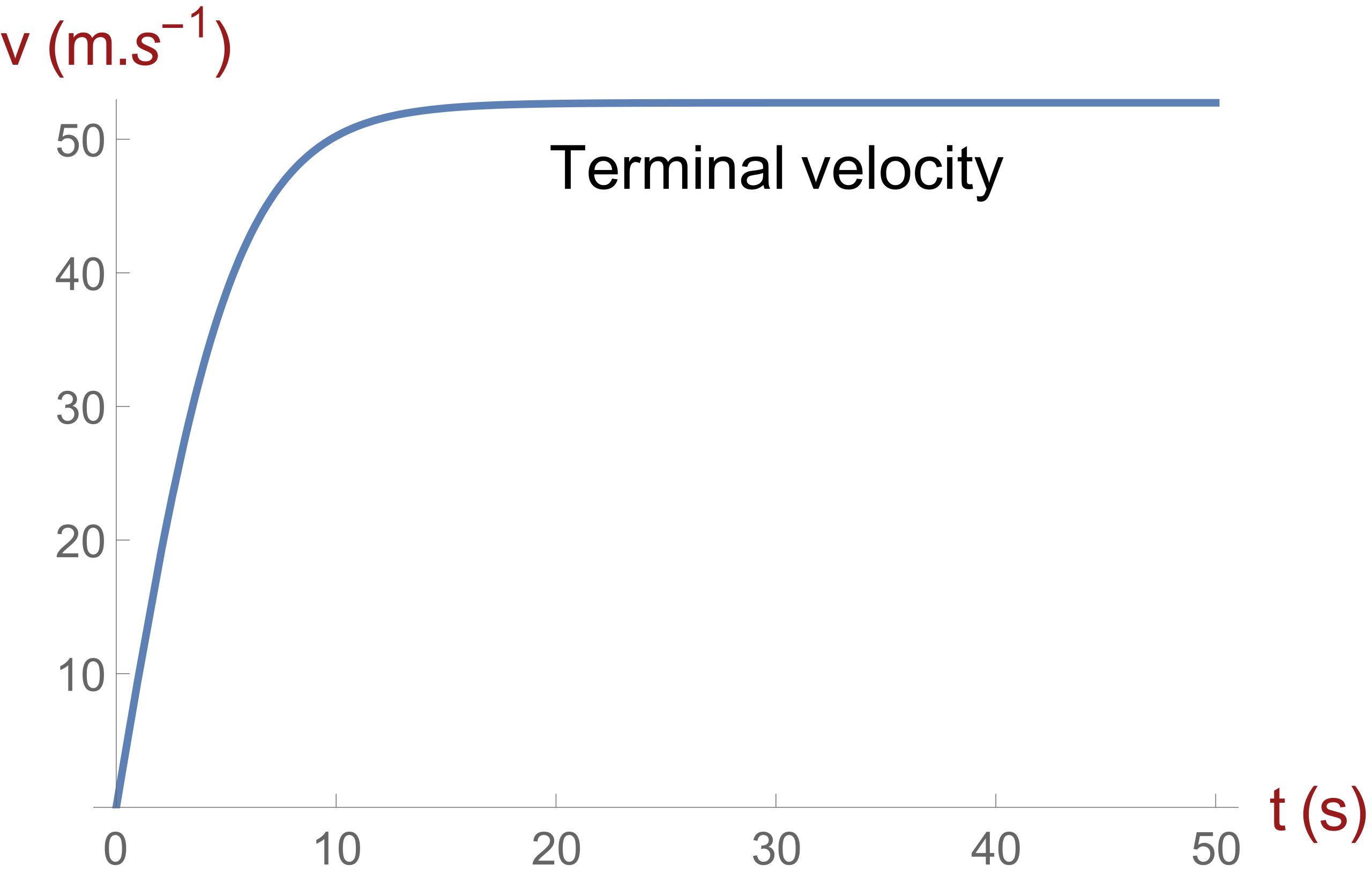
The graph shows a skydiver’s velocity increasing from near zero and approaching a constant terminal value as time passes. Interpreting the area under this curve as an integral of yields the skydiver’s displacement from the jump point. The precise parameter details on the source page exceed syllabus needs but do not affect interpreting the integral conceptually. Source.
In these scenarios, interpreting integrals involves identifying what the integral represents and why:
When the problem asks for change in position, interpret the integral of velocity as displacement.
When it asks for how far the object traveled, interpret the integral of speed as total distance.
When the direction changes, treat forward and backward contributions separately for displacement and take absolute values for distance.
When the problem references accumulated motion over time, rely on the fundamental idea that definite integrals represent accumulated change.
These interpretive skills enable students to analyze motion without needing explicit computations, aligning with the syllabus’s emphasis on conceptual understanding of integrals in motion contexts.
FAQ
A change in direction occurs when velocity changes sign. On a graph, this appears when the curve crosses the time axis.
You should examine the exact times where the curve touches or intersects the axis. These are turning points in the particle’s motion and separate portions of forward and backward travel.
Bullet-point check:
• Above the axis: moving forwards
• Below the axis: moving backwards
• Crossing the axis: direction change
A zero integral indicates that the total signed area above the axis exactly cancels with the signed area below it.
This means the particle’s net change in position is zero even though it may have travelled a non-zero distance. The particle ends the interval exactly where it started, but not necessarily by remaining still.
Accuracy depends on the size of the intervals and the method of estimation.
Smaller subintervals improve reliability. Using midpoint or trapezoidal approximations is typically more accurate than left or right endpoint methods.
Checklist:
• Smaller intervals → better estimates
• Midpoint/trapezoidal → usually more accurate
• Always interpret your estimate in the context of motion
Speed is always non-negative, so integrating it accumulates every bit of movement without cancelling.
Negative velocity represents backwards motion. If you integrated velocity directly, backwards portions would subtract from forwards portions. Using speed avoids this and ensures every segment contributes positively.
This is why total distance must be based on speed, not velocity.
When velocity is constant, both displacement and distance grow at a steady rate.
For such intervals, the area under the velocity curve forms a rectangle, making interpretation easier:
• Height = constant velocity
• Width = time duration
• Area = amount of movement
Even though the calculation is simpler, its meaning still depends on whether velocity is positive or negative.
Practice Questions
A particle moves along a straight line with velocity v(t) measured in metres per second. The graph of v(t) lies entirely above the time axis on the interval 0 ≤ t ≤ 4. Explain what the definite integral from 0 to 4 of v(t) dt represents in the context of the particle’s motion.
Question 1 (1–3 marks)
• 1 mark: States that the integral represents the total distance travelled or displacement.
• 1 mark: Identifies that because velocity is always positive, the value represents total distance rather than signed displacement.
• 1 mark: Provides correct context, e.g., “It gives the accumulated movement of the particle over the interval”.
Maximum: 3 marks.
A particle moves along a line with velocity v(t), measured in metres per second, for 0 ≤ t ≤ 10. The velocity is positive on 0 ≤ t < 3, negative on 3 ≤ t ≤ 7, and positive again on 7 < t ≤ 10.
(a) State what the definite integral from 0 to 10 of v(t) dt represents.
(b) Explain how you would determine the total distance travelled on the interval 0 ≤ t ≤ 10.
(c) Suppose the areas under the graph of v(t) above the axis on 0 ≤ t < 3 and 7 < t ≤ 10 are 12 metres and 9 metres respectively, and the area below the axis on 3 ≤ t ≤ 7 is 15 metres. Calculate the displacement and the total distance travelled.
Question 2 (4–6 marks)
(a)
• 1 mark: States that the integral represents the displacement of the particle from t = 0 to t = 10.
(b)
• 1 mark: States that total distance is found by integrating the speed, or equivalently by taking the integral of the absolute value of velocity.
• 1 mark: States that this requires adding areas above the axis and subtracting none for negative velocity (i.e., treat all contributions as positive).
(c)
• 1 mark: Calculates displacement as 12 − 15 + 9 = 6 metres.
• 1 mark: Calculates total distance as 12 + 15 + 9 = 36 metres.
Maximum: 6 marks.

