Understanding volume through accumulated area provides a unifying perspective on solids with known cross sections, showing how integration aggregates infinitesimally thin slices into a complete three-dimensional solid.

Viewing Volume as Accumulated Area

In many geometric and applied contexts, a solid can be described by analyzing how its cross-sectional area changes along an axis. A cross section is a two-dimensional slice of the solid, usually taken perpendicular to either the $x$-axis or the $y$-axis.

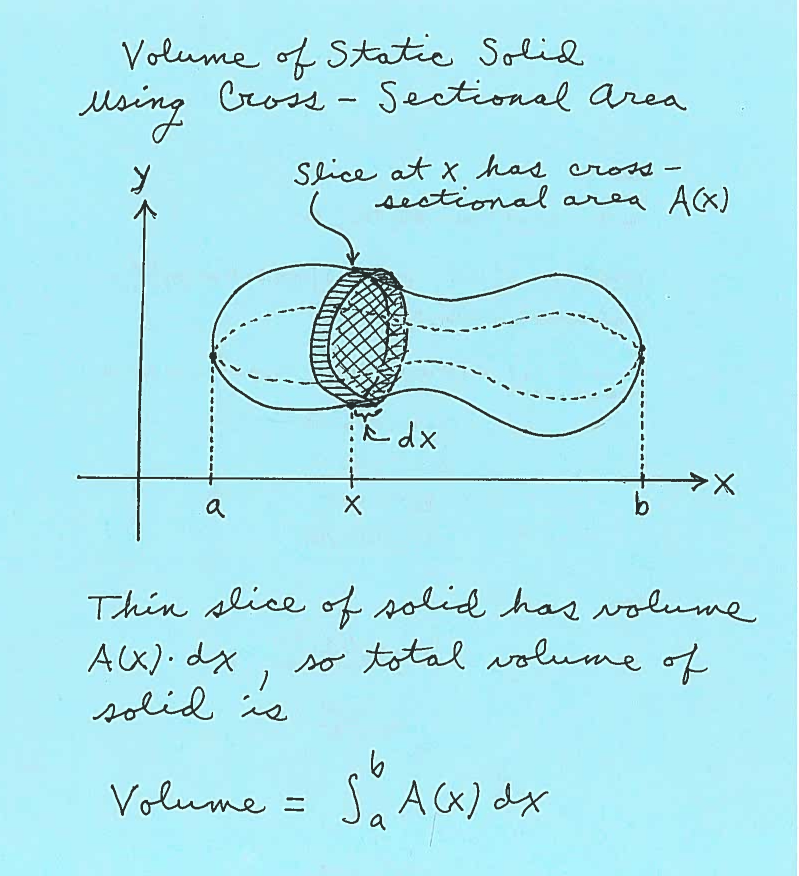
This diagram illustrates a solid above the $x$-axis with a typical slice at position $x$ having area $A(x)$ and infinitesimal thickness $dx$. Thinking of the volume as the sum of these tiny slices leads to the integral $V=\int_a^b A(x),dx$. The image reflects the AP idea that volume is an accumulation of cross-sectional areas along an interval. Source.

The central idea of this subsubtopic is that the volume of the solid is the accumulation of these areas, summed continuously through a definite integral.

When a cross-sectional area varies with position, we interpret volume as accumulated change in the same way integrals measure accumulated distance or accumulated net change. This connection reinforces the AP Calculus AB perspective that definite integrals express total quantities built from infinitesimal contributions.

The Role of the Area Function

If the area of a cross section at location $x$ is represented by a function $A(x)$, then the definite integral of $A(x)$ over an interval gives the volume of the solid.

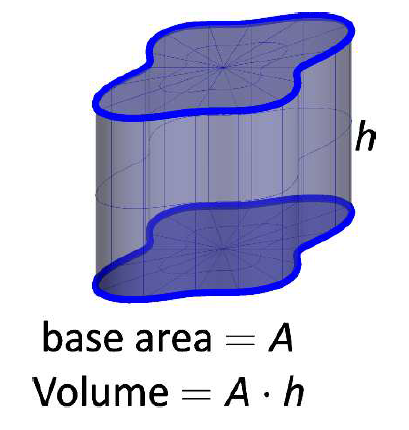
This figure shows a right cylinder whose volume is computed as area of the base times its height. It demonstrates the simplest case of viewing volume as cross-sectional area multiplied by thickness, which generalizes to the integral $V=\int_a^b A(x),dx$ when the area varies. The cylinder is a specific example, but the underlying accumulation idea applies to all solids with known cross sections. Source.

This representation emphasizes that every slice contributes a small amount of volume that builds toward the total.

This formulation relies on understanding that each slice is treated as having an infinitesimal thickness $dx$, enabling the integral to sum continuously across the domain. The definite integral becomes a natural mathematical expression of the idea that volume arises from stacking infinitely many very thin slices whose areas vary smoothly.

Interpreting Accumulation in Cross-Sectional Volume

The phrase accumulated area refers to the idea that each slice contributes only a small part of the total volume, but the integral aggregates these parts without missing any detail in the shape of the solid. This view is consistent with the AP requirement that students interpret integrals as measurements of accumulated change, here applied directly to geometric volume.

Because volume depends on area, and area depends on the geometry of the cross section, students must understand how the solid is generated. A base region in the plane typically defines the width or radius of each slice, and the known cross-sectional shape—such as a square, rectangle, triangle, or semicircle—determines the area formula. The area formula is then expressed in terms of $x$ or $y$, depending on orientation.

A normal sentence explaining the importance of orientation ensures the correct choice of variable when writing the integral.

Orientation and Choice of Variable

A solid may be defined so that its cross sections are perpendicular to either the $x$-axis or the $y$-axis. The variable of integration should match the direction of slice accumulation:

• Perpendicular to the $x$-axis: Cross sections are functions of $x$, and volume is expressed using $\int A(x), dx$.

• Perpendicular to the $y$-axis: Cross sections are functions of $y$, and volume is expressed using $\int A(y), dy$.

The choice of orientation depends on which axis allows the cross-sectional dimensions to be expressed more simply. AP Calculus AB students are expected to interpret the geometric description, determine which orientation provides a clearer area function, and then represent the accumulated volume with an appropriate definite integral.

Understanding the Base Region’s Role

The base region anchors the geometry of the solid. Although volume is determined by cross-sectional area, the base region identifies where slices begin and end, and provides the measurements needed to determine side lengths, radii, or widths used in the area function. The interplay between the base and cross sections reinforces that a three-dimensional solid can be analyzed systematically through two-dimensional components.

A base region might be a bounded region in the $xy$-plane, the interval between two curves, or the area between a function and an axis. The definite integral uses the limits that correspond to the edges of this region.

A normal sentence ensures clarity before the next structured content.

Conceptualizing the Solid as a Sum of Slices

Viewing volume as the accumulation of area helps students visualize how three-dimensional objects relate to functions and integrals. Because the cross-sectional approach generalizes across many shapes, it allows the same strategy to be applied to varied solids:

• Solids with constant cross sections

• Solids with increasing or decreasing cross sections

• Solids whose base shapes change geometry along the interval

• Solids where formulas involve radii, widths, or other dimensions derived from given functions

This approach also emphasizes that the definite integral is not merely a computational tool but a conceptual representation of accumulation. It connects closely to earlier ideas from the Fundamental Theorem of Calculus, where integrating a rate yields a total accumulated quantity.

Linking Cross Sections to Accumulated Volume

To represent volume effectively:

• Identify the axis perpendicular to the cross sections.

• Describe the geometry of each slice using the base region.

• Find the area formula for the cross section in terms of the chosen variable.

• Write a definite integral that accumulates this area across the interval.

This perspective aligns directly with the AP specification, which highlights that volumes with known cross sections are understood as the accumulation of cross-sectional areas, using definite integrals to sum slices and fully determine the solid’s volume.