Solids of revolution around the coordinate axes arise when a planar region is rotated about either the x-axis or y-axis, creating a three-dimensional solid whose volume is determined using definite integrals.

Understanding Solids of Revolution

A solid of revolution is generated when a two-dimensional region in the coordinate plane is rotated about a fixed axis. This rotation forms a three-dimensional object whose cross sections perpendicular to the axis of rotation are circles. Because these circular cross sections represent accumulated slices of volume, definite integrals provide the natural mathematical tool for determining total volume.

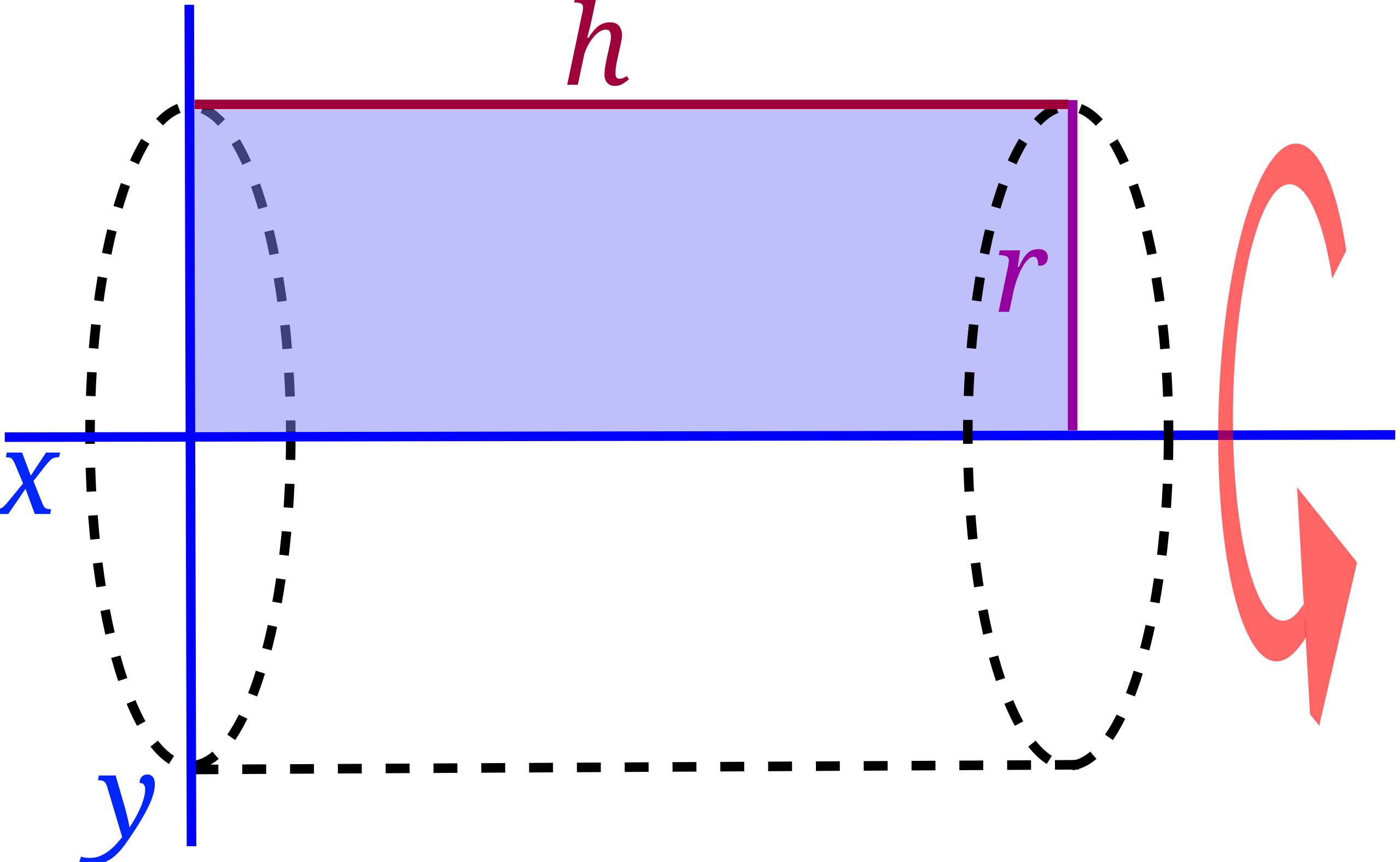
This diagram shows a rectangle of height $r$ and length $h$ being rotated about the $x$-axis to form a right circular cylinder. The red arrow indicates the axis and direction of rotation, and the shaded rectangle represents the generating region in the plane. This connects the geometric formula $V=\pi r^2 h$ to the idea of a solid of revolution formed from a planar region. Source.

The Role of Cross-Sectional Geometry

When a region is revolved around a coordinate axis, each perpendicular slice of the resulting solid becomes a disc, a circular slice whose radius depends on the distance from the curve to the axis. Before introducing formulas, it is helpful to understand what radius represents in this context. The radius at a particular point reflects how far the original graph lies from the chosen axis of revolution, making the radius a function of the independent variable.

The radius changes as the function changes, meaning that accumulating discs with varying radii naturally requires integration.

A solid of revolution around the x-axis uses horizontal slicing, while rotation around the y-axis uses vertical slicing. The orientation must match the variable of integration to ensure that each cross section is perpendicular to the axis.

Generating Solids Around the x-Axis

Revolving a region around the x-axis creates discs stacked along the x-direction. The radius of each disc is determined by the vertical distance from the curve to the x-axis. If the function defining the boundary is $y = f(x)$, then the radius is simply $f(x)$. The method depends on interpreting the solid as an accumulation of circular slices, each contributing an incremental volume amount.

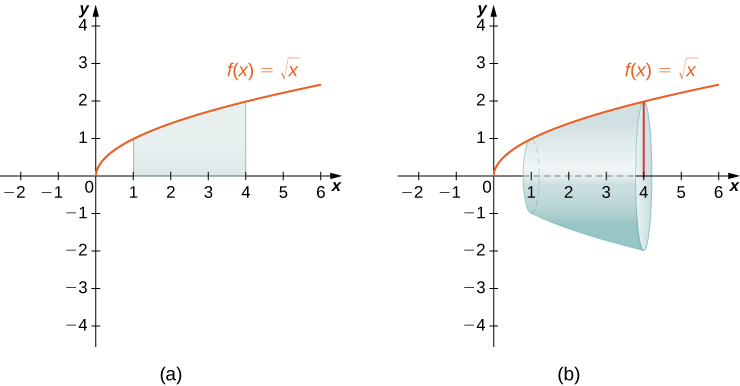
The left panel shows the region under $f(x)=\sqrt{x}$ above the $x$-axis on $[1,4]$, which serves as the generating region. The right panel shows the solid obtained when this region is revolved about the $x$-axis, forming a shape whose cross sections perpendicular to the axis are circular discs. This visually supports the disc method formula $V=\int_a^b \pi [f(x)]^2,dx$ without adding concepts beyond the AP syllabus. Source.

Disc Volume Through Integration

To determine the volume of the entire solid, the area of a representative disc is integrated across the interval where the solid is formed.

The definite integral accumulates infinitely many disc areas, reflecting how rotation creates continuous three-dimensional volume from a continuous function.

Because discs are circular, using $\pi r^2$ naturally incorporates the geometry of revolution. The process emphasizes interpreting volume as accumulated area, which aligns with the fundamental interpretation of definite integrals as total accumulated change.

Generating Solids Around the y-Axis

When revolving a region around the y-axis, the process is analogous, but the radius must be expressed using horizontal distance. In this case, the function is written in terms of $x$ as a function of $y$, or the curve must be invertible so that the horizontal distance to the axis can be measured correctly.

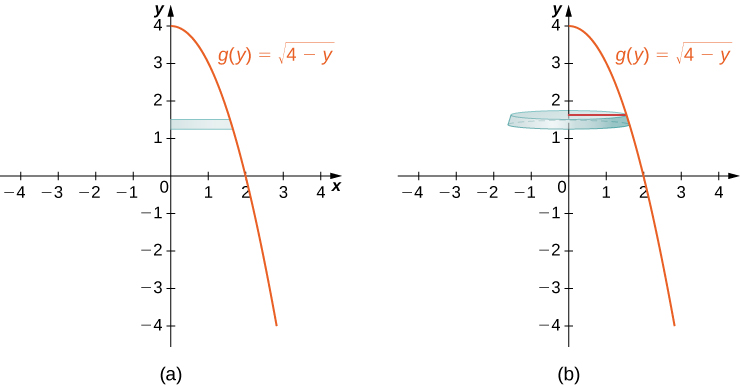
The left panel shows a thin horizontal rectangle between the curve $g(y)=\sqrt{4-y}$ and the $y$-axis, representing a slice whose length is the disc radius. The right panel shows the corresponding horizontal disc produced by rotation about the $y$-axis. The diagram emphasizes that for rotation around the $y$-axis, the radius is a function of $y$ and volume is computed with $V=\int_c^d \pi [g(y)]^2,dy$. Source.

Understanding the Radius in y-Axis Rotation

Because each disc is perpendicular to the y-axis, its radius corresponds to the x-value of the bounding function. If the boundary is given as $x = g(y)$, then the radius is $g(y)$, and integration proceeds with respect to $y$. The orientation must always match the axis of revolution so that each slice remains circular.

This formulation highlights that solids of revolution depend more on geometric orientation than on the specific algebraic form of the function. Identifying whether the radius is vertical or horizontal is essential for correctly setting up disc integrals.

A normal sentence must appear between boxed elements to satisfy formatting guidelines. In many problems, functions may need to be rewritten or interpreted graphically to express the radius appropriately.

Visualizing Accumulated Circular Slices

The concept of accumulated circular discs is foundational to understanding this subsubtopic. Each disc contributes a small volume slice, and the definite integral sums these contributions. The disc method appears whenever a region is revolved around a principal coordinate axis without creating a hollow center. Because the slices are solid discs rather than rings, no inner radius exists.

Key Features of Disc-Based Solids of Revolution

The following points summarize essential characteristics of solids formed using this method:

• The cross sections perpendicular to the axis of rotation must be solid discs, not washers.

• The radius is always measured directly from the generating curve to the axis of rotation.

• The integral bounds correspond exactly to the interval defining the base region.

• The integrand represents the area of each disc, which is always $\pi (\text{radius})^2$.

• The method applies cleanly only when the entire region touches the axis of revolution without forming an inner cavity.

Importance in the AP Calculus AB Curriculum

This subsubtopic establishes the conceptual foundation for later work with washers and shells. Understanding rotation around the x- or y-axis is crucial because it introduces the geometric structure used throughout applications of integration. The emphasis on interpreting volume as an accumulation of area strengthens students’ conceptual understanding of definite integrals and reinforces the idea that integration unifies many geometric and physical problems by capturing continuous change.