A strong or weak correlation can easily be misinterpreted, so understanding its limitations is essential for avoiding incorrect conclusions about relationships in quantitative data.

Misinterpretations of Correlation

Understanding Why Correlation Can Be Misleading

The correlation coefficient, introduced here as correlation (r), measures the direction and strength of a linear association between two quantitative variables. Students often assume that a large positive or negative value of r guarantees a meaningful linear model, but the specification emphasizes that this assumption can be incorrect. A high magnitude of r does not ensure that the relationship is linear, meaningful, or suitable for prediction.

Because correlation reflects only linear relationships, it can disguise nonlinear patterns or structural irregularities in the data. Even datasets with identical values of r can have extremely different shapes, distributions, and suitability for linear modeling.

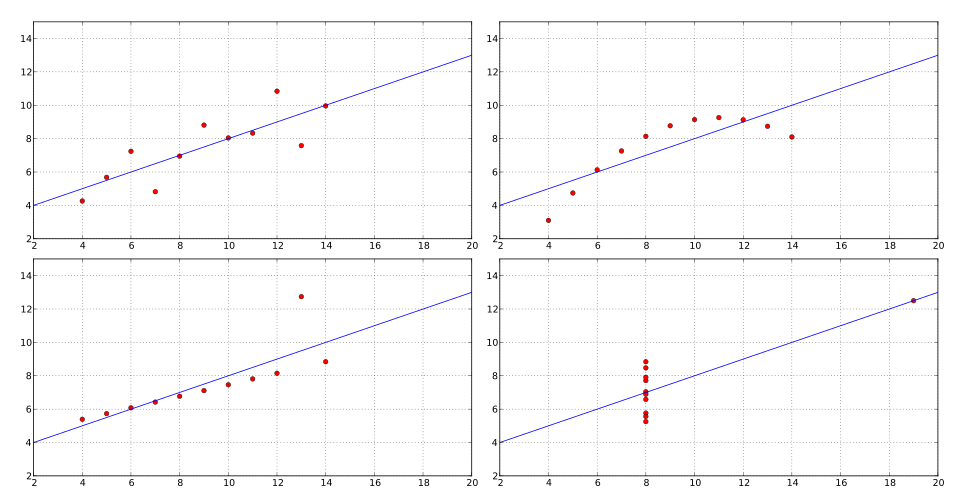
Anscombe’s quartet displays four datasets with nearly identical summary statistics—including correlation and regression lines—yet with very different shapes and patterns. This demonstrates that the same correlation value can describe relationships that differ fundamentally in form and linear suitability. It emphasizes the need to visualize data rather than rely on correlation alone. Source.

When Correlation Creates False Confidence

A common misunderstanding arises when students interpret a correlation value near 1 or –1 as evidence that two variables follow a linear pattern. The syllabus specifically warns that “a correlation coefficient close to 1 or -1 does not necessarily mean that a linear model is appropriate.” This highlights the need to inspect the full context and structure of the data rather than relying on r alone.

Key reasons correlation may be misleading include:

• Nonlinear relationships: Variables may have a strong association that is curved rather than linear.

• Clusters within data: Multiple subgroups can inflate or obscure correlation strength.

• Outliers: A single outlier can dramatically increase or decrease the value of r without representing the general pattern.

• Restricted ranges: Limiting the data to a narrow set of values can alter or distort the measured correlation.

These scenarios illustrate the limitations of correlation as a sole diagnostic tool.

Importance of Visualizing the Data

The specification underscores the necessity of visualizing data, particularly through scatterplots, before deciding whether a linear model is appropriate. A scatterplot allows students to examine form, direction, and strength while also observing any unusual features that correlation alone cannot capture.

Visualization helps reveal:

• Whether the relationship appears linear, curved, or random

• Whether certain groups of points follow different trends

• Whether influential or extreme points are present

• Whether a straight line would reasonably reflect the overall pattern

Because correlation cannot communicate any of these essential features, visual inspection becomes a critical step in preventing misinterpretation.

Outliers and Their Distorting Effects

One important source of misinterpretation involves outliers, which can disproportionately influence linear correlation. When an extreme data point lies far from the cluster of other observations, correlation may be artificially strengthened or weakened.

After recognizing this definition, it becomes clear that relying solely on r in the presence of outliers could lead students to draw conclusions that do not reflect the true structure of the data.

Since correlation assesses only the strength of a linear trend, it ignores curvature and other non-linear patterns.

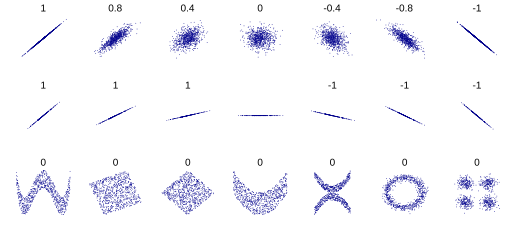
This figure shows scatterplots with similar or identical correlation coefficients but different slopes, shapes, and noise levels. Some panels include nonlinear structures, illustrating how correlation alone cannot describe curved relationships. These variations reinforce that correlation reflects only linear association, not overall form. Source.

Correlation and the Shape of the Association

Since correlation assesses only the strength of a linear trend, it ignores curvature and other non-linear patterns. A dataset might show an impressive absolute value of r, yet the scatterplot might reveal a shape that bends, curves, or changes direction. In these cases a linear model becomes inappropriate despite a seemingly strong numerical summary.

Students should carefully evaluate:

• The form of the relationship

• Whether a straight line fits the pattern

• Whether a transformation or nonlinear model might be more appropriate

• Whether the data are too variable to support any simple model

Understanding these points prevents overreliance on correlation values.

Correlation Does Not Confirm the Suitability of a Linear Model

The specification stresses that a strong correlation coefficient cannot validate a linear model on its own. Even when r suggests a strong linear association, a proper assessment requires:

• Reviewing the scatterplot

• Identifying any patterns inconsistent with linearity

• Considering variations or deviations across the range of x

• Examining whether certain segments of the data behave differently

Visual checks make it possible to determine whether the apparent strength measured by r reflects a genuine linear trend or if it is distorted by underlying structures.

Avoiding Overgeneralized Interpretations of Correlation

Students must avoid what is perhaps the most widespread misconception: the belief that correlation alone can determine model appropriateness or causality. While correlation quantifies the direction and strength of linear association, it does not describe form, account for outliers, or demonstrate causation. A high value of r provides only one piece of the analytical puzzle and must be interpreted with caution and context.

Practices for Responsible Interpretation

To apply correlation responsibly, students should:

• Always pair correlation values with graphical analysis

• Examine the full distribution of data points rather than summary values alone

• Remain cautious of extreme observations, clusters, and nonlinear shapes

• Confirm that a linear model aligns with the observed structure of the data

• Remember that strong correlation does not imply causation or appropriateness of prediction

These practices align directly with the syllabus emphasis on understanding the limitations of correlation and the importance of visual inspection before selecting a linear model.