This section introduces how the y-intercept functions within a least-squares regression model, focusing on interpretation, contextual meaning, and situations where it becomes misleading or inappropriate.

Understanding the Y-Intercept in Least-Squares Regression

The y-intercept occupies a central role in the structure of a simple linear regression model, which is expressed through the prediction equation $\hat{y} = a + bx$. In this context, the y-intercept, denoted by a, represents the predicted value of the response variable when the explanatory variable equals zero. Because of this, interpreting the y-intercept requires both mathematical understanding and careful consideration of context.

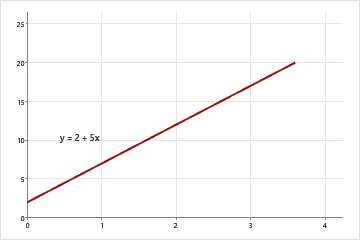
This graph illustrates a regression line with a positive slope and a y-intercept at 2, demonstrating how the intercept represents the predicted value when the explanatory variable is zero. The labeled slope shows how predictions rise with increasing x-values. The explicit slope label provides additional context beyond the subsubtopic’s focus on the y-intercept. Source.

In many real-world scenarios, the value of zero for the explanatory variable either makes sense or is theoretically meaningful. In other situations, however, zero lies far outside the observed data range or represents a condition that is impossible or illogical. As a result, the y-intercept must always be interpreted with careful reference to context to ensure that predictions or explanations are reasonable.

The Role of the Y-Intercept in the Regression Equation

The regression equation uses the y-intercept as a starting point for prediction, anchoring the line vertically on the coordinate plane. The slope then dictates how predictions change as the explanatory variable increases by one unit. When statisticians construct a least-squares regression line, the resulting y-intercept ensures that the line passes through the point representing the means of both variables, $(\bar{x}, \bar{y})$. This anchoring gives the model a specific balance that minimizes the squared residuals across all observations.

A regression model therefore integrates the y-intercept not merely as a mathematical artifact but as a component contributing to the model’s overall fit and predictive accuracy.

Interpreting the Y-Intercept in Context

Interpreting the y-intercept always requires asking whether a zero value for the explanatory variable is meaningful. When zero is realistic and lies within or near the range of the observed data, the y-intercept can provide valuable insight into baseline levels or starting values. In such cases, predictions at $x = 0$ align naturally with the structure of the regression model and support sensible conclusions about the relationship between variables.

However, when zero is far outside the observed data range, or when it represents a situation that does not or cannot occur, the applicability of the y-intercept becomes limited. The specification emphasizes that the y-intercept may “not have a logical interpretation within the context of the data,” meaning that predictions made at this value could be misleading or scientifically meaningless.

This scatterplot shows a regression line whose y-intercept is slightly below zero, illustrating a context where the predicted value at x = 0 has no logical meaning. The negative intercept contrasts with a response variable that cannot realistically take negative values. This reinforces the importance of evaluating whether zero is a meaningful or feasible value for the explanatory variable before interpreting the y-intercept. Source.

Why the Y-Intercept Sometimes Lacks Logical Interpretation

There are several reasons why the y-intercept may not be meaningful in a regression setting:

• Zero is outside the domain of the explanatory variable.
  When data only occur at positive values, predictions at zero reflect extrapolation beyond observed conditions.

• Zero represents an impossible or undefined state.
  Some measurements—such as age of college students or height of trees—cannot logically be zero, rendering the y-intercept irrelevant.

• The relationship itself is not linear near zero.
  Even when zero is technically possible, the trend may differ outside the observed data range.

When these conditions arise, the y-intercept still exists mathematically but should not be interpreted as a meaningful real-world prediction.

Using the Y-Intercept for Prediction

Although the y-intercept may not always be interpretable, it still affects predictions across the regression line. Its position determines the vertical placement of the line, ensuring that predictions at all relevant values of the explanatory variable align closely with observed patterns. Students should understand that a regression model remains valid even when the y-intercept itself cannot be given contextual meaning.

The y-intercept is therefore significant not because of its inherent interpretability but because of its role in shaping the model used to generate predictions across the data’s meaningful range.

Key Considerations for AP Statistics Students

When deciding how to interpret the y-intercept in a regression setting, students should rely on a structured evaluation process:

• Assess whether zero is a meaningful value for the explanatory variable.

• Determine whether zero falls within or near the observed data range, since large extrapolations weaken the prediction’s reliability.

• Evaluate the context to identify whether predictions at zero correspond to feasible or realistic conditions.

• Avoid assigning meaning when the value does not logically apply to the situation or contradicts common sense.

• Focus on the y-intercept’s role in forming the regression line, even when its real-world interpretation is absent.

The y-intercept thus illustrates a broader principle in statistics: mathematical quantities do not always translate directly into meaningful contextual interpretations. Understanding when and why this occurs is an essential analytical skill for interpreting least-squares regression models in applied settings.