AP Syllabus focus:
‘Delve into the characteristics of non-mutually exclusive events, contrasting with mutually exclusive events. Discuss how the occurrence of one event does not preclude the occurrence of the other, and how this concept influences the approach to calculating probabilities for such events, emphasizing the importance of understanding the distinction for accurately determining probabilities in various contexts.’
Non-mutually exclusive events appear frequently in real-world probability contexts, requiring careful interpretation because their outcomes can overlap and occur simultaneously.
Understanding Non-Mutually Exclusive Events
Non-mutually exclusive events represent situations in which two events can occur at the same time, meaning they share at least one outcome in common. This stands in contrast to mutually exclusive events, which have no overlapping outcomes and therefore cannot occur simultaneously. Because overlap is possible for non-mutually exclusive events, their probabilities must be calculated with attention to avoiding double-counting shared outcomes.
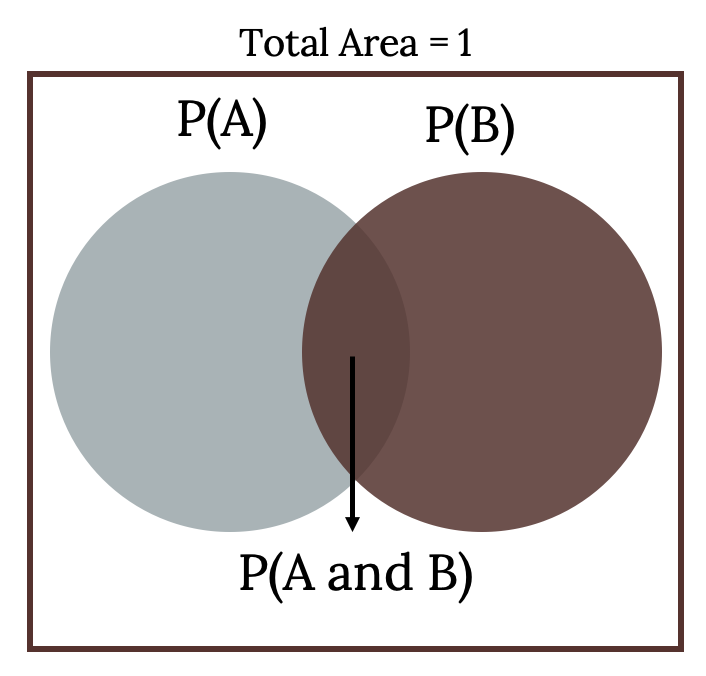
A Venn diagram illustrating how two non-mutually exclusive events overlap, with the intersection representing the probability of both events occurring. The rectangle outlines the full sample space, emphasizing that all probabilities must sum to 1. Labels extend slightly beyond syllabus requirements but clearly demonstrate how event areas relate within the sample space. Source.
When discussing this topic, it is essential to understand the term event, introduced here as a foundational concept.
Event: A collection of outcomes from a random process that satisfies a specific condition.
Non-mutually exclusive events play a central role in many probability applications, from card draws to survey responses, because real-world scenarios often involve categories that intersect rather than remain distinct. Recognizing whether events overlap is a critical first step in choosing the correct probability rule.
Identifying When Events Are Not Mutually Exclusive
Two events are not mutually exclusive when their occurrence is not restricted by the occurrence of the other. In other words, both events can occur in a single trial of the random process.
Key characteristics include:
Shared outcomes: Events possess at least one outcome that belongs to both sets.
Possibility of simultaneous occurrence: The occurrence of one event does not eliminate the possibility of the other occurring.
Need for adjusted probability calculations: Because overlap exists, probability rules must account for intersections.
To contrast: mutually exclusive events have P(A ∩ B) = 0. For non-mutually exclusive events, however, P(A ∩ B) > 0, meaning the intersection has probability greater than zero. This is the defining feature that shapes how probabilities are computed for such events.
The Relationship Between Events, Intersections, and Overlap
The intersection of two events is the set of outcomes that both events share.
Intersection (A ∩ B): The set of all outcomes that are common to both event A and event B.
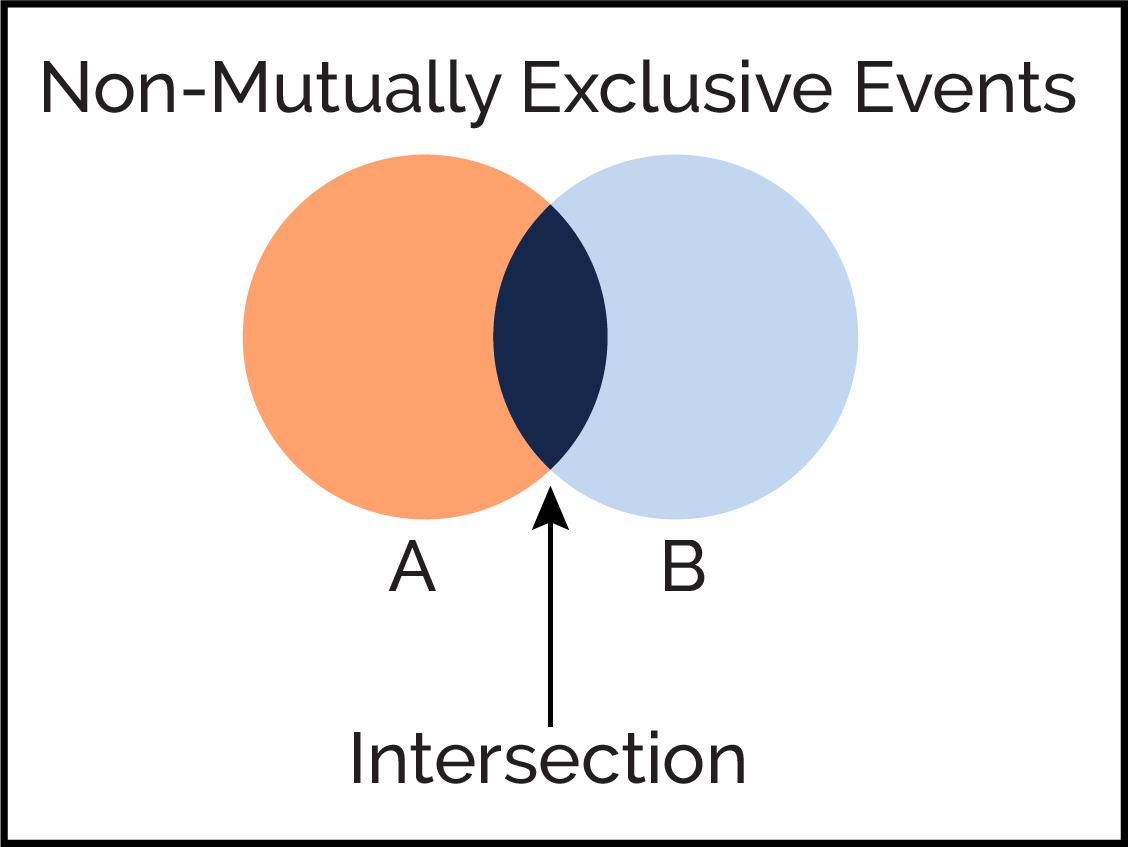
A diagram showing two overlapping events, A and B, with the shared region highlighted as the intersection. The labeled arrow emphasizes that these outcomes belong simultaneously to both events. This visual directly aligns with the concept that non-mutually exclusive events share outcomes rather than remain entirely separate. Source.
In the context of non-mutually exclusive events, the intersection is the crucial component that distinguishes these events from mutually exclusive ones. The presence of overlap impacts how we add probabilities for event unions.
Before presenting the addition rule, it is useful to highlight that intersections prevent simple summation of probabilities. If one were to simply add P(A) and P(B) for non-mutually exclusive events, the shared outcomes would be counted twice. This is why a correction term is needed.
The Addition Rule for Non-Mutually Exclusive Events
For non-mutually exclusive events, the probability that A or B occurs requires use of the general addition rule, which accounts for overlap.
EQUATION
= Probability that event A or event B (or both) occurs
= Probability of event A
= Probability of event B
= Probability that both events occur simultaneously
This rule is central to understanding non-mutually exclusive events because it ensures accurate probability calculation.
Why Recognizing Non-Mutually Exclusive Events Matters
Understanding non-mutually exclusive events is important for several reasons:
Accurate probability computations rely on identifying whether events overlap.
Statistical reasoning improves when students can distinguish between exclusive and non-exclusive structures.
Real-world applications commonly involve intersecting categories, making this concept broadly applicable.
Interpretation of data patterns often requires recognizing when outcomes belong to multiple groups simultaneously.
Non-mutually exclusive events support a broader understanding of probability’s role in analyzing uncertainty. Students must be able to determine whether events share outcomes and apply the correct rules accordingly. When this distinction is clearly understood, probability models become more precise and aligned with the structure of real-life scenarios.
FAQ
A useful first step is to check whether the events describe characteristics or behaviours that can realistically occur at the same time. If the categories overlap naturally, they are likely non-mutually exclusive.
You can also consider whether the events describe independent choices or traits, as these frequently overlap.
Observational data, such as survey responses with multiple selections allowed, often hints at non-mutual exclusivity.
Double-counting occurs because the same outcomes fall into both event sets, so adding P(A) and P(B) automatically counts the intersection twice.
This matters most when events share substantial overlap, as ignoring this can produce probabilities greater than 1 or misleading interpretations.
Subtracting the intersection corrects the duplication and preserves the logical structure of the sample space.
Scenarios with overlapping categories commonly generate non-mutually exclusive events, such as:
• Individuals reporting multiple preferences
• Situations where a single action fulfils more than one category
• Classifications based on broad traits rather than strict categories
These situations often arise in marketing surveys, social science research, and behavioural studies.
Students may assume events are mutually exclusive simply because they appear different on the surface, without considering whether they can occur together.
Another misconception is thinking that overlap requires a large number of shared outcomes; in fact, even a single shared outcome means the events are not mutually exclusive.
Students may also confuse the addition rule with that used for disjoint events, forgetting to subtract the intersection.
Correctly identifying overlapping events ensures that probability calculations reflect the structure of real-world situations rather than imposing artificial separation.
It prevents inflated probability totals and helps produce more reliable estimates for unions of events.
Accurate modelling supports better decision-making in fields such as risk assessment, resource planning, and consumer analysis, where overlapping characteristics are common.
Practice Questions
Question 1 (1–3 marks)
A group of 150 customers were surveyed about their preferences for two products: Product A and Product B.
Eighty customers liked Product A, 70 liked Product B, and 25 liked both.
Are liking Product A and liking Product B mutually exclusive events? Explain your answer.
Question 1 Mark Scheme
• 1 mark: States that the events are not mutually exclusive.
• 1 mark: Notes that mutually exclusive events cannot occur together.
• 1 mark: Justifies the answer using the fact that 25 customers liked both products, showing that the events overlap.
Question 2 (4–6 marks)
A university is analysing participation in two optional academic support programmes: Programme X (writing support) and Programme Y (study skills). Students may enrol in either programme, both, or neither.
The university has recorded the following probabilities:
P(X) = 0.52
P(Y) = 0.28
P(X and Y) = 0.14
(a) Explain why the events X and Y are not mutually exclusive.
(b) Calculate the probability that a randomly selected student participates in at least one of the programmes.
(c) Interpret your result from part (b) in the context of the university’s programmes.
Question 2 Mark Scheme
• Part (a) – 1–2 marks
1 mark: States that X and Y are not mutually exclusive.
1 mark: Explains that mutually exclusive events cannot occur together, but here P(X and Y) is greater than zero.
• Part (b) – 1–2 marks
1 mark: Uses or states the addition rule for non-mutually exclusive events (P(X) + P(Y) − P(X and Y)).
1 mark: Correctly calculates the probability: 0.52 + 0.28 − 0.14 = 0.66.
• Part (c) – 1–2 marks
1 mark: Interprets the probability as the likelihood that a student participates in at least one support programme.
1 mark: Provides a contextual statement (e.g., “About 66% of students use writing support, study skills, or both”).

