Interpreting probability distributions helps reveal meaningful characteristics of populations by examining how values are arranged, how often they occur, and what patterns emerge from their variability.

Understanding the Purpose of Interpretation

Interpreting a probability distribution involves analyzing how the possible outcomes of a random variable are spread out and how likely each value is. This interpretation allows statisticians to infer characteristics of a broader population from the distribution's structure. When students interpret a distribution, they focus on three essential features: shape, center, and spread, each offering different insights into the underlying random behavior.

Identifying the Shape of a Probability Distribution

The shape of a probability distribution refers to the general form created by plotting its values and associated probabilities. Interpreting shape helps determine whether data values cluster in certain regions or stretch across a range of possible outcomes. Key shape-related information can indicate the nature of the processes generating the data.

Common descriptive characteristics of distribution shape include:

• Symmetry: A symmetric distribution has identical behavior on both sides of its center.

• Skewness:

  • Right-skewed distributions have most probability mass on lower values with a long tail toward higher values.

  • Left-skewed distributions have most probability mass on higher values with a tail toward smaller values.

• Modality:

  • Unimodal distributions have one clear peak.

  • Bimodal or multimodal distributions have multiple peaks, suggesting varied underlying processes.

Understanding shape is critical because it influences how the center and spread should be interpreted and informs what conclusions are reasonable about the population represented by the distribution.

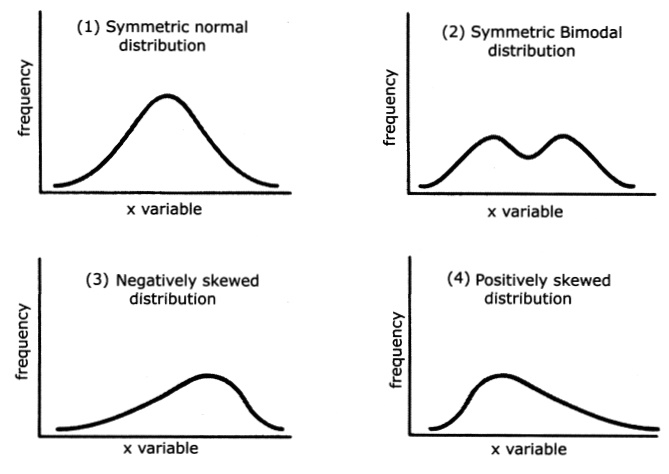
This image illustrates symmetric, bimodal, negatively skewed, and positively skewed distributions, highlighting how the concentration of probability and tail behavior determine a distribution’s shape. Although drawn using continuous examples, the same interpretive principles apply to probability distributions more broadly. Source.

Determining the Center of a Probability Distribution

The center describes the typical or expected value of the random variable. For discrete random variables, this idea is closely linked to the mean, which summarizes where the distribution tends to cluster.

Interpreting the center helps describe what value the random variable would approach over a very large number of repeated observations. The center provides a reference point from which other characteristics, such as spread, can be understood. It anchors the interpretation of the distribution in terms of what is typical for the population.

Between the center and the shape, students gain a clearer perspective on how the distribution behaves overall.

Examining the Spread of a Probability Distribution

The spread of a probability distribution reflects how much the values of a random variable vary. Greater spread indicates more variability, while smaller spread suggests that outcomes are consistently near the center.

Spread provides essential insight into the reliability and predictability of outcomes. A narrow distribution implies less uncertainty in the population, while a wide distribution reflects greater diversity in possible values.

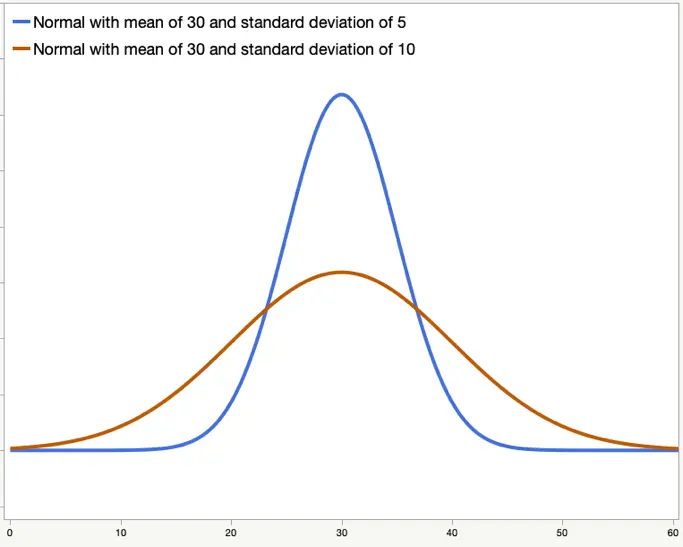
These two normal curves share the same mean but have different standard deviations, visually demonstrating how a narrow curve indicates low variability while a wider curve reflects greater spread. Although illustrated with normal distributions, the concept of spread applies to all probability distributions. Source.

Interpreting spread equips students to assess how stable or volatile outcomes may be in the long run.

Connecting Distribution Features to Population Characteristics

Interpreting probability distributions goes beyond simply labeling characteristics. Students use shape, center, and spread to draw meaningful conclusions about the population of interest.

Important interpretive goals include:

• Identifying trends suggested by how probability mass is allocated across values.

• Recognizing unusual or extreme outcomes by comparing them to the distribution's center and variability.

• Describing long-run behavior, an essential aspect of statistical interpretation grounded in relative frequency.

• Assessing population differences, especially when comparing multiple distributions.

These interpretations rely on understanding that a probability distribution is a model representing the behavior of a random variable over many repeated trials. As students learn to interpret these features, they develop the ability to make informed statements about the real-world processes and populations the distribution approximates.

Using Interpretations to Draw Statistical Conclusions

Once students understand the structure of a probability distribution, they can apply this knowledge to make conclusions supported by statistical reasoning. According to the specification, interpretations should help determine what the distribution suggests about the population. This may include identifying central tendencies, recognizing variability, or determining whether patterns imply specific characteristics of the underlying random process.

Interpreting distributions therefore serves as a bridge between abstract probability models and real-world statistical insight. Students who master these interpretive skills gain a deeper appreciation of how probability distributions guide our understanding of populations and support evidence-based conclusions.