AP Syllabus focus:
‘VAR-5.E.2: Discuss the criterion for independence between two random variables X and Y, emphasizing that knowing the outcome of one does not affect the probability distribution of the other.’
This section explains the fundamental idea of independence between random variables, showing how one variable’s behavior provides no information about the other, which is essential for probability modeling.
Understanding Independence of Random Variables
Independence plays a central role in probability because it determines whether two random variables influence each other’s outcomes. In AP Statistics, understanding independence helps students correctly compute combined probabilities and interpret the behavior of jointly considered variables such as measurements, counts, or outcomes of random processes.
What Independence Means in Probability
Two random variables are considered independent when information about the value of one variable does not change or inform the probability distribution of the other. This concept aligns with the syllabus requirement to understand independence as a condition in which knowledge of one outcome does not alter predictions or expectations for the other variable.
Independent Random Variables: Two random variables are independent if the probability distribution of one variable remains unchanged when the value of the other variable is known.
Independence implies that the variables do not share a causal link, structural relationship, or probability-based dependency. Instead, each arises from its own random process or mechanism that does not influence the other.
Probabilistic Criterion for Independence
The formal criterion for independence provides a mathematical expression of the principle that the variables do not affect each other. This criterion is frequently used in both probability theory and applied statistical analysis, including when combining random variables.
EQUATION
= Joint probability of X taking value x and Y taking value y
= Probability that X equals x
= Probability that Y equals y
This equation formalizes the idea that the combined probability of two independent outcomes equals the product of their individual probabilities.
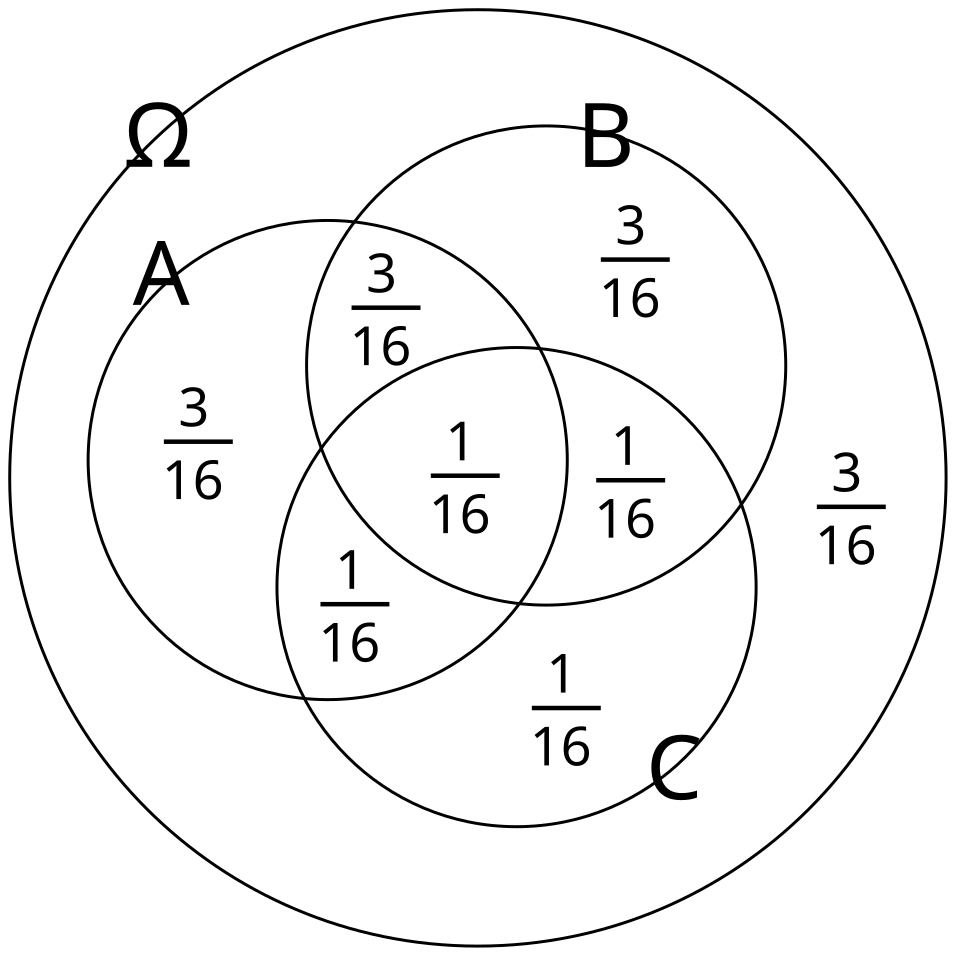
A diagram showing three mutually independent events, illustrating the principle that joint probabilities factor into products of marginal probabilities. It extends the idea of independence beyond two variables while reinforcing the same underlying concept. Source.
A sentence is needed here to maintain proper structure and avoid stacking special formatting blocks.
Why Independence Matters
Independence is essential for determining how random variables can be combined in statistical models. Many probability rules, variance formulas, and distributional results rely on independence as a prerequisite. When independence is assumed, calculations simplify, predictions become more straightforward, and the resulting probability distributions often have cleaner forms.
Recognizing Independent Random Variables
In practical statistical contexts, independence is a property of the process generating the variables rather than an observable characteristic of the data alone. Understanding this helps students avoid the common misconception that independence can always be inferred visually or directly from patterns in observed outcomes. Independence is guaranteed when variables originate from unrelated random processes such as:
Separate physical measurements not affecting each other
Repeated trials of a random mechanism meeting independence requirements
Distinct events governed by unrelated probability rules
These conditions underscore that independence must be justified based on context and reasoning about the process, not just sample results.
Distinguishing Independence from Other Relationships
Students must also distinguish independence from concepts such as:
Mutual exclusivity, which applies to events rather than random variables
Correlation, which measures linear association but does not determine independence
Causal relationships, which may involve directional influence and cannot be assumed from statistical independence
Understanding these distinctions strengthens comprehension of how independence fits within the broader landscape of probability and statistics.
The Role of Independence in Probability Distributions
Independence is particularly significant when analyzing joint distributions of random variables. When two random variables are independent:
Their joint probability distribution is the product of their marginal distributions
Each variable retains its individual distributional shape
Knowledge of one variable’s observed or theoretical value adds no predictive information about the other
These properties make independence a simplifying condition in constructing models and performing calculations.
Implications for Combining Random Variables
Although this subsubtopic focuses solely on defining and understanding independence, its implications extend to other areas of probability. Independence is required for many upcoming results in the AP Statistics curriculum, including those involving variance, linear combinations, and certain distributional models. Students should view independence as a foundational assumption that enables later computations to hold true.
Independence ensures that when combining random variables, their behaviors contribute additively or multiplicatively according to predictable rules without hidden interactions.
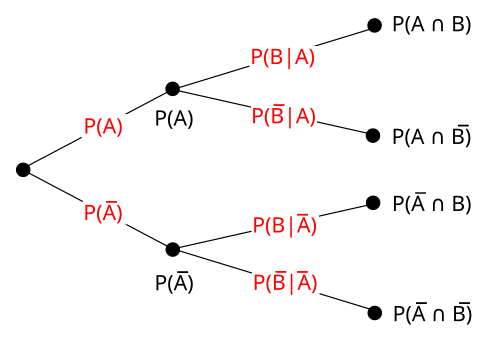
A probability tree showing how joint outcomes are formed along branching paths, with joint probabilities obtained by multiplying branch probabilities. The diagram also displays conditional structure, which extends slightly beyond the immediate focus while remaining consistent with related AP Statistics content. Source.
This understanding prepares students to analyze more complex probability structures with confidence and precision.
FAQ
When the generating processes are not explicitly described, independence is usually assessed through contextual reasoning rather than formal testing.
Analysts typically consider whether any plausible mechanism could link the variables.
If no such mechanism exists and observations do not exhibit systematic patterns, independence is often treated as a reasonable modelling assumption.
No. Apparent patterns may arise by chance, especially in small samples. Independence concerns the underlying random processes, not the observed outcomes.
Only when the pattern is consistent, structured, and explainable by a plausible link between the variables should dependence be considered.
Yes. Temporal or spatial proximity does not imply dependence.
Independence holds as long as neither measurement affects the other and they do not share a mechanism that influences their variability.
Weather, biological activity, and human behaviour are common examples where simultaneous measurements may still be independent.
Independence simplifies the modelling process because the joint distribution can be formed by multiplying separate marginal distributions.
This removes the need to model any structural link between the variables.
It also reduces the number of parameters and assumptions, making models easier to justify and interpret.
Dependence can arise when:
• The variables are influenced by the same external condition, such as temperature, demand, or population size.
• One variable directly affects the other through feedback or sequence effects.
• Both variables involve shared constraints, like limited resources or capacities.
These factors introduce structure into the joint behaviour that cannot be explained by independent processes.
Practice Questions
Question 1 (1–3 marks)
A researcher selects one student at random and records the number of hours they spent revising yesterday (random variable X). The researcher independently rolls a fair six-sided die and records the outcome (random variable Y).
a) Explain why X and Y can be considered independent random variables.
b) State the condition that must hold for two random variables to be independent.
Question 1
a) (1 mark)
• Award 1 mark for stating that X and Y arise from unrelated processes, so the outcome of one does not influence the other.
b) (1 mark)
• Award 1 mark for stating the independence condition: the joint probability of X and Y must equal the product of their individual probabilities.
(Allow full credit if phrased correctly without mathematical notation.)
Total: 2 marks
Question 2 (4–6 marks)
A wildlife biologist records the number of birds visiting a feeder during a 10-minute interval (random variable A). Independently, a motion-sensor camera records the number of squirrels passing through a nearby clearing during the same 10-minute interval (random variable B).
a) Give one reason why A and B might reasonably be treated as independent random variables in this context.
b) The biologist observes that A = 3 birds during the interval. Does this change the probability distribution of B? Explain your reasoning.
c) The joint probability P(A = 3 and B = 2) is found to equal P(A = 3) multiplied by P(B = 2). What does this indicate about the relationship between A and B?
Question 2
a) (1–2 marks)
• 1 mark for giving a reasonable explanation that birds and squirrels behave independently or are influenced by separate ecological factors.
• 1 additional mark if the explanation includes that the processes generating A and B do not affect one another.
b) (1–2 marks)
• 1 mark for stating that the distribution of B does not change when A is known if the variables are independent.
• 1 mark for explaining that knowing the number of birds does not provide information about how many squirrels pass through.
c) (1–2 marks)
• 1 mark for identifying that the equality of joint and product probabilities demonstrates independence.
• 1 mark for explicitly stating that A and B are independent random variables.
Total: 4–6 marks

