Interpreting probabilities and parameters for a sampling distribution of a sample proportion requires connecting mathematical quantities to real populations, emphasizing context, appropriate units, and clear statistical reasoning.

Interpreting Probabilities and Parameters in Sampling Distributions for Sample Proportions

Understanding how to interpret probabilities and parameters for a sampling distribution of a sample proportion is central to making valid inferences about a population. A sampling distribution describes how a sample statistic behaves across repeated random samples of the same size from the same population.

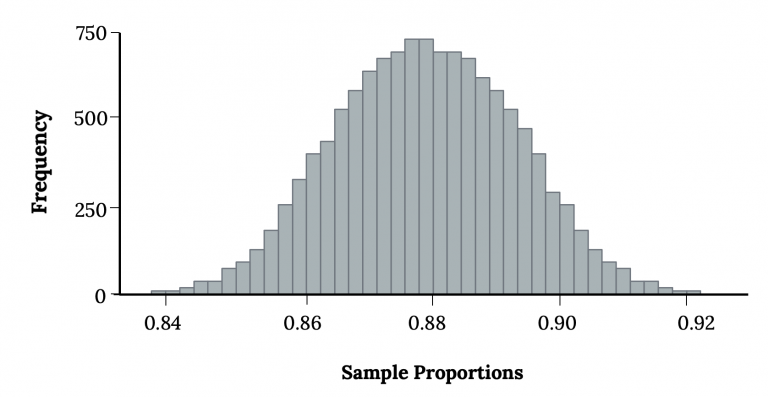
A histogram showing simulated sample proportions from thousands of random samples, illustrating how most values cluster near the true population proportion and fewer fall in the tails. Source.

When the statistic of interest is the sample proportion (written as p-hat, or $\hat{p}$), its sampling distribution allows us to attach probability-based statements to possible sample outcomes and reason about what they imply for the population proportion p.

The Role of Context in Interpretation

In AP Statistics, every probability statement must be grounded in real-world context. Because sample proportions describe categorical outcomes, such as the proportion of students who prefer online learning, each interpretation must reference the specific population and variable being studied. Without context, probabilities lose meaning and cannot guide decision-making.

Students must remember that probabilities in a sampling distribution describe the long-run relative frequency of observing particular sample proportions under repeated sampling using the same method.

Key Parameters of the Sampling Distribution of $\hat{p}$

Two parameters define the sampling distribution for a sample proportion drawn from a population with true proportion p:

• The mean of the sampling distribution, which equals p, represents the long-run center of all possible sample proportions.

• The standard deviation of the sampling distribution, sqrt(p(1-p)/n), measures how much the sample proportion is expected to vary across random samples of size n, assuming sampling with replacement or a sample size less than 10% of the population.

These parameters allow analysts to reason about how close a typical sample proportion is likely to be to the population proportion.

EQUATION

These formulas support probability interpretations by quantifying how sample proportions behave under repeated sampling.

Interpreting Probability Statements

Probability statements involving p-hat describe how likely it is to observe a sample proportion in a particular range when sampling from the population. When interpreting these statements, the following principles apply:

• Always reference the sampling method, such as taking a random sample of size n from the specified population.

• Describe the variable of interest, such as the proportion of adults who own electric vehicles.

• Avoid interpreting the probability as a guarantee for a single sample; probabilities apply to the long run, not to isolated instances.

When a normal approximation is applicable, such as when np ≥ 10 and n(1-p) ≥ 10, probabilities associated with intervals can be interpreted as areas under an approximately normal sampling distribution curve. However, the interpretation must still be contextual and focused on what sample proportions represent in the real world.

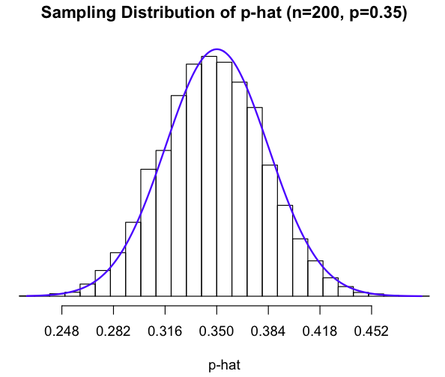
A histogram of a sampling distribution of p-hat with a superimposed normal curve, illustrating how centre and spread relate to the true proportion and sample size when normal approximation is appropriate. Source.

Using Units and Population Descriptions Appropriately

Because sample proportions represent percentages or fractions of categorical outcomes, interpretations must emphasise units such as “proportion,” “percentage,” or “fraction.” To align with AP expectations:

• Identify the population (e.g., “all voters in the state”).

• Identify the sample proportion being measured (e.g., “the sample proportion who support Policy A”).

• Maintain consistent units across all probability and parameter statements.

Incorrect interpretations often stem from omitting one of these elements or confusing sample proportions with counts.

Connecting the Theoretical Distribution to Real-World Inference

Interpreting probabilities and parameters requires understanding how the theoretical sampling distribution translates into insights about population behaviour. This connection is essential when:

• Assessing whether a sample result is typical or unusual.

• Determining whether sample evidence supports or contradicts a claim about the population proportion.

• Evaluating the strength of evidence in statistical inference procedures such as confidence intervals and significance tests.

To make this connection, probability statements must explicitly relate the behaviour of sample proportions back to the population parameter p, emphasising that observed outcomes reflect random variation inherent in sampling.

Practical Guidelines for Clear Interpretation

• Tie every probability and parameter to the context of the specific population and variable being studied.

• State parameters in population terms, not sample terms.

• Interpret probabilities as long-run frequencies, not certainties for single samples.

• Use units consistently, focusing on proportions or percentages.

• Differentiate between sample statistics and population parameters, highlighting the role of random variation.

• Frame conclusions about populations, not about individual sample members.