Understanding how to justify claims using significance test results is essential for interpreting statistical evidence and connecting numerical outcomes to meaningful conclusions about population parameters in context.

Using Test Results to Justify Claims

When conducting a one-sample t-test for a population mean, statisticians must translate numerical evidence into statements that address the original research question. This requires careful interpretation of the test outcome, focusing on whether the evidence supports or fails to support a claim about the population mean. Because sample data involve random variation, the justification of claims depends on comparing the p-value to a preselected significance level and evaluating what the result suggests about the underlying population parameter.

Understanding Claims in the Context of Hypotheses

Claims are tied to the null hypothesis and alternative hypothesis, which reflect competing statements about the population mean. The claim being evaluated may align with either hypothesis, but justification always relies on evidence from the collected sample.

A brief interval of logical reasoning separates hypotheses from conclusions. A statistical test does not prove a hypothesis true or false; instead, it evaluates whether the sample provides strong enough evidence to question the assumption made in the null hypothesis.

To justify a claim, the analyst must determine whether the test outcome supports the view expressed in the alternative hypothesis or maintains the position of the null hypothesis.

Role of the p-Value in Justifying Claims

The p-value serves as the key piece of evidence in a significance test. It quantifies how surprising the observed sample result would be if the null hypothesis were true. Lower values indicate stronger inconsistency with the null hypothesis and greater support for the alternative.

A meaningful justification requires clearly comparing the p-value to the significance level α. This threshold represents the maximum acceptable probability of mistakenly rejecting a true null hypothesis. Thus, decision-making and justification must always occur within this predetermined framework.

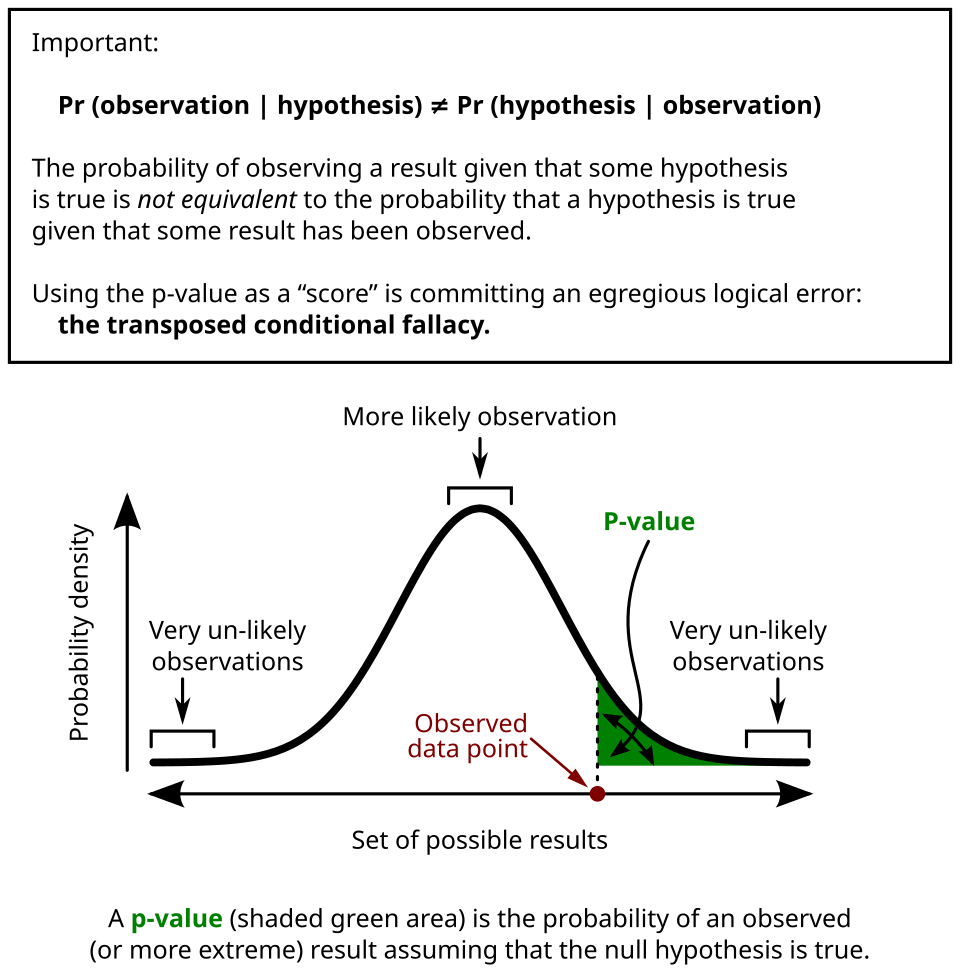
This diagram shows a null distribution with the p-value shaded in the tail, illustrating how unlikely results under the null hypothesis provide evidence supporting the alternative. The shaded tail highlights why small p-values justify rejecting H0H_0H0​. All visible text directly aligns with AP Statistics treatment of p-values. Source.

Making and Justifying Decisions Based on Test Outcomes

When interpreting test results, the reasoning must follow established statistical rules while remaining tied to the specific context of the data.

When the Null Hypothesis Is Rejected

If p ≤ α, the test supplies evidence that the sample mean differs from the hypothesized value. This does not prove the alternative hypothesis but indicates that the data are unlikely under the null model.

Key reasoning points include:

• The evidence is sufficient to support a claim that the population mean differs from $μ_0$.

• The conclusion must explicitly reference the direction of the alternative hypothesis when relevant.

• The justification must be stated in real-world terms rather than purely statistical phrasing.

When the Null Hypothesis Is Not Rejected

If p > α, the data are not surprising under the null hypothesis. Consequently, the test does not offer enough evidence to support a claim of difference.

Important considerations include:

• Failure to reject does not prove the null hypothesis true; it simply reflects insufficient evidence.

• Claims asserting a difference cannot be justified because the data do not strongly contradict $μ_0$.

• The interpretation must emphasize that conclusions are about evidence, not absolute truth.

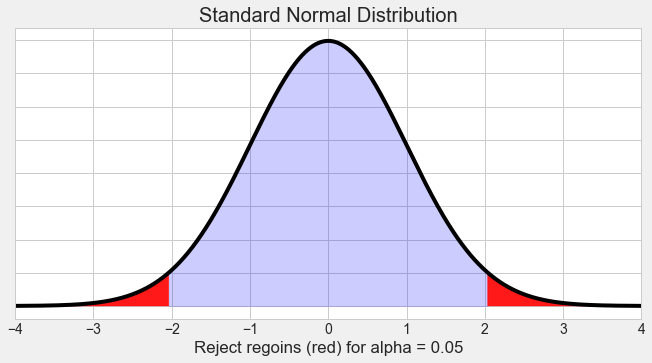
This figure illustrates a rejection region determined by the significance level, showing how a test statistic falling within the shaded tail leads to rejecting H0H_0H0​. Although drawn for a z-test, the conceptual decision rule is identical for t-tests used in AP Statistics. Source.

Connecting Statistical Evidence to Claims in Context

Justification is strongest when tied clearly to the scenario being studied. Contextualization shows how the statistical result informs real-world interpretation. Effective contextual statements should:

• Refer directly to the population and parameter of interest.

• Use phrases such as “the results provide evidence that…” when rejecting H₀.

• Use phrases such as “there is not enough evidence to conclude that…” when failing to reject H₀.

• Emphasize that conclusions depend on sample-based uncertainty and the methodology of the significance test.

Because statistical reasoning must account for inherent variability, clear and accurate communication ensures that claims are neither overstated nor misinterpreted.

Implications of the Test Outcome

The implications of a significance test extend beyond the numerical decision. Analysts must consider:

• The strength of evidence, as indicated by the magnitude of the p-value.

• The practical meaning of any detected difference, even if statistically significant.

• Whether additional data or more precise measurement may be necessary before making strong claims.

These implications help guide responsible interpretation, ensuring that claims remain rooted in the evidence produced by the sample and the assumptions underlying the significance test.