Verifying conditions for significance testing in regression ensures that statistical conclusions about the population slope are trustworthy, consistent, and supported by appropriate model assumptions.

Understanding the Purpose of Condition Checks

Before conducting a significance test for the slope of a regression model, students must confirm that the data reasonably satisfy several assumptions. These assumptions justify using the t-distribution to model sampling variability in the estimated slope. Failing to verify conditions risks inaccurate p-values, incorrect conclusions about the population slope, and misleading interpretations about the relationship between variables.

Linearity Condition

Why Linearity Matters

The significance test for the slope relies on the assumption that the true relationship between the explanatory variable x and the response variable y is linear. When this assumption holds, the estimated slope meaningfully reflects how the average value of y changes with x.

Checking Linearity

Students assess linearity primarily through residual analysis, which involves examining how residuals behave relative to the fitted regression line.

After plotting residuals versus predicted values or versus x, students look for the following indicators:

• Random scatter around zero line

• No distinct curves or patterns

• No clusters suggesting different subgroups in the data

A visible curve or systematic structure signals that a linear model may be inappropriate.

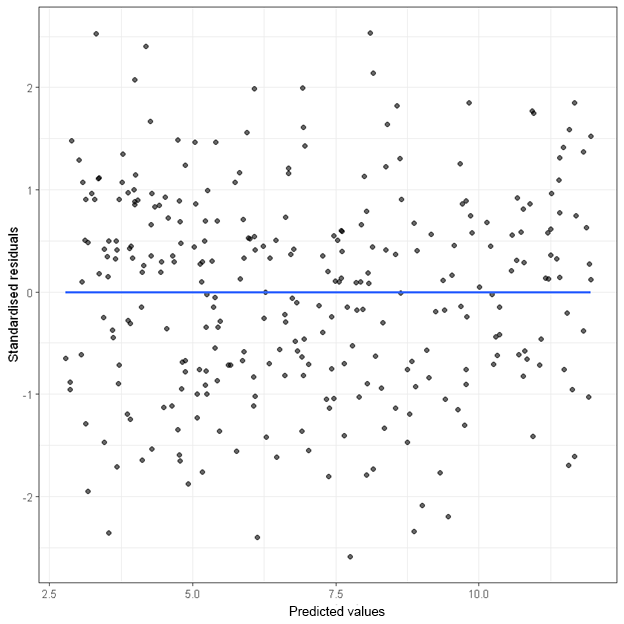
This residual plot shows a random cloud of points centered around zero, supporting both linearity and constant standard deviation assumptions. Its absence of patterns or funnel shapes indicates that the regression model is appropriate with respect to these two conditions. Source.

Constant Standard Deviation Condition

Importance of Equal Variability

The assumption of constant standard deviation (also called homoscedasticity) states that the variability in y should remain roughly the same for all values of x. If variability increases or decreases systematically, standard errors may be distorted, affecting test results.

Checking Homoscedasticity

Residual plots should show:

• Scatter that maintains a similar vertical spread across all x

• No funnel shapes (indicating increasing or decreasing spread)

• No isolated regions of large or small variance

Unequal spread, or heteroscedasticity, weakens reliability of the slope test.

Independence Condition

Why Independence Is Essential

The method for testing the slope assumes that each observation provides unique information. When observations are not independent—such as in time series without proper handling, clustered samples, or repeated measures—standard inferential methods may underestimate or overestimate variability.

Ensuring Independence

Students consider study design to justify independence:

• Random sampling from the population

• Random assignment in experiments

• Avoiding situations where one observation directly influences another

The 10% condition applies when sampling without replacement: the sample size should be less than 10% of the population to ensure approximate independence of observations.

Normality Condition

Role of Normality in Regression Testing

Significance testing for the slope assumes that for any given x, the distribution of y-values is approximately normal. This assumption is especially important when sample sizes are small, as it affects the accuracy of the sampling distribution of the slope.

Checking Normality

Students typically use:

• Histograms of residuals

• Normal probability (Q–Q) plots

• Consideration of skewness and outliers

When sample size is large (n > 30), the t-procedure becomes more robust to departures from normality, due to the central limit theorem’s effect on the sampling distribution of the slope.

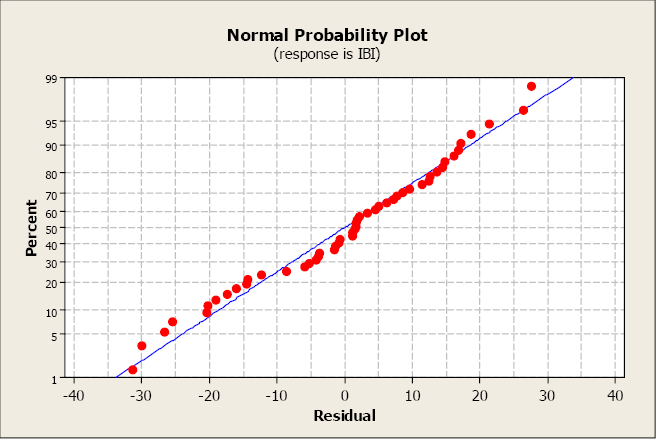
This normal probability plot illustrates how residuals that fall near a straight reference line support the normality assumption. Even though drawn from a specific ecological dataset, the diagnostic pattern applies universally to regression residual checks. Source.

Bringing Conditions Together for Valid Inference

Using Condition Checks to Support a Regression Test

Before performing a significance test for the slope, students systematically review all four conditions:

• Linearity ensures the slope has meaningful interpretation.

• Constant standard deviation maintains accurate standard errors.

• Independence validates the use of the t-distribution.

• Normality ensures reliable p-values, especially for small samples.

Meeting these conditions allows the t-test for the slope to provide valid evidence about whether the population slope differs from a hypothesized value. If any condition appears violated, students should note limitations and consider alternative models or data transformations.

This structured verification process strengthens conclusions drawn from regression analysis and reinforces statistical reasoning in evaluating relationships between quantitative variables.