Introduction

Analysing experimental results involves transforming raw observations into meaningful information. It requires careful processing, interpretation, and reasoning to ensure valid conclusions are supported by reliable data and clear scientific evidence.

Understanding Qualitative and Quantitative Results

Qualitative Results

Qualitative results are non-numerical observations that describe the qualities or characteristics of substances or reactions. These may include:

• Colour changes (e.g. blue to colourless in Cu²⁺ reduction)

• Formation of precipitates (e.g. silver chloride in halide tests)

• Effervescence indicating gas production

• Changes in odour or temperature observed during reactions

These observations are typically recorded in words and rely on descriptive accuracy and consistency. They often help to identify substances or confirm reaction mechanisms.

Quantitative Results

Quantitative results involve numerical data that can be measured, calculated, or statistically analysed. Examples include:

• Volumes of solutions in titrations

• Mass changes during thermal decomposition

• Temperature readings in enthalpy experiments

• Electrical measurements in electrochemical cells

These results allow for mathematical treatment and data processing, forming the basis for drawing numerically justified conclusions.

Processing Qualitative Data

Recording and Organisation

To ensure validity, qualitative data should be:

• Recorded immediately during the experiment to prevent bias

• Organised systematically in tables or labelled diagrams

• Described objectively, avoiding subjective terms such as “slightly” or “strongly” unless comparative context is clear

For example, instead of noting “slight colour change,” record “solution changed from pale blue to colourless.”

Interpreting Qualitative Data

Interpretation involves linking observations to chemical theory, such as recognising oxidation states, identifying ions, or inferring reaction pathways.
Common reasoning steps include:

• Linking colour changes to transition metal oxidation

• Identifying precipitation reactions as evidence of insoluble salts

• Using gas evolution to confirm decomposition or redox processes

Processing Quantitative Data

Data Organisation and Presentation

Quantitative results must be recorded with:

• Appropriate headings and units

• Consistent significant figures matching the measuring apparatus

• Clear notation distinguishing measured values from calculated ones

Data tables should include columns for raw data, processed data (e.g. mean values), and units for every column.

Data Processing Techniques

Common processing methods include:

• Averaging repeated measurements to reduce random error

• Calculating mean titres (excluding anomalies) in titration data

• Applying corrections, e.g. for zero errors on instruments

• Converting units consistently into SI form before analysis

Read liquid volumes at eye level and take the value from the bottom of a concave meniscus (or top of a convex meniscus), avoiding parallax error.

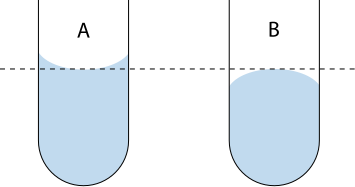
Diagram showing the correct meniscus reading for concave and convex liquids at eye level to minimise parallax error. Accurate readings underpin reliable processed values such as mean titres and uncertainties. Labels indicate the correct reference point on the curve. Source

Mathematical Treatment

This type of calculation allows students to quantify reaction efficiency and assess data reliability.

Data Interpretation and Trend Analysis

Identifying Patterns and Relationships

When processing experimental results, patterns may indicate relationships between variables, such as:

• Direct proportionality (e.g. concentration vs. rate)

• Inverse relationships (e.g. pressure vs. volume in gases)

• Curved trends suggesting non-linear dependence

Interpreting these patterns requires understanding of underlying chemical principles like collision theory or equilibrium dynamics.

Linking Data to Theoretical Models

Students must apply chemical theory to explain observations:

• Increasing temperature generally increases reaction rate due to higher kinetic energy.

• Decreasing concentration reduces rate as there are fewer collisions per unit time.

• In equilibrium studies, data trends should be related to Le Chatelier’s principle.

This stage transforms data into scientific conclusions supported by evidence.

Reliability and Data Integrity

Ensuring Reliable Data

Reliability arises from:

• Consistent techniques across repeats

• Calibration of apparatus

• Elimination of anomalous results identified through data comparison

Repeating measurements enhances precision and helps in assessing repeatability (the ability to obtain similar results under the same conditions).

Recognising Anomalies

Anomalous results deviate significantly from others and may arise due to:

• Human error (e.g. misreading volumes)

• Equipment faults (e.g. air bubbles in burette)

• Environmental factors (e.g. temperature fluctuations)

Anomalies should not be ignored but rather noted and excluded from final calculations with justification.

Record qualitative observations (e.g., colour change, precipitate formation, gas evolution) alongside conditions, as they justify processing decisions such as accepting or discarding measurements.

Photograph of an acid–base titration at the phenolphthalein endpoint in a conical flask. The pale pink colour indicates endpoint under typical alkaline conditions. This visual criterion supports consistent judgement when processing titres. Source

Statistical and Mathematical Considerations

Using Averages and Ranges

Statistical tools help summarise data trends:

• Mean gives a central value.

• Range shows data spread and indicates variability.

• Standard deviation (where appropriate) quantifies precision.

Significant Figures

Use the same number of significant figures in processed data as the least precise measurement, ensuring numerical consistency and avoiding overstatement of precision.

Uncertainty and Error Analysis

This expresses how confident the experimenter can be in a particular measurement and helps in evaluating data accuracy.

Drawing Valid Conclusions

Criteria for Valid Conclusions

A valid conclusion:

• Directly addresses the experimental aim

• Is supported by processed data and scientific reasoning

• Acknowledges uncertainties and limitations in the method

Students should avoid overgeneralising results and must justify every inference using numerical and qualitative evidence.

Integrating Evidence

To finalise conclusions:

• Combine quantitative results (e.g. yield, rate constants) with qualitative evidence (e.g. colour change)

• Cross-reference data trends with theoretical expectations

• Evaluate the degree of agreement between experiment and theory

Plot a calibration graph with correctly labelled axes and units, draw a best-fit line, then determine the gradient and intercept to extract the required relationship or constant.

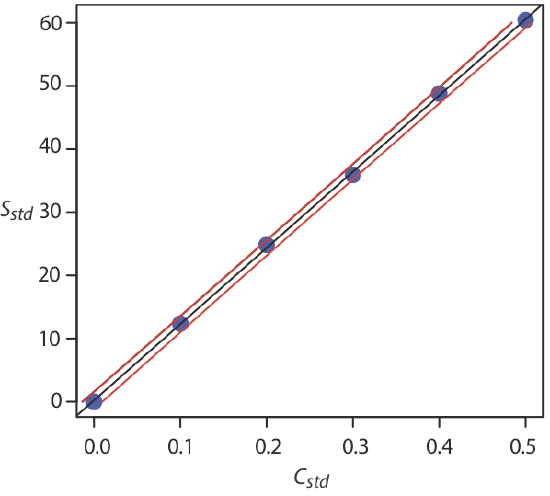
Example calibration curve with experimental points and a fitted straight line; confidence limits are shown for the analyte concentration derived from the line. This illustrates how processed data from replicates are used to obtain quantitative parameters (slope, intercept) for analysis. The plot slightly exceeds syllabus depth by showing confidence bands, but the core features (points, best-fit line, axes) are directly aligned with the specification. Source