Understanding Data Interpretation in Chemistry

In A-Level Chemistry, analysing data is central to transforming raw experimental results into meaningful scientific understanding. Students must interpret trends within data and draw justified conclusions that reflect both evidence and theory.

Recognising and Interpreting Trends

Identifying Patterns in Data

When analysing data, chemists seek relationships between independent and dependent variables. These relationships can be:

• Directly proportional: As one variable increases, the other increases proportionally.

• Inversely proportional: As one variable increases, the other decreases proportionally.

• Non-linear: The relationship follows a curve, such as exponential or logarithmic growth.

Recognising these relationships helps in explaining chemical principles, such as rate–concentration or pressure–volume relationships.

Graphical Representations

Graphs provide visual clarity in recognising trends. Students must be able to identify:

• Linear trends (straight lines) indicating constant proportionality.

• Curved trends indicating non-linear relationships.

• Plateaus or asymptotes that suggest equilibrium or saturation points.

When describing a graph, always refer to both axes, the shape of the curve, and any key features such as intercepts, maxima, or minima.

Using Graph Shapes to Explain Chemical Behaviour

Correlating Graph Shape with Theory

Each graph shape reflects an underlying chemical process or law. For example:

• A straight-line graph in a first-order reaction rate plot indicates constant proportionality between rate and concentration.

• A curve that flattens in a gas solubility plot implies the system is approaching saturation.

• Temperature–rate graphs typically rise exponentially, showing kinetic dependence on activation energy.

Understanding how theoretical models correspond to these shapes is crucial for drawing valid interpretations.

Testing Models and Theoretical Predictions

Model Validation

Once a pattern is observed, students must evaluate whether it fits a theoretical model.

• Confirmatory trends support the model (e.g., obeying Boyle’s law: P × V = constant).

• Deviations may suggest experimental errors or that assumptions in the model are invalid under the conditions tested.

Revising Theories

When significant discrepancies appear, these should prompt critical evaluation of both:

• The experimental procedure, to check for systematic error.

• The theoretical explanation, which may need refining or extension.

Drawing Justified Conclusions

Logical Reasoning

Drawing conclusions involves linking data trends with chemical reasoning. A valid conclusion must:

• Refer directly to observed data (quantitative or qualitative).

• Incorporate scientific principles that explain why the trend occurs.

• Avoid assumptions not supported by the evidence.

This requires careful integration of empirical results and theoretical understanding.

Evidence-Based Judgement

Students should support their conclusions with:

• Numerical evidence (ratios, differences, gradients).

• Graphical interpretation (e.g., slope indicating rate).

• Reference to uncertainty, where the data’s precision limits confidence in the conclusion.

Quantitative Interpretation of Trends

Using Gradients and Intercepts

In linear graphs, gradients and intercepts quantify the strength and direction of relationships.

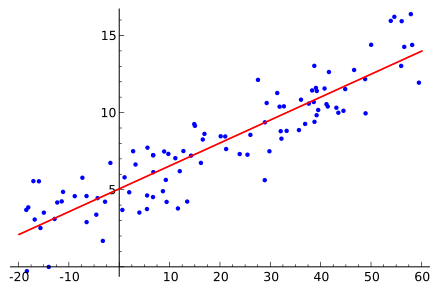
A scatter plot with a fitted line illustrates a linear trend through noisy data. The intercept shows the estimated value when the independent variable is zero, and the slope indicates the rate of change. Minor point scatter reflects experimental variability rather than a change in the underlying relationship. Source

The gradient may represent a physical quantity, such as a rate constant (k) or enthalpy change per unit.
The intercept often provides contextual information, such as the initial value of a variable.

Recognising Rate of Change

A steep gradient implies a rapid change, whereas a shallow gradient indicates a weak relationship. These distinctions are essential in topics like kinetics or thermodynamics, where small changes in variables can have large chemical implications.

Interpreting Numerical Outputs

From Raw Data to Processed Information

Processed data, such as means, ratios, or percentages, reveal numerical patterns that may not be visible in raw data. When interpreting numerical outputs:

• Compare magnitudes and ratios rather than absolute values.

• Assess whether changes are proportional, increasing, decreasing, or constant.

• Identify outliers that could distort trend recognition.

Assessing Consistency

If multiple sets of data show the same pattern, the trend is likely reliable. Consistency across replicates increases confidence that the observed relationship reflects true chemical behaviour.

Linking Trends to Chemical Concepts

Examples of Trend Interpretation

• Rates of reaction: Faster rate at higher temperature supports the collision theory due to more particles exceeding activation energy.

• Equilibrium position: Shifts predicted by Le Chatelier’s principle explain changes in concentration or pressure.

• Titration curves: The shape of the curve identifies acid–base strength and equivalence points.

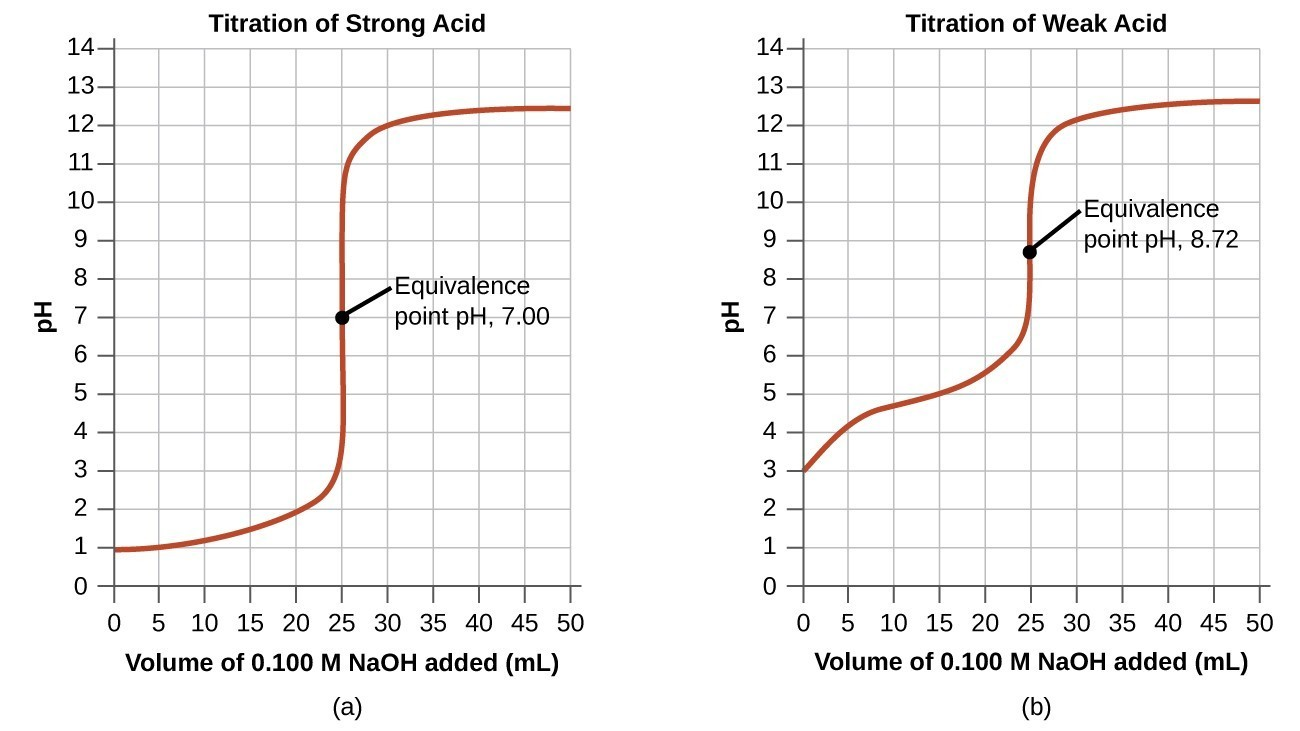
Comparative titration curves show how pH changes with volume of titrant, highlighting the equivalence point as the midpoint of the steep rise. Notation for weak vs strong systems illustrates how curve shape supports chemical conclusions. This figure includes introductory indicator context not required by the syllabus but helps visualise the steep transition region. Source

Each interpretation must connect observable data with molecular-level explanations.

Evaluating the Validity of Conclusions

Consistency and Corroboration

A strong conclusion should be:

• Consistent with all collected data.

• Corroborated by known scientific laws.

• Reproducible by other experiments under similar conditions.

Where inconsistencies appear, conclusions must be revised or qualified with uncertainty statements.

Recognising Overinterpretation

Avoid extending conclusions beyond the scope of the data. For instance, observing a linear relationship over a small range does not confirm it applies universally.

Integrating Uncertainty and Reliability

Interpreting trends must also include consideration of data uncertainty. Large uncertainties or inconsistent data reduce confidence in the trend. Students should describe how:

• Random errors affect scatter on graphs.

• Systematic errors shift the entire dataset.

• Repeat measurements improve reliability.

Conclusions should reflect both the direction of the trend and the degree of certainty with which it is known.

Key Points for Examinations

When interpreting data in written exams, ensure to:

• Describe what the data show before explaining why.

• Use quantitative references such as gradient or numerical difference.

• Always relate trends to chemical principles.

• Include any limitations or uncertainties that may weaken the conclusion.

Through systematic interpretation and critical reasoning, students can convert graphical and numerical information into scientifically robust conclusions that meet the OCR assessment objectives.