OCR Specification focus:
‘Use ΔsolH, ΔhydH and lattice enthalpy in enthalpy cycles to calculate solution energetics.’
Dissolving ionic substances involves interconnected enthalpy changes. Understanding these energy relationships allows chemists to use dissolving cycles to calculate solution energetics, linking lattice enthalpy with hydration and solution enthalpies.
Dissolving Cycles and Their Purpose
Dissolving cycles provide a structured way to analyse the energetics of dissolving an ionic solid in water. A dissolving process can be split into two conceptual steps: breaking the ionic lattice into gaseous ions and hydrating those ions in water. These steps allow the total enthalpy of solution (ΔsolH) to be linked with lattice enthalpy and hydration enthalpies (ΔhydH) through an enthalpy cycle.
When discussing dissolving cycles, it is essential to recognise that the enthalpy of solution represents the overall energy change when one mole of an ionic substance dissolves in sufficient water to form an infinitely dilute solution.
Key Enthalpy Terms in Dissolving Cycles
The dissolving process hinges on three core enthalpy changes, each contributing to the total solution energetics.
Lattice enthalpy: The enthalpy change when 1 mol of an ionic lattice forms from gaseous ions; a measure of ionic bond strength.
This enthalpy change is always exothermic for formation, but dissolving cycles require the reverse process—breaking the lattice—so the relevant step is endothermic.
A dissolving cycle also involves hydration, where water molecules interact strongly with separated ions.
Enthalpy change of hydration (ΔhydH): The enthalpy change when 1 mol of gaseous ions becomes hydrated by water molecules to form aqueous ions.
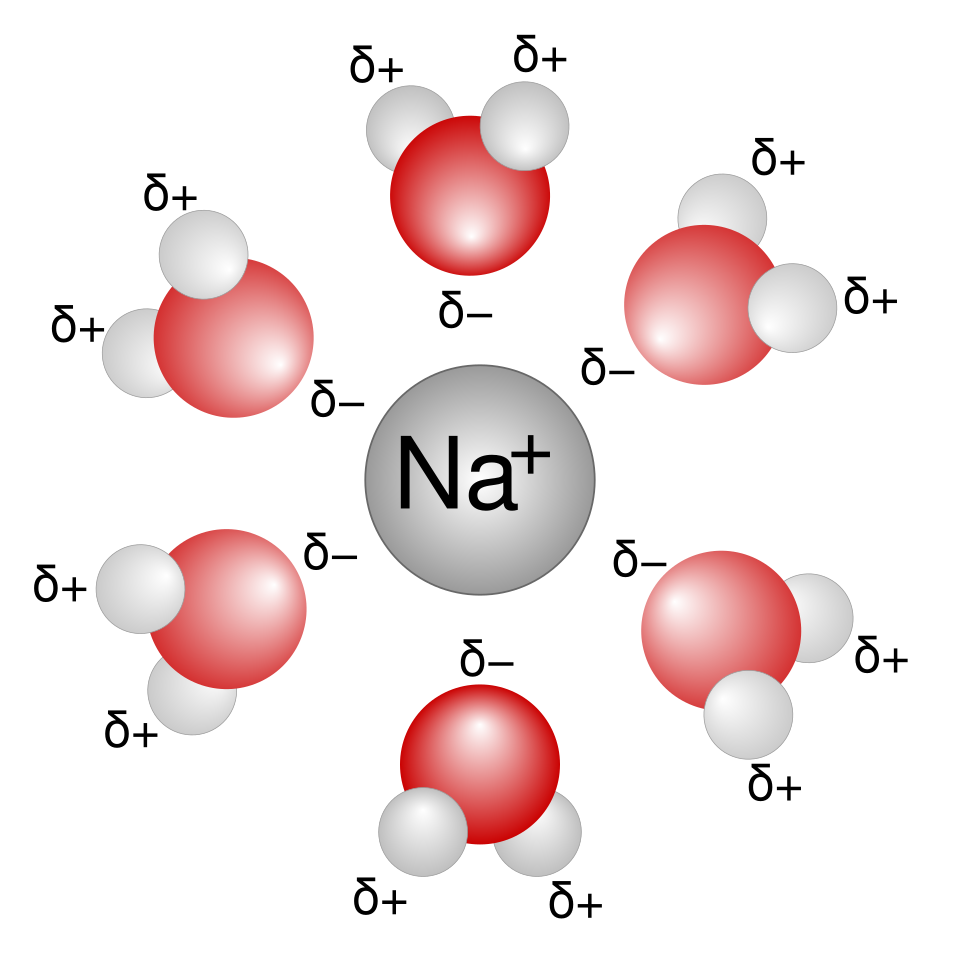
A schematic hydration shell around Na⁺, showing water molecules oriented with the oxygen end towards the cation. This orientation reflects ion–dipole attractions, which are responsible for the exothermic enthalpy of hydration. Source
Hydration enthalpies are always exothermic due to strong ion–dipole interactions.
Finally, these steps combine to give the enthalpy of solution.
Enthalpy change of solution (ΔsolH): The enthalpy change when 1 mol of an ionic substance dissolves in water to form an aqueous solution.
Between these enthalpy changes lies the core relationship governing dissolving cycles.
The Enthalpy Cycle Relationship
A dissolving cycle is a Hess cycle that links lattice enthalpy, hydration enthalpy and solution enthalpy. It allows chemists to calculate any one of the three quantities when the other two are known. Because the dissolving pathway can be conceptualised in two different ways—direct dissolution or via gaseous ions—the cycle is essential for determining otherwise inaccessible enthalpy values.
Using a Hess-style dissolving cycle, ΔsolH can be related to the lattice enthalpy and the sum of the ion hydration enthalpies.
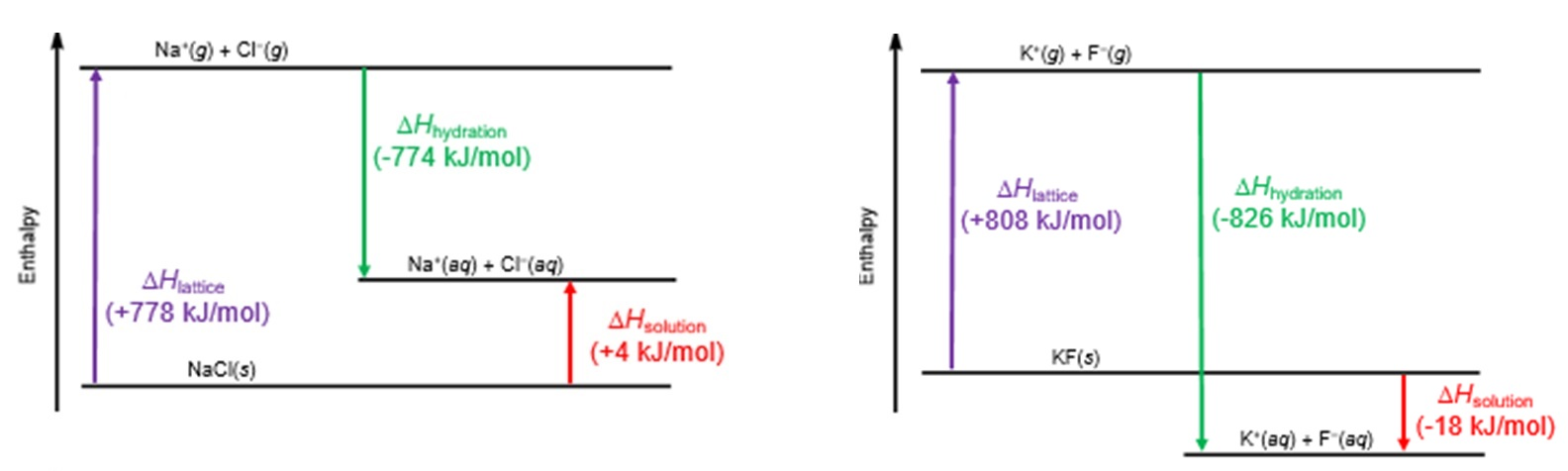
Energy-level dissolving cycles showing lattice enthalpy, hydration enthalpy, and enthalpy of solution. The diagrams illustrate how the relative magnitudes of these terms determine whether dissolving is endothermic or exothermic. Source
Dissolving Cycle Relationship (ΔsolH) = ΣΔhydH − Lattice enthalpy
ΔsolH = Enthalpy change of solution (kJ mol⁻¹)
ΔhydH = Enthalpy change of hydration for each ion (kJ mol⁻¹)
Lattice enthalpy = Enthalpy change for forming the ionic lattice from gaseous ions (kJ mol⁻¹)
This relationship applies to simple ionic solids and can be adapted for polyatomic ions, provided hydration enthalpies are available.
A dissolving cycle diagram visually represents this by placing the solid ionic lattice at the bottom, gaseous ions at the top, and aqueous ions on the side. Although such diagrams are useful, the underlying conceptual understanding is more important for accurate calculations.
Constructing a Dissolving Cycle
A dissolving cycle uses Hess’s law: the total enthalpy change for a reaction is independent of the steps taken. To construct a dissolving cycle for an ionic substance, follow a clear sequence.
Steps in Building a Dissolving Cycle
Start with the solid ionic lattice as the initial state.
Draw an upward arrow to the gaseous ions, representing the reverse of lattice enthalpy (endothermic).
From the gaseous ions, draw downward arrows to each aqueous ion, representing hydration enthalpies (exothermic).
From the ionic lattice directly to the aqueous ions, draw a single overall arrow for ΔsolH.
Apply Hess’s law to relate these enthalpy changes.
This structure ensures that the dissolving cycle correctly represents the energetics of the process, allowing direct comparison and calculation of enthalpy values.
Key Features of a Correct Dissolving Cycle
Each ion produced from the lattice has its own hydration enthalpy.
Lattice enthalpy is treated as formation in the specification; thus, dissolving cycles require reversing the sign to represent lattice breaking.
The hydration enthalpies are summed because both cations and anions must be hydrated.
The orientation of arrows must reflect the endothermic or exothermic nature of each step.
These features guarantee that the cycle is structurally valid and produces accurate enthalpy relationships.
Using Dissolving Cycles for Calculations
Dissolving cycles allow determination of ΔsolH, ΔhydH, or lattice enthalpy values. Although no worked examples are included here, students should understand the conceptual process involved in such calculations.
Important Considerations When Using Dissolving Cycles
Hydration enthalpies depend on ionic charge density.
Lattice enthalpy values must be used consistently with their sign convention.
Ensure hydration enthalpies are summed for all ions in the formula unit.
Use Hess’s law systematically to link the known and unknown quantities.
Using the Relationship Effectively
The dissolving cycle relationship is particularly useful when direct experimental determination of lattice enthalpy is not feasible. By combining hydration enthalpies and solution enthalpy, lattice enthalpy can be indirectly determined with accuracy.
Understanding dissolving cycles is vital for interpreting solution energetics and provides a foundation for later discussion of trends in lattice enthalpy and hydration enthalpy.
FAQ
An infinitely dilute solution ensures that interactions between dissolved ions are negligible.
This means the measured enthalpy change reflects only ion–water interactions, not ion–ion attractions or clustering effects.
Using this assumption allows dissolving cycles to be applied consistently and makes comparisons between different ionic compounds valid.
Hydration enthalpy is exothermic because energy is released when water molecules surround ions.
Strong ion–dipole attractions form between ions and polar water molecules, lowering the system’s energy.
The greater the charge density of the ion, the stronger these attractions and the more energy released during hydration.
When an ionic solid dissolves, both the cation and the anion interact independently with water.
Each ion releases energy as it becomes hydrated, so both contributions must be included.
Ignoring either ion would underestimate the total energy released during hydration and give an incorrect enthalpy change of solution.
Lattice enthalpy is defined as the energy released when gaseous ions form a solid lattice.
In dissolving cycles, the lattice must be broken apart into gaseous ions, which is the reverse process.
This reversal requires energy input, so the lattice enthalpy value is used with the opposite sign.
A positive enthalpy change of solution means the process absorbs energy.
However, dissolving can still occur because entropy increases as solid ions become dispersed in solution.
This increase in disorder can make the overall process favourable, even when dissolving is endothermic.
Practice Questions
An ionic solid MX dissolves in water.
Explain how lattice enthalpy and enthalpy change of hydration together determine the enthalpy change of solution for MX.
(2 marks)
States that the enthalpy change of solution depends on the balance between lattice enthalpy and hydration enthalpy. (1 mark)
Explains that hydration enthalpy releases energy while breaking the lattice requires energy, and the difference between these determines whether ΔsolH is positive or negative. (1 mark)
An ionic compound dissolves in water to form aqueous ions.
(a) Describe, using an enthalpy cycle, how lattice enthalpy, enthalpy change of hydration and enthalpy change of solution are related.
(b) Explain why the enthalpy change of solution for some ionic compounds is exothermic, while for others it is endothermic.
(5 marks)
(a) Relationship using an enthalpy cycle (3 marks)
Describes lattice enthalpy as the energy change involved in forming or breaking the ionic lattice from gaseous ions. (1 mark)
Describes hydration enthalpy as the energy released when gaseous ions become hydrated to form aqueous ions. (1 mark)
Correctly links these to enthalpy change of solution using a Hess-style dissolving cycle, stating that ΔsolH equals the sum of hydration enthalpies minus the lattice enthalpy. (1 mark)
(b) Explanation of exothermic vs endothermic dissolution (2 marks)
States that dissolution is exothermic when the total hydration enthalpy is greater in magnitude than the lattice enthalpy. (1 mark)
States that dissolution is endothermic when the lattice enthalpy is greater in magnitude than the total hydration enthalpy. (1 mark)

