OCR Specification focus:
‘Resistivity of metals typically increases with temperature; semiconductors show the opposite trend.’
Temperature Dependence: Metals vs Semiconductors
Temperature affects how easily electrons move through materials. Understanding how resistivity changes with temperature helps explain the contrasting electrical behaviours of metals and semiconductors in practical circuits.
Understanding Resistivity
Resistivity (ρ) describes how strongly a material opposes the flow of electric current. It depends on both the material’s intrinsic properties and environmental factors such as temperature.
Resistivity (ρ): The measure of a material’s opposition to electric current flow, independent of its dimensions. It determines how well a substance conducts electricity.
The relationship between a material’s resistance (R), resistivity (ρ), length (L), and cross-sectional area (A) is given by:
EQUATION
—-----------------------------------------------------------------
Resistance of a Conductor (R) = ρL/A
R = Resistance (Ω)
ρ = Resistivity (Ω m)
L = Length of conductor (m)
A = Cross-sectional area (m²)
—-----------------------------------------------------------------
Resistivity varies with temperature because the number and mobility of charge carriers and the degree of atomic vibration (lattice scattering) change as materials heat or cool.
Metals: Increasing Resistivity with Temperature
Metals contain a large number of free electrons that form a “sea of delocalised electrons” around fixed positive ions. These electrons are the charge carriers responsible for electrical conduction.
As temperature rises:
The metal lattice ions vibrate more vigorously, increasing electron–ion collisions.
These collisions impede the motion of free electrons, reducing their drift velocity.
Consequently, the resistivity increases almost linearly with temperature for most metals within a moderate temperature range.
Ohmic Conductor: A material whose current–voltage (I–V) relationship is linear and follows Ohm’s law, provided the temperature remains constant.
Since metallic resistivity increases with temperature, even ohmic conductors deviate from ideal linearity when heated significantly. This is important in precision circuits, where temperature control is necessary.
The relationship between a metal’s resistivity and temperature can be expressed as:
EQUATION
—-----------------------------------------------------------------
Temperature Dependence of Resistivity: ρ = ρ₀[1 + α(T – T₀)]
ρ = Resistivity at temperature T (Ω m)
ρ₀ = Resistivity at reference temperature T₀ (Ω m)
α = Temperature coefficient of resistivity (°C⁻¹)
T, T₀ = Temperatures (°C or K)
—-----------------------------------------------------------------
This positive temperature coefficient (α) indicates that resistivity increases with temperature. For metals such as copper and aluminium, α is approximately 4 × 10⁻³ °C⁻¹, meaning even small temperature rises can noticeably change resistivity.
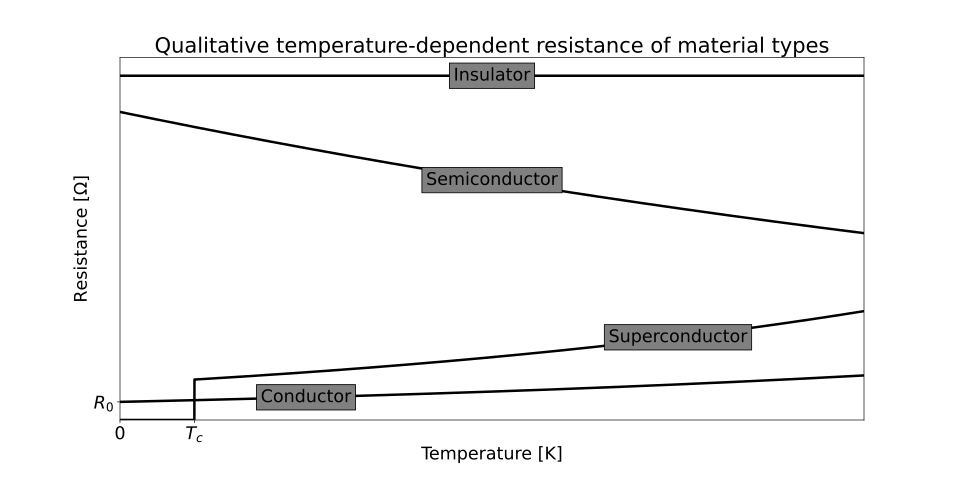
Qualitative sketch of resistance vs temperature for different material types: metals rise with temperature (positive coefficient) whereas semiconductors fall (negative coefficient). The superconductor line (drop to zero) is included on the source graphic but is beyond this OCR sub-subtopic. Use the metal and semiconductor curves to visualise the opposing trends discussed. Source.
In practical terms:
Power lines are made of metals with low α to minimise resistance increases.
Thermal management in metal components prevents overheating and excessive resistivity growth.
Semiconductors: Decreasing Resistivity with Temperature
Semiconductors such as silicon and germanium behave very differently. At low temperatures, few charge carriers are available, and they act almost like insulators. However, as temperature increases:
Thermal energy excites electrons from the valence band into the conduction band.
The number of free charge carriers (electrons and holes) increases exponentially.
Even though lattice vibrations increase, the surge in charge carriers greatly outweighs the scattering effect.
As a result, the resistivity decreases with increasing temperature.
Intrinsic Semiconductor: A pure semiconductor material where charge carriers arise solely from thermal excitation across the band gap.
This negative temperature dependence gives semiconductors a negative temperature coefficient (NTC) of resistivity.
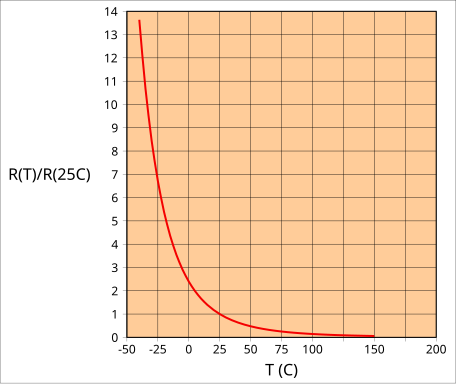
NTC thermistor R–T curve: resistance is higher than R₍₂₅°C₎ below 25 °C and lower than R₍₂₅°C₎ above 25 °C, illustrating a negative temperature coefficient typical of semiconductors. This aligns with the syllabus statement that semiconductor resistivity decreases as temperature increases. The diagram is intentionally simple, with minimal labels for clarity. Source.
EQUATION
—-----------------------------------------------------------------
Temperature Dependence (Simplified): ρ ∝ e^(E₉ / 2kT)
ρ = Resistivity (Ω m)
E₉ = Band gap energy (J)
k = Boltzmann constant (1.38 × 10⁻²³ J K⁻¹)
T = Absolute temperature (K)
—-----------------------------------------------------------------
Although the relationship is exponential rather than linear, the general trend is clear: as temperature increases, resistivity decreases.
Comparing Metals and Semiconductors
Nature of Charge Carriers
Metals: Fixed number of free electrons; conductivity determined mainly by mobility.
Semiconductors: Number of charge carriers changes significantly with temperature; mobility also changes but is less dominant in the overall effect.
Temperature Coefficient
Metals: Positive temperature coefficient (α > 0).
Semiconductors: Negative temperature coefficient (α < 0).
Microscopic Mechanism
Metals: Heating increases ion vibrations, leading to more scattering events and reduced current flow.
Semiconductors: Heating increases carrier concentration dramatically, enabling greater current flow even with more scattering.
Graphical Behaviour
Metal: Resistivity–temperature graph slopes upwards, nearly linear.
Semiconductor: Resistivity–temperature graph slopes downwards, strongly non-linear (steep at low temperatures).
Practical Significance
Understanding the temperature dependence of resistivity allows engineers and physicists to design temperature-sensitive components and stable conductors.
Applications in Metals
Copper and aluminium wiring: Chosen for low resistivity and small temperature coefficient to ensure consistent current delivery.
Resistance thermometers: Use metals like platinum, where resistivity increases predictably with temperature to measure heat precisely.
Applications in Semiconductors
Thermistors: Specifically designed semiconductors whose resistance varies with temperature; NTC thermistors decrease resistance as temperature rises.
Temperature sensors and compensation circuits: Exploit the steep negative temperature coefficient for feedback and control systems.
Integrated circuits: Semiconductor behaviour influences thermal management and performance in microelectronics.
Key Points for OCR Study
Metals show increased resistivity with temperature due to enhanced lattice vibrations.
Semiconductors show decreased resistivity with temperature because of greater charge-carrier generation.
The dominant mechanism in metals is scattering, while in semiconductors it is carrier excitation.
Recognise terms positive temperature coefficient (PTC) for metals and negative temperature coefficient (NTC) for semiconductors.
Graphs, equations, and reasoning must reflect these opposing trends clearly in OCR practical and written assessments.
FAQ
Impurities increase the overall resistivity of metals by scattering electrons, even at low temperatures. This introduces a residual resistivity that does not depend on temperature.
At higher temperatures, both impurity scattering and lattice vibrations affect resistivity, but the temperature coefficient (α) remains roughly constant. Pure metals show a stronger temperature dependence than alloys because impurities dominate scattering in alloys, reducing the relative impact of temperature changes.
The exponential relationship arises from the band gap energy between the valence and conduction bands.
As temperature increases, the number of electrons with sufficient energy to cross the band gap rises exponentially, greatly increasing charge carrier density.
Mathematically, carrier concentration n ∝ e^(-Eg/2kT), so resistivity ρ ∝ 1/n gives ρ ∝ e^(Eg/2kT). This explains the steep decrease in resistivity seen in intrinsic semiconductors with temperature.
While the number of charge carriers increases with temperature, their mobility actually decreases.
Higher temperatures cause stronger lattice vibrations, increasing scattering events that impede carrier motion.
However, in intrinsic semiconductors, the rise in charge carrier density is far greater than the drop in mobility, so overall conductivity still increases and resistivity falls. In doped semiconductors, mobility effects can become more significant at higher temperatures.
No, the temperature coefficient varies between metals.
Good conductors such as copper and silver have a relatively small coefficient (around 4 × 10⁻³ °C⁻¹), meaning resistivity rises modestly with temperature.
Metals with more complex atomic structures or stronger electron–phonon interactions, like iron or tungsten, have higher coefficients.
These differences arise from variations in electron density, atomic mass, and how easily the lattice structure vibrates when heated.
Semiconductors show large resistivity changes for small temperature variations because of their narrow band gaps and temperature-dependent carrier generation.
In metals, free electrons are already abundant, so temperature mainly affects scattering, producing gradual resistivity changes.
In semiconductors, a small temperature rise dramatically increases the number of mobile electrons and holes, greatly boosting conductivity. This sensitivity makes materials like thermistors ideal for temperature-sensing applications.
Practice Questions
Question 1 (2 marks)
Explain why the resistivity of a metal increases as its temperature rises.
Mark scheme:
1 mark for stating that increasing temperature causes metal ions to vibrate more (increased lattice vibrations).
1 mark for stating that this leads to more frequent collisions between electrons and ions, reducing electron mobility and increasing resistivity.
Question 2 (5 marks)
The resistivity of a semiconductor decreases as its temperature increases, while the resistivity of a metal increases with temperature.
Discuss the reasons for these opposite trends in terms of charge carriers and atomic behaviour.
Mark scheme:
1 mark for stating that in metals, the number of free electrons remains approximately constant with temperature.
1 mark for explaining that increasing temperature causes greater ion vibrations, which lead to more collisions and thus higher resistivity.
1 mark for stating that in semiconductors, the number of charge carriers increases significantly with temperature due to thermal excitation of electrons across the band gap.
1 mark for noting that this increase in charge carriers outweighs the effect of increased collisions, so overall resistivity decreases.
1 mark for correctly using or referring to terms such as “positive temperature coefficient” for metals and “negative temperature coefficient” for semiconductors.

