OCR Specification focus:
‘Resistivity ρ relates to resistance by R = ρL/A for a uniform conductor.’
Resistivity links a material’s intrinsic electrical properties to measurable resistance, explaining how length, cross-section, and material composition determine current flow through a conductor.
Understanding Resistivity
Resistivity is a fundamental property that determines how strongly a material opposes the flow of electric current. It allows comparisons between materials regardless of their size or shape, making it central to understanding why some substances conduct electricity efficiently while others are insulators.
Resistivity (ρ): The intrinsic property of a material that quantifies how strongly it resists current flow, independent of its dimensions.
Every conductor or semiconductor exhibits a characteristic resistivity at a specific temperature. Metals generally have low resistivity, meaning they allow current to flow easily, while insulators such as rubber or glass have very high resistivity.
Resistivity depends on the atomic structure of the material and the mobility of charge carriers, typically electrons. The easier electrons move through the atomic lattice, the lower the resistivity.
Relationship Between Resistance and Resistivity
To apply resistivity practically, we use the relationship between resistance, resistivity, length, and cross-sectional area.
EQUATION
—-----------------------------------------------------------------
Resistance of a uniform conductor (R) = ρL / A
R = Resistance (ohms, Ω)
ρ = Resistivity (ohm-metre, Ω m)
L = Length of the conductor (metres, m)
A = Cross-sectional area of the conductor (square metres, m²)
—-----------------------------------------------------------------
This relationship shows that resistance is directly proportional to length and inversely proportional to cross-sectional area. The longer the conductor, the more difficult it is for charge to pass through, and the thinner it is, the greater the resistance. The resistivity term ensures that the calculation reflects the specific material being used.
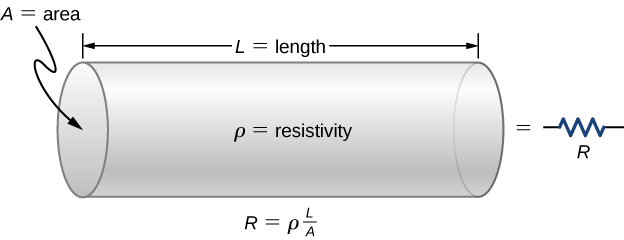
A resistor modelled as a uniform cylinder of length L and cross-sectional area A. The diagram visualises why resistance increases with length and decreases with area for a given material resistivity ρ. This directly supports the relation R = ρL/A. Source.
Between any two definition or equation blocks, it is crucial to understand the practical consequences of this relationship. Engineers and physicists use this equation to design electrical wiring, select materials for resistors, and evaluate how dimensions affect circuit performance.
Physical Meaning of the Variables
Each quantity in the equation plays a clear role:
Resistance (R) is the measurable opposition to current flow in a specific component.
Resistivity (ρ) is the fixed material constant that defines how the substance behaves electrically.
Length (L) determines how far charge must travel through the conductor; a longer path means more collisions and greater resistance.
Cross-sectional area (A) determines how much space charge carriers have to move; a wider conductor provides less resistance.
These variables together explain why wires carrying high currents are made thicker and shorter: to minimise resistance and heat loss.
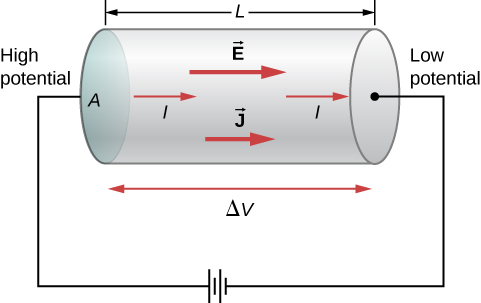
A battery drives current through a conductor segment of length L and cross-section A, illustrating how geometry controls resistance via R = ρL/A. The labels make the role of L and A explicit. (Extra detail: the figure also shows E and J; these are not required by the OCR subsubtopic but are consistent with the discussion.) Source.
Microscopic Interpretation
At the microscopic level, resistivity is governed by the motion of charge carriers (electrons) through the atomic lattice. In a metal, electrons move freely in a "sea" of delocalised charges. As they drift under an applied potential difference, they collide with vibrating atoms, losing kinetic energy and producing heat. The frequency of these collisions determines the resistivity.
For semiconductors, the situation is different: the number of charge carriers changes significantly with temperature or impurity concentration. This makes their resistivity more variable and often much higher than metals at room temperature.
Units and Measurement
The SI unit of resistivity is the ohm-metre (Ω m). This indicates the resistance of a one-metre cube of the material when current passes between opposite faces. Materials with resistivities around 10⁻⁸ Ω m (such as copper or aluminium) are excellent conductors, while values above 10⁶ Ω m indicate insulators.
When measuring resistivity experimentally, maintaining a constant temperature is essential. Resistivity typically increases with temperature in metals, because atomic vibrations intensify, causing more frequent electron collisions. In contrast, semiconductors usually show the opposite trend.
Practical Implications
Resistivity determines how materials are chosen for electrical and electronic applications:
Conductors like copper, aluminium, and silver are used in wiring due to low resistivity and high conductivity.
Alloys such as nichrome are used in heating elements, as their higher resistivity converts electrical energy into heat effectively.
Semiconductors like silicon are employed where controlled conductivity is required, such as in sensors or diodes.
This property also guides design choices for power distribution, ensuring that transmission lines have low resistivity to reduce energy loss, while components like resistors have controlled, stable resistivity values to regulate current.
Experimental Considerations
When determining resistivity experimentally, students often measure the resistance of a wire of known length and diameter. The process typically involves:
Measuring length (L) using a metre rule or digital caliper.
Determining diameter (d) to calculate the cross-sectional area using A = πd²/4.
Measuring resistance (R) using a digital ohmmeter or through voltage and current readings.
Calculating resistivity (ρ) using the rearranged form ρ = RA/L.
In real experiments, it is vital to consider uncertainties in length, diameter, and resistance readings. Small percentage errors in diameter can significantly affect the calculated area and hence the resistivity.
Key Concept Links
Understanding resistivity is essential for linking the microscopic world of electron motion to macroscopic electrical measurements. It provides a bridge between current, voltage, and material behaviour, forming the basis for topics such as:
Temperature dependence of conductors and semiconductors.
Resistivity in practical materials and their temperature coefficients.
Power loss due to resistance in electrical circuits.
By mastering the relationship R = ρL/A, students can interpret how material properties and geometry influence electrical performance, enabling them to design and analyse circuits accurately and efficiently.
FAQ
Resistivity can also vary with impurities, mechanical strain, and the crystal structure of the material.
Impurities: Adding atoms of a different element (e.g., in alloys) disrupts the electron flow, increasing resistivity.
Mechanical strain: Stretching or compressing a material changes atomic spacing, slightly altering resistivity.
Crystal defects: Imperfections or dislocations scatter electrons more, raising resistivity.
Environmental factors such as oxidation or corrosion can also modify a conductor’s effective resistivity over time.
Resistance depends on both the size and shape of a conductor, making it unsuitable for comparing intrinsic material properties.
Resistivity, however, removes those geometric effects because it standardises measurements to a specific length and cross-sectional area.
This means that two samples made from the same material, regardless of dimensions, will have the same resistivity if measured at the same temperature.
In metals, electrons move through a regular lattice of positive ions. The uniform spacing allows electrons to travel with minimal scattering.
If the lattice becomes distorted—due to impurities, deformation, or temperature increase—electrons scatter more frequently.
Increased scattering reduces mean free path, which in turn increases resistivity. The degree of lattice order is therefore critical in determining a material’s electrical performance.
In semiconductors, resistivity decreases as temperature rises, which is the opposite of metals.
This happens because increasing temperature frees more electrons and holes to act as charge carriers, increasing conductivity.
In metals, charge carrier density remains roughly constant, so higher temperatures mainly cause more collisions, raising resistivity.
Resistivity measures how much resistance a one-metre cube of material offers between opposite faces.
From the equation R = ρL / A, the units of ρ are derived as:
ρ = R × A / L = (Ω) × (m²) / (m) = Ω m
This shows that the ohm-metre expresses resistance per unit length per unit area — a natural and consistent way to quantify how materials resist current flow.
Practice Questions
Question 1 (2 marks)
A copper wire has a uniform cross-sectional area. Explain how the resistance of the wire changes if its length is doubled while keeping the material and cross-sectional area the same.
Mark scheme:
States that resistance is directly proportional to length. (1 mark)
Explains that doubling the length doubles the resistance because electrons must travel twice as far, leading to twice as many collisions. (1 mark)
Question 2 (5 marks)
A student measures the resistance of a uniform nichrome wire of length 0.80 m and cross-sectional area 1.5 × 10⁻⁷ m². The resistance is found to be 9.6 Ω.
(a) Calculate the resistivity of nichrome. (3 marks)
(b) Explain how the resistivity of the wire would change if the temperature of the wire increased significantly. (2 marks)
Mark scheme:
(a)
States or uses the correct equation R = ρL / A. (1 mark)
Rearranges to ρ = RA / L. (1 mark)
Substitutes values correctly and obtains ρ = (9.6 × 1.5 × 10⁻⁷) / 0.80 = 1.8 × 10⁻⁶ Ω m. (1 mark)
(b)
States that resistivity of metals increases with temperature. (1 mark)
Explains that as temperature rises, metal ions vibrate more strongly, increasing electron–ion collisions and reducing electron mobility. (1 mark)

