OCR Specification focus:
‘Define displacement, amplitude, wavelength, period, phase difference, frequency, and wave speed.’
Understanding the key quantities of wave motion is essential to describe and analyse how energy travels through space and matter. Each quantity provides insight into different aspects of a wave’s behaviour, allowing scientists and engineers to predict, measure, and manipulate wave phenomena effectively.
Displacement and Amplitude
Displacement
Displacement: The distance and direction of a point on the wave from its equilibrium position at a given instant.
Displacement describes the instantaneous position of a particle or point relative to the wave’s equilibrium or rest position. It can be positive or negative depending on the direction of motion relative to equilibrium. For example, in a transverse wave on a string, displacement is measured vertically; in a longitudinal wave, it is measured along the direction of propagation.
The displacement of a point varies continuously with time and position, forming the characteristic oscillatory motion of a wave.
Amplitude
Amplitude: The maximum displacement of a point on the wave from its equilibrium position.
Amplitude represents the wave’s energy and intensity — larger amplitudes indicate more energy being transferred. For sound waves, higher amplitudes correspond to louder sounds; for light waves, greater amplitude produces brighter light. Amplitude remains constant for an ideal progressive wave in a uniform medium, though it may decrease in practice due to energy loss from absorption or spreading.
Amplitude is the maximum displacement from equilibrium; wavelength λ is the distance between equivalent points on adjacent cycles (e.g. crest-to-crest).
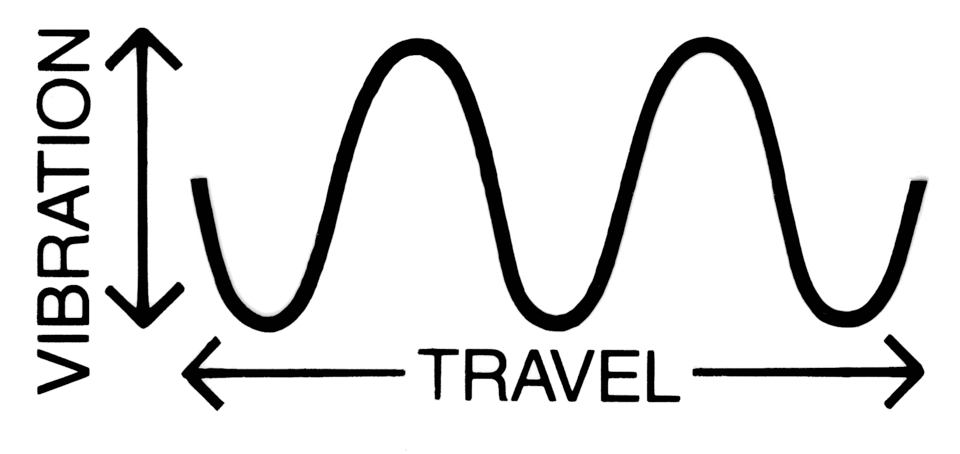
A transverse sinusoidal wave with amplitude measured from equilibrium to crest and wavelength measured between successive crests. The vertical arrow indicates particle displacement perpendicular to the direction of wave travel. Labels follow OCR usage for amplitude and wavelength. Source.
Wavelength and Period
Wavelength
Wavelength (λ): The shortest distance between two points that are in phase on a wave, such as two consecutive crests or compressions.
Wavelength is a spatial measurement, determining the length of one complete wave cycle. It is crucial in identifying the type and energy of a wave. For example, in the electromagnetic spectrum, different wavelengths correspond to different regions such as radio, visible, and gamma rays.
Wavelength can be measured directly using interference patterns or by observing successive peaks on a wave graph.
In a longitudinal wave, compressions are high-density regions and rarefactions are low-density regions; λ is compression-to-compression (or rarefaction-to-rarefaction) spacing.
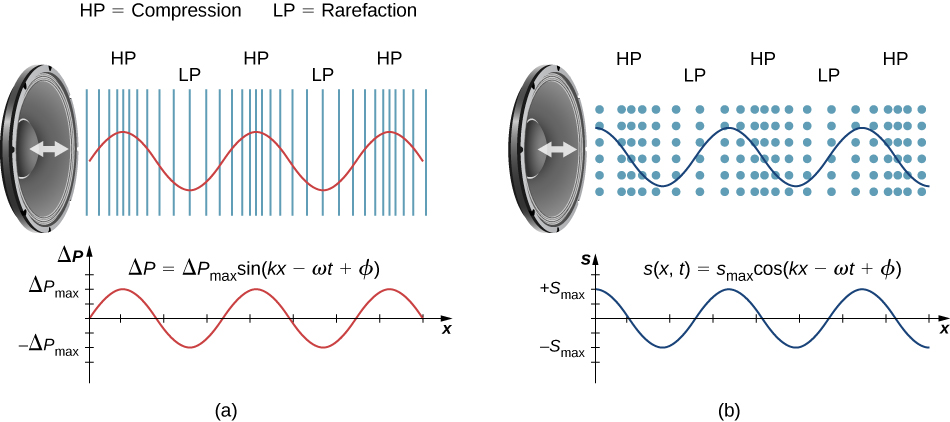
Compressions and rarefactions produced by a speaker form a longitudinal wave. The red curve plots gauge pressure versus position, aligning crests with compressions; the blue curve shows particle displacement, which is zero at equilibrium and 90° out of phase with pressure. This clarifies how wavelength, displacement, and frequency are represented in longitudinal waves. Source.
Period
Period (T): The time taken for one complete wave cycle to pass a fixed point or for one oscillation to occur.
The period provides a temporal measure of wave motion. It tells us how long each cycle lasts, linking directly to frequency — the number of cycles per second. Shorter periods correspond to higher frequencies, meaning the oscillations occur more rapidly. The period is fundamental to time-based wave analysis, especially when using oscilloscopes or time-domain graphs.
Frequency and Wave Speed
Frequency
Frequency (f): The number of complete oscillations or cycles passing a fixed point per second.
Frequency is measured in hertz (Hz), where one hertz equals one cycle per second. It determines the pitch of a sound wave and the colour of light in electromagnetic waves. Frequency and period are inversely related, providing a powerful link between time and motion in wave analysis.
EQUATION
—-----------------------------------------------------------------
Time–Frequency Relationship
f = 1 / T
f = Frequency (Hz)
T = Period (s)
—-----------------------------------------------------------------
Frequency remains constant when a wave passes between media, even though the wavelength and speed may change. This constancy makes it a reliable property for identifying waves across boundaries.
Wave Speed
Wave speed (v): The distance travelled by a wave per unit time.
Wave speed determines how quickly the energy or disturbance propagates through a medium. It depends on the properties of the medium — for example, sound travels faster in solids than in gases due to differences in particle spacing and bonding strength.
EQUATION
—-----------------------------------------------------------------
Wave Speed Equation
v = fλ
v = Wave speed (m s⁻¹)
f = Frequency (Hz)
λ = Wavelength (m)
—-----------------------------------------------------------------
This relationship links the spatial and temporal characteristics of waves, forming a foundation for most wave-related calculations in physics. For electromagnetic waves in a vacuum, the wave speed equals the speed of light (c), approximately 3.00 × 10⁸ m s⁻¹.
Phase and Phase Difference
Phase
Phase: A measure of the position of a point within a wave cycle, expressed as an angle (in radians or degrees) or as a fraction of the cycle.
Phase describes the state of oscillation of a particle or point at a given moment, allowing comparisons between different points on a wave or between different waves. Two points are in phase when they are at the same stage of their oscillation and out of phase when they differ by part of a cycle.
Phase Difference
Phase difference: The difference in phase angle between two points or two waves at a given instant.
Phase difference indicates how synchronised two oscillations are. A phase difference of 0 means perfect alignment (in phase), while a phase difference of π radians (180°) means one wave is at its crest when the other is at its trough. Understanding phase difference is essential in explaining interference, superposition, and standing wave formation — though these are explored in later subtopics.
Phase difference describes how far one oscillation is shifted relative to another, measured in degrees or radians (e.g. 90° or π/2).
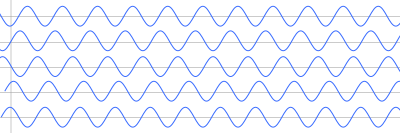
Five sine waves sharing the same frequency and amplitude but different phase illustrate what a phase offset looks like horizontally. Reading the horizontal shift at a given vertical level visualises phase difference. This supports OCR’s emphasis on relating phase to other wave quantities. Source.
Phase difference can also be related to path difference when waves travel different distances to reach the same point, a concept applied in double-slit and diffraction experiments.
Relationships and Practical Relevance
The key quantities work together to provide a complete description of a wave:
Displacement shows where particles are at any instant.
Amplitude indicates the wave’s energy.
Wavelength and frequency define its spatial and temporal characteristics.
Phase and phase difference allow comparison between oscillations.
Wave speed connects spatial and temporal measurements through the fundamental relationship v = fλ.
In practical physics, these parameters are measured using devices such as oscilloscopes for electrical signals, ripple tanks for water waves, and laser interference setups for light waves. A clear understanding of these fundamental quantities allows accurate interpretation of both experimental data and natural wave behaviour, forming the foundation for more advanced study in the topics of interference, diffraction, and stationary waves.
FAQ
Amplitude depends on the amount of energy supplied to the wave source. For instance, striking a guitar string harder transfers more energy, increasing amplitude and thus loudness.
In mechanical systems, amplitude may decrease over time due to damping, where energy is lost to friction or air resistance.
In electromagnetic waves, amplitude is linked to the strength of the electric field, determining light intensity.
Wavelength can be measured using several methods depending on the wave type:
Water waves: Use a ripple tank with a ruler or stroboscope to freeze motion and measure crest-to-crest spacing.
Sound waves: Use a microphone and oscilloscope to record the waveform and measure the distance between peaks.
Light waves: Employ interference methods, such as double-slit or diffraction gratings, to calculate λ from fringe spacing.
Each technique ensures accuracy by relating distance, phase, or interference to the wave’s repeating pattern.
Wave speed depends on the medium’s properties, such as density, elasticity, and particle spacing.
In mechanical waves, particles in denser but more elastic materials can transfer vibrations faster, as in sound travelling quicker in solids than in gases.
In electromagnetic waves, speed changes because of the material’s refractive index, where n = c / v.
The wave’s frequency remains constant, but wavelength changes to maintain the relationship v = fλ.
A phase difference exceeding 360° (or 2π radians) simply indicates that one wave has completed one or more full cycles more than the other.
Because wave motion is periodic, phase differences repeat every full cycle.
For example, a 540° phase difference is equivalent to 180°, meaning the two points are still half a cycle out of phase. Such values are often simplified by taking them modulo 360° for clarity.
No. When two waves have different frequencies, their relative phases continually change over time.
The faster oscillating wave completes more cycles per second, causing the phase difference to vary continuously.
Only waves with identical frequencies can maintain a constant phase difference, making them coherent.
This principle is crucial for producing stable interference patterns and explains why incoherent light sources do not generate visible interference fringes.
Practice Questions
Question 1 (2 marks)
A water wave travels at a speed of 2.0 m s⁻¹ and has a wavelength of 0.50 m.
(a) Calculate the frequency of the wave.
(b) State what is meant by the term amplitude of a wave.
Mark Scheme for Question 1
(a) 1 mark: Use of the correct equation v = fλ.
1 mark: Correct answer: f = v / λ = 2.0 / 0.50 = 4.0 Hz.
(b) 1 mark: Amplitude is the maximum displacement of a point on the wave from its equilibrium position.
Question 2 (5 marks)
Figure 1 shows two points, A and B, on a progressive transverse wave. The distance between A and B is 1.5 m. The wave travels with a speed of 6.0 m s⁻¹, and the time for point A to complete one oscillation is 0.50 s.
(a) Calculate the wavelength and frequency of the wave.
(b) State the phase difference between points A and B.
(c) Describe how displacement, wavelength, frequency, and wave speed are related in a progressive wave.
Mark Scheme for Question 2
(a)
1 mark: Period T = 0.50 s, frequency f = 1 / T = 2.0 Hz.
1 mark: Use of v = fλ → λ = v / f = 6.0 / 2.0 = 3.0 m.
(b)
1 mark: Phase difference = (distance / wavelength) × 360° = (1.5 / 3.0) × 360° = 180° (π radians).
(c)
1 mark: Displacement describes how far a point is from equilibrium at a given time.
1 mark: Wavelength is the distance between successive points in phase (e.g. crest to crest).
1 mark: Frequency is the number of oscillations per second, related to period by f = 1 / T.
1 mark: Wave speed is given by v = fλ, showing how frequency and wavelength determine the rate of wave propagation.

