OCR Specification focus:
‘Determine specific latent heat of fusion and vaporisation using electrical heating experiments.’
In thermal physics, the measurement of latent heat through electrical methods allows precise determination of the energy required for phase changes. These experiments connect electrical energy input to thermal energy transfer, demonstrating energy conservation and the physical principles of melting and boiling.
Measuring Latent Heat Electrically
Understanding Latent Heat
Latent heat refers to the energy absorbed or released during a change of state without a change in temperature. When a solid melts or a liquid vaporises, the supplied energy alters the potential energy of particles rather than their kinetic energy, maintaining a constant temperature.
Specific latent heat (L): The energy required to change the state of 1 kg of a substance without a change in temperature.
Latent heat is distinct from specific heat capacity, which relates to temperature change within a single phase. During a phase change, temperature remains constant even though internal energy increases.
Electrical Method: Overview
Electrical methods are ideal for accurately determining specific latent heats of fusion and vaporisation because they provide a known, measurable energy input via an electrical heater. By relating the electrical energy supplied to the mass of the substance that changes state, one can calculate latent heat precisely.
EQUATION
—-----------------------------------------------------------------
Energy for phase change (E) = m L
E = Electrical energy supplied = V I t
m = Mass of substance changed (kg)
L = Specific latent heat (J kg⁻¹)
V = Potential difference (V)
I = Current (A)
t = Time for heating (s)
—-----------------------------------------------------------------
The combination of these relationships allows the specific latent heat to be determined from measurable quantities:
L = (V I t) / m
Measuring the Specific Latent Heat of Fusion
Principle
To measure the specific latent heat of fusion, energy is supplied to a solid at its melting point (commonly ice) until it becomes liquid. The key is ensuring the temperature remains constant throughout the melting process.
Apparatus
Electrical heater (resistance coil)
Power supply with voltmeter and ammeter
Thermally insulated container (e.g. a beaker or calorimeter)
Balance for accurate mass measurement
Ice or another suitable solid at melting temperature
Procedure
Set up the electrical circuit so that the heater is fully immersed in the solid at its melting point.
Record the potential difference (V), current (I), and time (t) of heating accurately.
Collect the melt produced due to the electrical heating and measure its mass (m) using a balance.
Ensure minimal heat loss by using insulation and preventing direct heat transfer to the surroundings.
Calculate the specific latent heat of fusion using L = (V I t) / m.
Sources of Error
Heat absorbed by the container or lost to the environment.
Incomplete melting before recording measurements.
Residual water on the surface of the solid altering mass readings.
To improve accuracy, perform the experiment in a draught-free environment, use dry ice, and ensure the heater and container are pre-cooled to near melting temperature before measurement begins.
Measuring the Specific Latent Heat of Vaporisation
Principle
The specific latent heat of vaporisation is measured by supplying electrical energy to a liquid at its boiling point and determining the energy required for it to vaporise. Water is commonly used due to its well-known properties and ease of handling.
Apparatus
Electrical heater or immersion heater
Power supply with voltmeter and ammeter
Condenser or steam collection system
Balance for mass loss measurement
Insulated container to minimise heat losses
Procedure
Heat the liquid with a known potential difference and current until it boils steadily.
Record the steady readings of V, I, and t for a controlled heating interval.
Measure the mass of liquid vaporised (m) during this period using either a mass loss method or by collecting the condensate.
Apply the relationship L = (V I t) / m to find the specific latent heat of vaporisation.
Important Considerations
Maintain a steady rate of boiling to ensure constant temperature.
Ensure no vapour escapes unmeasured.
Use a lagged container to reduce heat transfer to the surroundings.
Correct for energy lost by the apparatus by conducting a control experiment with no phase change occurring.
Use a well-insulated calorimeter (Dewar flask) with a close-fitting lid to reduce thermal losses while the immersion heater operates.

Diagram of a calorimeter showing the insulated vessel used to limit heat exchange with the environment. This directly supports the requirement for good insulation when measuring latent heat electrically. This generic calorimeter diagram does not display the heater coil explicitly; it illustrates insulation and geometry only. Source.
Minimising Heat Losses and Experimental Errors
Accurate determination of latent heat depends heavily on thermal isolation and measurement precision.
Techniques for Improving Accuracy
Calorimeter design: Use polished, lagged, or vacuum-insulated containers to minimise heat loss.
Electrical measurements: Employ high-precision ammeters and voltmeters; ensure stable current throughout heating.
Timing: Use digital stopwatches to measure heating duration accurately.
Mass determination: Measure before and after heating using balances with sensitivity of at least 0.01 g.
Thermal equilibrium: Wait for the system to reach equilibrium before starting or ending timing.
Ensure the immersion heater is fully submerged and rated for the liquid used so that electrical power P = VI is transferred efficiently into the phase change.
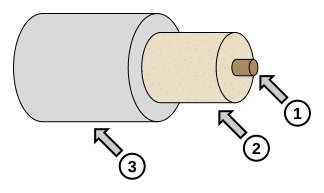
Annotated diagram of a tubular electric heater showing the resistance element (1), electrical insulator (2), and metal casing (3). This explains how the immersion heater converts electrical energy to thermal energy in the fluid. This is a generic heater diagram; it illustrates internal construction rather than the full calorimeter setup. Source.
Small systematic errors—such as unaccounted heat absorbed by the container or heat carried away by vapour—can significantly influence results. Repeated trials and control runs help identify and correct for these discrepancies.
Typical Results and Physical Interpretation
Values of specific latent heat of fusion for ice are typically around 3.34 × 10⁵ J kg⁻¹, while specific latent heat of vaporisation for water is about 2.26 × 10⁶ J kg⁻¹. These high values indicate that significant energy is required to break intermolecular bonds, especially during vaporisation when particles move far apart.
During both processes:
Temperature remains constant, confirming energy is used for changing potential energy, not kinetic energy.
The electrical method links microscopic energy transfer (particle-level) to macroscopic measurable quantities (voltage, current, time, and mass).
These experiments therefore illustrate the conservation of energy and the microscopic explanation of phase changes central to thermal physics.
FAQ
Electrical heating provides a precise and controllable energy input, since the electrical energy supplied can be directly calculated from measurable quantities — voltage, current, and time.
This allows accurate correlation between energy supplied and mass of substance changed, avoiding the uncertainties that come with methods like open-flame heating, which may lose energy through convection or radiation.
In addition, electrical methods make it easier to perform repeatable and safe measurements under controlled laboratory conditions.
The calculation assumes that:
The potential difference (V) and current (I) remain constant during heating.
All electrical energy supplied is transferred to the substance, not lost as heat to the surroundings.
The heater operates at 100% efficiency, meaning no internal energy is stored or dissipated within the heater itself.
In practice, some of these assumptions are not perfectly valid, so corrections or insulation improvements are used to minimise errors.
An immersion heater transfers energy directly into the substance, improving energy efficiency and reducing losses.
However, accuracy depends on:
The heater being fully submerged, preventing energy loss to air.
Good thermal contact between the heater and the liquid or solid phase.
Proper calibration to ensure voltage and current readings are accurate.
If part of the heater is exposed or if bubbles form on its surface during boiling, some electrical energy will not contribute to the phase change, lowering accuracy.
Heat losses to the surroundings cause underestimation of the actual energy transferred to the substance.
Using insulation, such as a Dewar flask or polystyrene lagging, ensures most of the supplied energy is used for melting or vaporisation rather than heating the air or the apparatus.
It also helps maintain thermal equilibrium, reducing unwanted cooling effects and stabilising the temperature at the phase change point.
Phase monitored: Fusion involves solid-to-liquid transitions; vaporisation involves liquid-to-gas.
Measurement method: Fusion experiments often collect meltwater, while vaporisation relies on measuring mass loss or condensate.
Temperature control: Fusion requires maintaining the solid at its melting point, whereas vaporisation needs a steady boiling point.
Heat losses: Vaporisation has greater losses due to escaping vapour and convection, making insulation more critical.
Both rely on E = VIt and E = mL, but the practical setups and dominant error sources differ significantly between the two.
Practice Questions
Question 1 (2 marks)
A student uses an electrical heater to determine the specific latent heat of fusion of ice.
Explain why the temperature of the ice remains constant while it melts, even though energy is being supplied by the heater.
Mark Scheme:
Energy supplied increases the potential energy of the particles (1)
Temperature (and thus average kinetic energy) remains constant during the change of state (1)
Question 2 (5 marks)
In an experiment to find the specific latent heat of vaporisation of water, a student uses an immersion heater connected to a 12 V supply drawing a current of 3.0 A. The heater operates for 4.0 minutes, and during this time 9.0 g of water is converted to steam at 100 °C.
(a) State an appropriate equation to calculate the specific latent heat of vaporisation of water. (1 mark)
(b) Calculate the specific latent heat of vaporisation of water using the data provided. (3 marks)
(c) Suggest one reason why the value obtained may be lower than the accepted value and explain how the experimental procedure could be improved. (1 mark)
Mark Scheme:
(a) E = mL or L = E / m (1)
(b)
Substitute electrical energy: E = V I t = 12 × 3.0 × (4.0 × 60) = 8640 J (1)
Convert mass to kg: m = 9.0 g = 0.0090 kg (1)
Calculate L: L = 8640 / 0.0090 = 9.6 × 10⁵ J kg⁻¹ (1)
(c)
Some heat is lost to the surroundings or used to heat the container rather than the water (1)
Improvement: Use a lagged/insulated container or perform a control run to correct for heat loss (1)

