OCR Specification focus:
‘Centripetal force is F = mv²/r or F = mω²r acting towards the centre.’
Centripetal force maintains an object’s circular motion by continually pulling it towards the circle’s centre, changing its direction while keeping speed constant in uniform circular motion.
Understanding Centripetal Force
When an object moves in a circle at constant speed, it is said to undergo uniform circular motion. Although its speed remains constant, its velocity continually changes because direction changes continuously. This change in velocity implies the presence of acceleration — specifically, centripetal acceleration, directed towards the centre of the circle. Consequently, a centripetal force must act to produce this acceleration.
The Nature of Centripetal Force
The term centripetal means ‘centre-seeking’. It refers to the direction of the force necessary to keep an object moving in a circular path. Without this inward force, the object would move in a straight line, as dictated by Newton’s first law of motion. Therefore, centripetal force is not a new type of force, but rather the resultant (net) force that acts towards the centre of the circle.
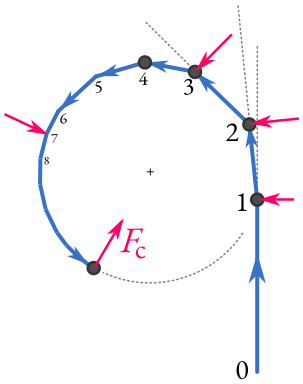
A particle’s path bends into a circle under a continuously acting inward force. This visual emphasises that “centripetal force” describes the net inward effect, aligning with F = mv²/r = mω²r when motion is uniform. Extra detail: the stepped “kick” construction is a pedagogical device to show the limit to continuous force. Source.
Centripetal Force: The net force that acts on an object moving in a circular path, directed towards the centre, maintaining the object’s circular motion.
Mathematical Expressions for Centripetal Force
Centripetal force can be expressed using two equivalent equations depending on whether the motion is described in terms of linear velocity (v) or angular velocity (ω).
EQUATION
—-----------------------------------------------------------------
Centripetal Force (F) = mv²/r
F = magnitude of the centripetal force (newtons, N)
m = mass of the object (kilograms, kg)
v = linear (tangential) velocity (metres per second, m s⁻¹)
r = radius of the circular path (metres, m)
—-----------------------------------------------------------------
This equation arises from Newton’s second law, where the net force equals mass times acceleration (F = ma). In circular motion, the acceleration is centripetal acceleration (a = v²/r), hence F = mv²/r.
The same relationship can be expressed in terms of angular velocity, using the link v = ωr.
EQUATION
—-----------------------------------------------------------------
Centripetal Force (F) = mω²r
F = magnitude of the centripetal force (newtons, N)
m = mass of the object (kilograms, kg)
ω = angular velocity (radians per second, rad s⁻¹)
r = radius of the circular path (metres, m)
—-----------------------------------------------------------------
Both forms describe the same physical situation. The choice between them depends on whether information about angular or linear quantities is available.
Direction and Characteristics of Centripetal Force
Centripetal force always acts perpendicular to the object’s velocity vector at every instant. This perpendicular nature ensures that the speed remains constant, as the force changes the direction of motion but not its magnitude. The velocity continuously rotates, maintaining the object’s circular trajectory.
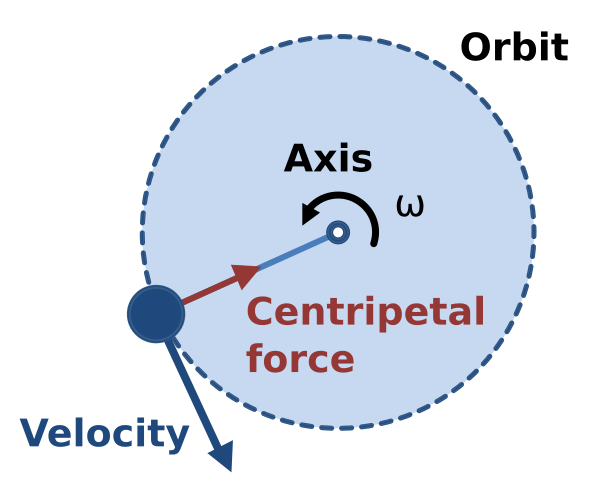
A particle in uniform circular motion with tangential velocity v and centripetal force Fc directed towards the centre. The force is perpendicular to velocity, changing direction but not speed. Labels are minimal and align with A-level expectations. Source.
Key points to note:
The direction of centripetal force is towards the centre of the circle.
The direction of the object’s velocity is tangential to the circle.
Since force and velocity are perpendicular, no work is done by the centripetal force (the object’s kinetic energy remains constant).
If the centripetal force were removed, the object would move tangentially, leaving the circular path.
Common Sources of Centripetal Force
Depending on the physical situation, various forces can provide the necessary centripetal component. In all cases, the resultant inward force equals mv²/r.
Typical examples include:
Tension in a string for an object being whirled in a horizontal or vertical circle.
Gravitational force providing the centripetal pull for planets orbiting the Sun.
Frictional force between tyres and road for a car turning around a bend.
Normal reaction between a vehicle and a banked track.
Electrostatic or magnetic forces for charged particles moving in circular paths in fields.
In each case, the same fundamental principle applies — the net inward force maintains circular motion by continuously changing the direction of velocity.
Dependence of Centripetal Force on Motion Parameters
Centripetal force depends strongly on speed, radius, and mass:
It is proportional to mass (m) — heavier objects require more force to follow the same circular path.
It is proportional to the square of velocity (v²) — doubling the speed quadruples the required centripetal force.
It is inversely proportional to radius (r) — smaller circles demand greater inward force.
These dependencies explain why vehicles must slow down when turning sharply and why satellites in lower orbits need greater centripetal forces than those further out.
Relationship to Centripetal Acceleration
Centripetal force and centripetal acceleration (a = v²/r) are directly linked through Newton’s second law. While acceleration describes the rate of change of velocity direction, the force represents the cause of that acceleration. Both quantities share the same direction — always towards the centre.
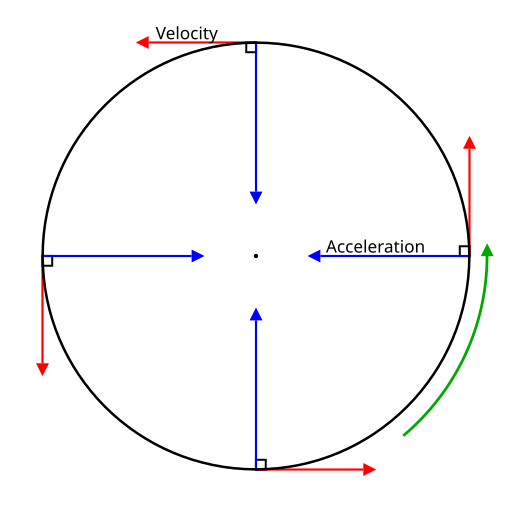
Uniform circular motion with tangential velocity and centripetal acceleration vectors. The acceleration points to the centre at every instant, establishing F = ma₍c₎ and hence the centripetal force expressions. Labels are concise and focused on vectors only. Source.
A crucial insight is that centripetal acceleration does not arise from a change in speed, but from the continual change in direction of the velocity vector.
Distinguishing Centripetal and Centrifugal Effects
Students often confuse centripetal force with the so-called centrifugal force. In reality, centrifugal force is not a real force but a fictitious or apparent force experienced in a rotating reference frame. It appears to act outward because the observer is rotating with the system. From an inertial frame, only the inward centripetal force truly acts on the object.
Understanding this distinction helps avoid misconceptions when analysing circular motion problems, particularly in rotating systems or vehicles negotiating curves.
Practical Implications and Conceptual Understanding
Centripetal force underpins many real-world applications and engineering designs:
Safety in road design: Roads are banked to reduce reliance on friction alone for providing the necessary centripetal force.
Rotational machinery: Rotors and turbines rely on material strength to withstand large centripetal forces at high angular speeds.
Satellites and planetary motion: Gravitational force acts as the centripetal pull keeping celestial bodies in stable orbits.
Laboratory experiments: In setups such as the whirling bung investigation, tension in the string provides measurable evidence for the relationship F = mv²/r.
Through these varied contexts, the formulae F = mv²/r and F = mω²r remain foundational to understanding the physics of rotational systems.
FAQ
Work is done only when a force has a component in the direction of displacement. In uniform circular motion, the centripetal force is always perpendicular to the object’s instantaneous velocity.
This means there is no component of force in the direction of motion, so no work is done.
The kinetic energy and speed remain constant because the force merely changes the direction of the velocity, not its magnitude.
No — the magnitude and direction of the centripetal force must be correctly balanced to maintain uniform circular motion.
If the force magnitude varies, the speed of the object will change.
If the direction of the net force shifts away from the centre, the motion will no longer be perfectly circular, becoming elliptical or irregular instead.
Thus, maintaining a constant inward net force is essential for true uniform circular motion.
For an object whirled in a circle by a string, tension provides the centripetal force.
When the motion is horizontal, tension acts entirely towards the centre.
In vertical circles, tension varies with position because weight also acts on the object.
At the top of the circle, tension and weight both act towards the centre.
At the bottom, tension acts towards the centre but weight acts outward relative to it, requiring greater tension to maintain the circular path.
Centripetal force is given by F = mω²r. The force depends on the square of the angular velocity.
Doubling the angular velocity increases the required centripetal force by a factor of four.
This occurs because faster rotation means the direction of velocity must change more rapidly, producing a larger centripetal acceleration (a = ω²r) that the force must supply.
No. Centripetal force is not a new kind of force; it is the name given to the resultant inward force that causes circular motion.
Depending on the context, it may be provided by:
Tension in a string,
Gravitational attraction,
Friction, or
Electrostatic/magnetic forces.
The term simply describes the role of the force — pulling the object towards the centre — rather than identifying a separate physical interaction.
Practice Questions
Question 1 (2 marks)
An object of mass 0.5 kg moves in a horizontal circle of radius 0.8 m at a constant speed of 3.0 m s⁻¹.
(a) Calculate the centripetal force acting on the object.
(b) State the direction of this force.
Mark scheme:
(a)
• Use of F = mv²/r (1 mark)
• Substitution: F = (0.5 × 3.0²) / 0.8 = 5.625 N, correctly rounded to 5.6 N (1 mark)
(b)
• Force directed towards the centre of the circular path (1 mark)
(Maximum 2 marks)
Question 2 (5 marks)
A small ball of mass 0.2 kg is attached to a light string and whirled in a horizontal circle at constant speed.
The radius of the circle is 0.6 m, and the tension in the string is measured to be 8.0 N.
(a) Derive an expression for the speed of the ball in terms of the given quantities.
(b) Calculate the angular velocity of the ball.
(c) Explain why the ball moves in a circular path rather than a straight line, referring to the direction of the net force and velocity.
Mark scheme:
(a)
• Start with F = mv²/r (1 mark)
• Rearrange to give v = √(Fr/m) (1 mark)
(b)
• Substitution: v = √(8.0 × 0.6 / 0.2) = √24 = 4.9 m s⁻¹ (1 mark)
• Use ω = v / r = 4.9 / 0.6 = 8.2 rad s⁻¹ (1 mark)
(c)
• The force (tension) acts towards the centre of the circle (1 mark)
• The velocity of the ball is tangential to the circle, so the perpendicular inward force changes its direction but not its speed (1 mark)

