OCR Specification focus:
‘Use a whirling bung setup to investigate circular motion and verify centripetal relationships.’
The whirling bung investigation is a classic physics experiment used to demonstrate uniform circular motion, allowing students to verify theoretical relationships between centripetal force, mass, velocity, and radius.
Understanding the Whirling Bung Setup
The whirling bung experiment involves rotating a rubber bung in a horizontal circle by means of a string threaded through a glass tube, with a weight hanging vertically below. The hanging weight provides the centripetal force required to maintain circular motion. This simple yet powerful setup allows for a direct investigation into the fundamental relationships governing centripetal acceleration and force.
The apparatus usually consists of:
A rubber bung (mass m) attached to one end of a string.
A glass or plastic tube through which the string passes, serving as a handle.
Hanging masses (providing tension) attached to the other end of the string.
A marker on the string to measure the radius of rotation.
Students spin the bung so it moves in a horizontal circular path at constant speed, while the tension in the string balances the weight of the hanging mass.
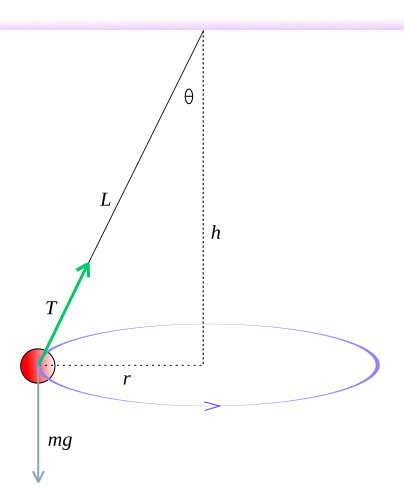
Diagram of a conical pendulum showing the string angle and tension components. The horizontal component provides the centripetal force, while the vertical component balances weight. Angle labels slightly exceed syllabus detail but clarify how tension resolves to give F=mv2/rF = mv^2/rF=mv2/r. Source.
Forces Acting on the Bung
The whirling bung experiences a tension force directed along the string towards the centre of the circular path.
Vector diagram for uniform circular motion with tangential velocity and inward centripetal force marked. It reinforces that only the inward component changes direction of motion. Minor extra labels may appear but remain within conceptual scope. Source.
This inward force provides the centripetal force necessary for circular motion. The weight of the bung acts vertically downward, but because the motion is horizontal, it is the tension that governs the circular path.
Centripetal Force: The net force directed towards the centre of a circular path that keeps an object moving in circular motion.
If the tension is not correctly matched to the centripetal requirement, the motion will not be stable — the bung will either rise or fall, disrupting uniform motion.
Relationship Between Centripetal Force, Speed, and Radius
The theoretical relationship between the quantities in circular motion can be expressed mathematically.
EQUATION
—-----------------------------------------------------------------
Centripetal Force (F) = m v² / r
F = Centripetal force (N)
m = Mass of the object (kg)
v = Tangential speed of the object (m s⁻¹)
r = Radius of the circular path (m)
—-----------------------------------------------------------------
This relationship indicates that the centripetal force increases with the square of the velocity and decreases with increasing radius. Hence, maintaining a constant radius and varying the speed enables the verification of this proportional relationship experimentally.
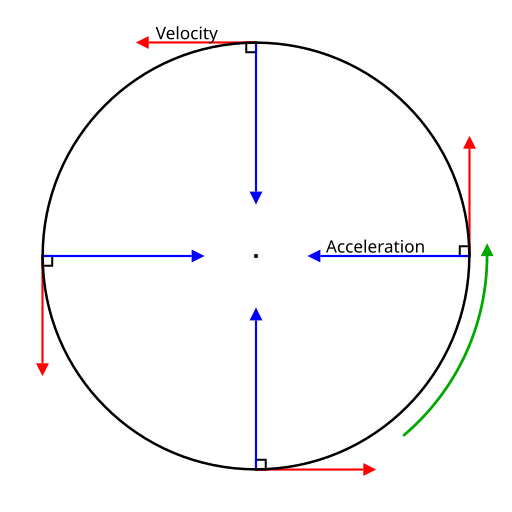
Diagram showing velocity vectors tangent to the circle and acceleration vectors directed to the centre. It visually links a=v2/ra = v^{2}/ra=v2/r to inward acceleration consistent with tension providing centripetal force. No extraneous information beyond syllabus level. Source.
Between the tension in the string and the gravitational force on the hanging mass, equilibrium occurs when:
T = mₕ g = m_b v² / r,
where mₕ is the hanging mass and m_b is the mass of the bung.
Experimental Method
The method for the whirling bung investigation is systematic and designed to reduce uncertainty.
Step 1 – Setting up the apparatus
Attach a rubber bung to one end of a strong, lightweight string.
Pass the string through a hollow glass tube to act as a handle and allow smooth rotation.
Tie a small weight or mass hanger at the lower end of the string to provide tension.
Mark a reference point on the string above the tube to set a fixed radius of rotation.
Step 2 – Initiating circular motion
Hold the tube vertically and rotate the bung in a horizontal circle.
Adjust the speed until the marker remains at a constant position above the tube — this ensures that the tension equals the weight of the hanging mass.
The hanging mass should remain stationary in the vertical direction, confirming equilibrium.
Step 3 – Recording data
Measure:
Time period (T) for a given number of revolutions using a stopwatch.
Radius (r) from the centre of the circle to the point of rotation.
Masses of both the bung and hanging weight using a balance.
The speed (v) can be determined from the radius and time period using the relationship:
EQUATION
—-----------------------------------------------------------------
Tangential Speed (v) = 2πr / T
v = Tangential speed (m s⁻¹)
r = Radius of circular motion (m)
T = Time period for one revolution (s)
—-----------------------------------------------------------------
This allows the calculation of centripetal force using the earlier equation.
Step 4 – Repeating and varying variables
To verify the centripetal relationships, students can:
Keep the radius constant and vary the mass or speed of the bung.
Record multiple trials to ensure consistency.
Plot graphs such as F vs v² or F vs 1/r, expecting linear relationships.
Analysis and Verification
The experimental data can be used to test the predicted proportionalities from theory:
At constant r and m, F ∝ v².
At constant v, F ∝ 1/r.
These trends confirm that the tension in the string provides the centripetal force necessary for circular motion.
Students can compare experimental slopes of their graphs with theoretical values calculated using known masses and gravitational acceleration (g = 9.81 m s⁻²). Agreement within uncertainties validates the theoretical model.
Accuracy and Precautions
Precision and safety are key when conducting the experiment.
Accuracy considerations
Ensure the radius remains constant by maintaining the position of the marker.
Measure the time for multiple revolutions to reduce timing error.
Use small angular displacements to minimise vertical movement of the bung.
Repeat measurements for reliability and average results to smooth random errors.
Safety considerations
Conduct the experiment in a clear area to prevent injury from the rotating bung.
Use a strong, secure string to prevent snapping at high speeds.
Wear safety goggles and ensure the tube is handled carefully.
Educational Value
This investigation provides hands-on reinforcement of abstract physics principles. By directly manipulating radius, mass, and speed, students gain a concrete understanding of how centripetal acceleration depends on these variables. The whirling bung experiment elegantly connects Newton’s laws of motion with circular dynamics, offering an essential bridge between theoretical and practical physics at the A-Level standard.
FAQ
Keeping the radius constant ensures that only one variable—typically the speed of the bung—changes during data collection. This isolates the effect of speed on centripetal force, allowing students to verify the relationship F ∝ v² accurately.
If the radius varies even slightly, the tension and angular velocity also change, leading to inconsistent data. Marking a fixed point on the string above the tube helps maintain a constant radius throughout the experiment.
Timing individual revolutions introduces large random errors. To reduce these:
Time multiple revolutions (e.g. 10–20) and divide by the number of revolutions to find the average period.
Use electronic timing gates or a high-speed camera if available.
Have two observers—one timing, one counting revolutions—to reduce human reaction errors.
These refinements improve precision and help produce a more reliable verification of centripetal relationships.
If rotated too slowly, the tension in the string is less than the weight of the hanging mass, causing the mass to fall and the radius to shorten.
If rotated too quickly, the tension exceeds the weight, pulling the hanging mass upward and increasing the radius.
Only when the rotation speed is just right does the system reach equilibrium—when the marker stays at a fixed height and the mass remains stationary.
In the whirling bung setup, the speed of the bung remains constant, and the force is always perpendicular to the velocity, changing only its direction.
In contrast, simple harmonic motion involves oscillations with a restoring force that changes direction along one axis.
The bung’s motion has constant angular speed and centripetal acceleration, which are key features of uniform circular motion, not oscillatory motion.
Direct measurement can be achieved using a force sensor or newton meter in place of the hanging mass.
The bung is rotated horizontally while the sensor records real-time tension.
This method allows investigation of instantaneous changes in force if speed or radius vary.
However, it requires careful calibration to ensure the sensor’s mass and friction do not affect the motion, making the traditional hanging mass method simpler for classroom verification.
Practice Questions
Question 1 (2 marks)
In the whirling bung experiment, a rubber bung is swung in a horizontal circle on the end of a string.
State the direction of the resultant force on the bung and name the physical quantity that provides this force.
Mark Scheme:
1 mark for stating the resultant (net) force is directed towards the centre of the circular path.
1 mark for identifying the force as tension in the string.
Question 2 (5 marks)
In a whirling bung investigation, a rubber bung of mass 0.050 kg is rotated in a horizontal circle of radius 0.60 m.
A mass of 0.10 kg hangs vertically at the other end of the string, providing the tension required for circular motion.
The bung is rotated at a steady speed so that the hanging mass remains stationary.
(a) Explain why the hanging mass remains stationary when the bung is rotated at constant speed. (2 marks)
(b) Derive an expression for the speed of the bung in terms of the hanging mass (mh), the bung mass (mb), the radius (r), and g. (3 marks)
Mark Scheme:
(a)
1 mark for recognising that the tension in the string equals the weight of the hanging mass (T = mh g).
1 mark for noting that the vertical forces on the hanging mass are balanced, so it remains stationary.
(b)
1 mark for correctly stating the centripetal force on the bung: T = mb v² / r.
1 mark for equating the two expressions for tension: mh g = mb v² / r.
1 mark for rearranging to obtain v = √(mh g r / mb).

