OCR Specification focus:
‘Define magnetic flux density B; state the tesla as its SI unit.’
Magnetic flux density describes how strong and concentrated a magnetic field is, providing a quantitative measure essential for analysing electromagnetic interactions in many physical systems.
Magnetic Flux Density: Core Meaning and Importance
Magnetic flux density is a central quantity in electromagnetism because it links the strength of a magnetic field to the forces it produces on moving charges and currents. When studying magnetic behaviour in physical systems, students must be able to define this quantity accurately, express it using correct units, and understand the contexts in which it is used.
Magnetic Flux Density: The magnetic flux density (B) is the quantity that describes the strength and direction of a magnetic field, defined as the force per unit current per unit length on a conductor placed at right angles to the field.
This definition shows that magnetic flux density is not simply an abstract idea but a measurable and physically meaningful quantity that determines how strongly a magnetic field interacts with electric currents. Because it includes both magnitude and direction, it is classified as a vector quantity.
Units of Magnetic Flux Density
The OCR specification requires students to “state the tesla as its SI unit”, so a clear understanding of the tesla (T) is essential. The tesla is not merely a label; it corresponds directly to how much force a magnetic field exerts. One tesla represents a very strong magnetic field, much stronger than typical fields produced in everyday laboratory equipment.
Tesla: The tesla (T) is the SI unit of magnetic flux density. One tesla is the magnetic flux density that exerts a force of one newton on a one-metre length of wire carrying one ampere of current at right angles to the field.
This formal definition establishes a direct link between magnetic flux density and measurable physical quantities such as force, current, and length. It also helps students visualise the magnitude of a tesla in realistic physical situations. Although strong laboratory magnets may reach several tesla, the Earth’s magnetic field near the surface is only about 50 microtesla.
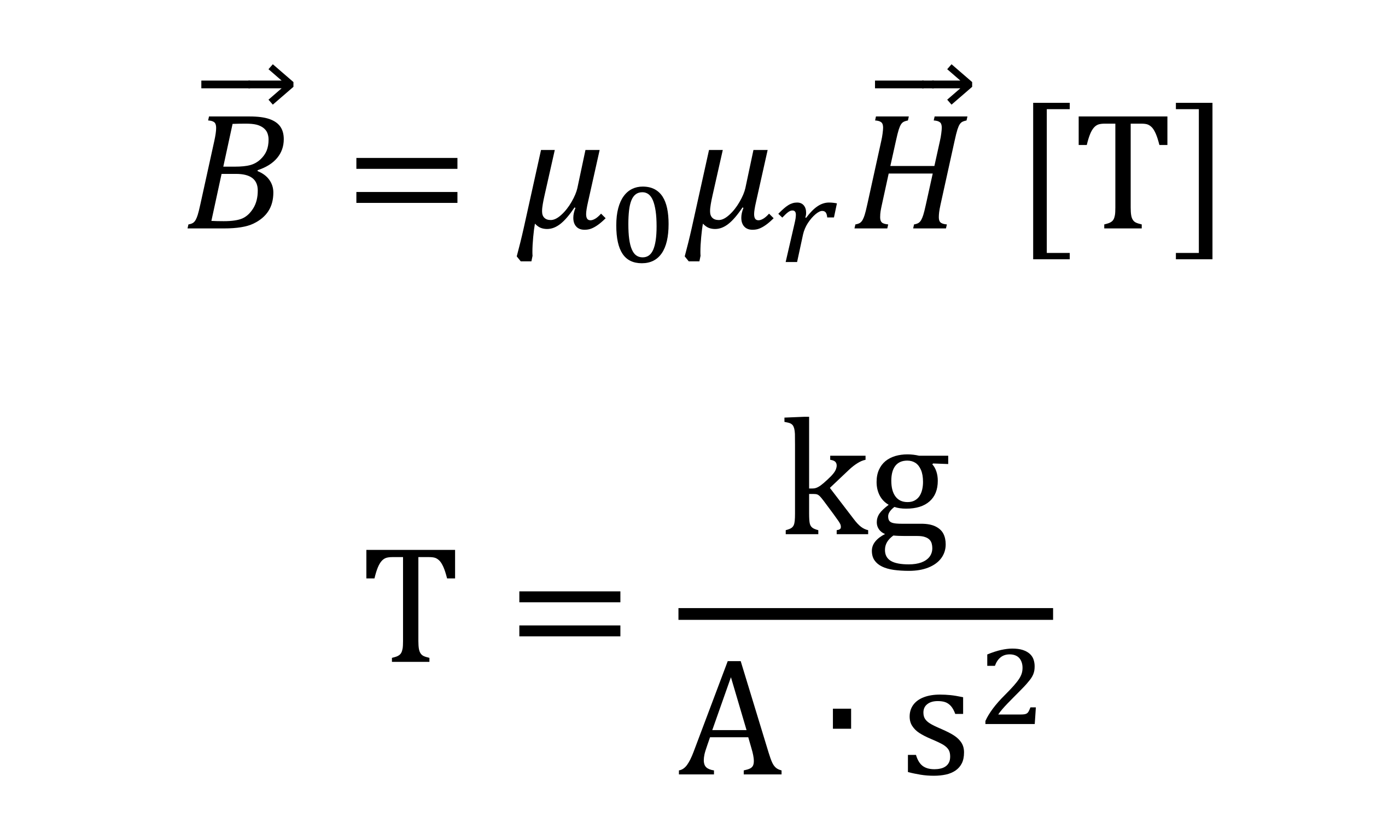
This diagram shows how magnetic flux density relates to magnetic field strength and permeability, and presents the tesla in SI base units, reinforcing its definition as a derived unit. Source.
In practice, magnetic flux density is often encountered in smaller units such as millitesla (mT) or microtesla (µT). Understanding the relationships among these units helps students interpret typical values found in laboratory and natural environments.
Vector Nature of Magnetic Flux Density
Because magnetic flux density is a vector quantity, it has both magnitude and direction. The direction of B is defined as the direction in which the north pole of a small test magnet would point if placed in the field. Direction is crucial when analysing magnetic interactions, particularly when using rules such as Fleming’s left-hand rule in later subtopics.
Key characteristics of the vector nature of B include:
Directionality: Magnetic effects depend on the orientation of B relative to currents or charges.
Right-hand grip rule: Although studied in another subsubtopic, it is important to note that B around a current-carrying wire forms concentric circles whose direction can be predicted using this rule.
Field representation: Magnetic flux density can be illustrated using magnetic field lines, where the density of the lines indicates the magnitude of B.
Understanding the vector nature of B allows accurate analysis of how magnetic fields influence physical systems.
Relationship Between Force and Magnetic Flux Density
Magnetic flux density plays a key role in determining the magnetic force experienced by a straight current-carrying conductor placed in a magnetic field. Although detailed force calculations belong to a later subsubtopic, it is appropriate here to show how B connects with measurable quantities.
EQUATION
—-----------------------------------------------------------------
Magnetic Force (on a current-carrying conductor) = B I L sinθ
B = Magnetic flux density in tesla (T)
I = Current in amperes (A)
L = Length of conductor in metres (m)
θ = Angle between B and the current direction in degrees or radians
—-----------------------------------------------------------------
The equation also demonstrates that magnetic flux density is most effective when the conductor is oriented at right angles to the field. When the conductor runs parallel to the magnetic field, the force becomes zero. This direction-dependence reinforces the idea that B describes not only magnitude but also directional influence.
Visual and Conceptual Representations of B
Magnetic flux density can be represented and interpreted in various ways, each contributing to a deeper understanding of magnetic behaviour.
Common representations include:
Field line diagrams showing the shape and strength of magnetic fields around magnets, wires, and solenoids.
Vector arrows indicating both magnitude and direction at specific points.
Mathematical relationships linking B to physical effects such as magnetic force or flux in induction scenarios.
Important conceptual points:
Stronger fields have denser field lines, indicating greater magnetic flux density.

This diagram shows the magnetic field of a bar magnet, with denser field lines near the poles representing greater magnetic flux density and weaker spacing farther away. Source.
Uniform fields (for example, between parallel pole pieces of a magnet) have straight, equally spaced field lines and a constant value of B.
Non-uniform fields vary in strength, meaning B changes with position.
Understanding these representations ensures that students can interpret magnetic fields in both qualitative and quantitative terms.
Practical Significance in Physics and Technology
Magnetic flux density is fundamental in the design and operation of many practical systems. While details of these devices lie beyond this subsubtopic, recognising the relevance of B enhances conceptual clarity.
Situations where magnetic flux density is essential:
Electromagnets used in lifting equipment or magnetic locks.
Motors and generators, where B influences torque or induced e.m.f.
Magnetic resonance imaging (MRI) machines, which rely on controlled strong magnetic fields.
Particle accelerators, where magnetic fields steer charged particles.
These applications demonstrate that magnetic flux density is not merely a theoretical construct but a vital parameter in modern technology.
FAQ
Magnetic flux density can be measured using a calibrated Hall probe, which produces a small voltage proportional to the magnetic field strength.
Hall probes are useful because they provide:
• Direct digital readings
• Accuracy even in non-uniform fields
• The ability to measure both the magnitude and direction of B
Their calibration must be checked regularly to ensure reliable values.
Magnetic flux density is defined through its effect on moving charges and currents, requiring both magnitude and direction.
Magnetic field strength H, although also a vector, is often used in material analysis where direction is secondary to examining how materials respond magnetically. This difference in context leads to B being emphasised as the primary physical field in many applications.
The maximum B depends on:
• The current supplied
• The number of turns in the coil
• The core material’s magnetic properties
Iron cores, for instance, increase B significantly due to their high permeability. However, saturation limits how much B can grow, even if current continues to increase.
The tesla is defined using relatively large base quantities such as one newton of force, one ampere of current, and one metre of wire, resulting in a large unit value.
Most natural and everyday magnetic fields—like the Earth’s field or small fridge magnets—produce relatively small forces on currents, which is why microtesla or millitesla values are more practical for everyday measurement.
Magnetic flux density decreases rapidly with distance from the magnet because the field spreads out into a larger area.
For a bar magnet:
• B is strongest at the poles where field lines are most concentrated
• The decrease with distance is non-linear
• The precise variation depends on magnet shape and internal magnetisation
This spatial variation is why field mapping produces curved, expanding field patterns around a magnet.
Practice Questions
Question 1 (2 marks)
State what is meant by magnetic flux density and identify its SI unit.
Question 1 (2 marks)
• Magnetic flux density is the force per unit current per unit length on a conductor placed at right angles to the magnetic field. (1)
• SI unit is the tesla (T). (1)
Question 2 (5 marks)
A straight wire of length 0.15 m carries a current of 4.0 A. The wire is placed in a uniform magnetic field of flux density B at right angles to the field lines.
(a) Write down the equation linking magnetic force, current, length of conductor, and magnetic flux density.
(b) The wire experiences a force of 0.30 N. Calculate the magnetic flux density.
(c) Explain why the force would be zero if the wire were aligned parallel to the magnetic field.
Question 2 (5 marks)
(a) Magnetic force = B I L sin(theta). (1)
(b) Rearranging to B = F / (I L). (1)
• Substitution: B = 0.30 / (4.0 × 0.15). (1)
• Correct final value: 0.50 T. (1)
(c) Explanation that sin(theta) = 0 when the conductor is parallel to the field, so the force becomes zero. (1)

