OCR Specification focus:
‘Recognise derived units built from base units, e.g. momentum kg m s–1; density kg m–3.’
Understanding derived units is essential in physics. They connect base quantities to more complex physical relationships, allowing consistent measurement, comparison, and verification of scientific equations and experimental data.
Derived Units and Their Importance
In physics, all measurable quantities are built upon a foundation of S.I. base units. However, most quantities encountered in the study of the physical world are derived quantities, which result from combining these base units through multiplication or division according to physical laws and definitions.
Derived units allow scientists and engineers to express a wide variety of phenomena consistently. For example, velocity, acceleration, force, momentum, energy, and pressure are all derived quantities. Their respective units are constructed from combinations of the seven S.I. base units: kilogram (kg), metre (m), second (s), ampere (A), kelvin (K), mole (mol), and candela (cd).
Understanding Derived Quantities
A derived quantity is obtained by combining one or more base quantities through a mathematical relationship defined by physical principles.
Derived Quantity: A physical quantity obtained by combining base quantities according to a physical law, expressed in terms of base units.
For instance, velocity is derived by dividing distance by time, while density results from dividing mass by volume. These derived relationships reflect how different physical properties interact.
Expressing Derived Units in S.I. Base Units
Every derived unit can be reduced to a combination of base units. This process allows verification of dimensional consistency and ensures that equations are homogeneous—that is, all terms within an equation have the same dimensional form.
EQUATION
—-----------------------------------------------------------------
Example: Velocity (v) = distance (s) / time (t)
v = s / t
s = distance in metres (m)
t = time in seconds (s)
Therefore, velocity unit = m s⁻¹
—-----------------------------------------------------------------
This breakdown is fundamental for both theoretical and experimental physics, as it allows one to identify and correct dimensional errors within physical equations or data analysis.
Common Derived Units
Momentum
Momentum is a measure of the motion of an object, defined as the product of mass and velocity.
EQUATION
—-----------------------------------------------------------------
Momentum (p) = mass (m) × velocity (v)
p = momentum, unit = kg m s⁻¹
m = mass, unit = kg
v = velocity, unit = m s⁻¹
—-----------------------------------------------------------------
Thus, the derived unit for momentum is kilogram metre per second (kg m s⁻¹).
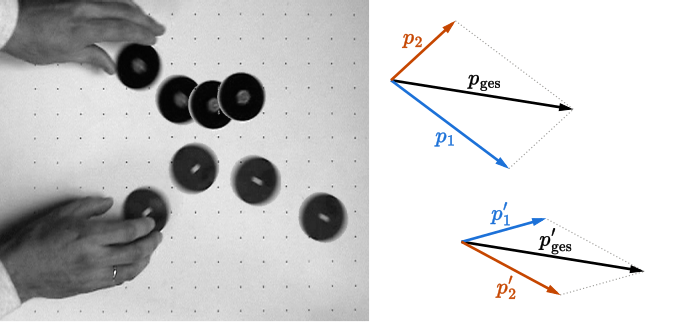
Vector diagram illustrating conservation of linear momentum in two dimensions for colliding pucks. Arrows depict initial and final momentum components and totals. While it does not label units, it directly visualises p = mv as a vector quantity. Source.
Density
Density quantifies how much mass is contained within a given volume.
EQUATION
—-----------------------------------------------------------------
Density (ρ) = mass (m) / volume (V)
ρ = density, unit = kg m⁻³
m = mass, unit = kg
V = volume, unit = m³
—-----------------------------------------------------------------
Therefore, the derived unit for density is kilogram per cubic metre (kg m⁻³).
A concise icon for the SI unit of density, kilogram per cubic metre (kg m⁻³). It highlights that density is mass per unit volume, aligning with ρ = m/V. The diagram is intentionally minimal, showing only the SI unit without extra context. Source.
Force
The concept of force arises from Newton’s second law of motion.
EQUATION
—-----------------------------------------------------------------
Force (F) = mass (m) × acceleration (a)
F = force, unit = N (newton) = kg m s⁻²
m = mass, unit = kg
a = acceleration, unit = m s⁻²
—-----------------------------------------------------------------
Hence, one newton (N) is equivalent to one kilogram metre per second squared (kg m s⁻²).
Relationships Among Derived Units
Many derived quantities build upon other derived quantities. For example:
Work (or energy) derives from force multiplied by distance, giving the unit joule (J) = N m = kg m² s⁻².
Power, the rate of doing work, is work divided by time, producing watt (W) = J s⁻¹ = kg m² s⁻³.
Pressure, defined as force per unit area, gives pascal (Pa) = N m⁻² = kg m⁻¹ s⁻².
Charge, derived from current multiplied by time, yields the coulomb (C) = A s.
Potential difference, as energy per unit charge, gives volt (V) = J C⁻¹ = kg m² s⁻³ A⁻¹.
These examples demonstrate how new physical quantities can be expressed entirely in terms of the base S.I. units, ensuring internal consistency throughout scientific equations and experiments.
Derived Units in Dimensional Form
When expressing units, physicists often represent them in dimensional form using symbols that denote base quantities:
M for mass (kg)
L for length (m)
T for time (s)
I for electric current (A)
Θ for temperature (K)
N for amount of substance (mol)
J for luminous intensity (cd)
Examples of dimensional representations:
Velocity → [L T⁻¹]
Acceleration → [L T⁻²]
Force → [M L T⁻²]
Energy → [M L² T⁻²]
Power → [M L² T⁻³]
Pressure → [M L⁻¹ T⁻²]
This notation aids in dimensional analysis—a crucial tool for confirming whether equations are physically valid and homogeneous.
The Role of Derived Units in Practical Measurement
Derived units are not merely mathematical constructs; they have direct practical relevance in laboratory measurement, data analysis, and instrument calibration. For example:
When recording velocity, one ensures that both distance and time are measured in consistent S.I. units.
Measuring pressure involves understanding that instruments like manometers or barometers are effectively measuring a derived combination of mass, length, and time through force and area.
Engineers designing sensors, such as accelerometers or flow meters, depend on consistent derived unit relationships to calibrate devices accurately.
A misunderstanding of derived units can lead to significant experimental or design errors, such as inconsistent scaling, conversion mistakes, or physically impossible results.
Derived Units Beyond Mechanics
While mechanics provides the most intuitive examples, derived units extend across thermodynamics, electromagnetism, and atomic physics:
Specific heat capacity (c) = energy / (mass × temperature change) = J kg⁻¹ K⁻¹ = m² s⁻² K⁻¹
Electrical resistance (R) = potential difference / current = V A⁻¹ = kg m² s⁻³ A⁻²
Magnetic flux density (B) = force / (current × length) = N A⁻¹ m⁻¹ = kg s⁻² A⁻¹
Each derived unit builds upon the same logical structure of combining base units through fundamental relationships, ensuring that all physical quantities—no matter how abstract—can ultimately be traced back to the universal S.I. base system.
FAQ
Dimensional analysis ensures that all terms in an equation have the same dimensional form. This can reveal errors or confirm consistency.
To derive or verify an equation:
Write the dimensions of each physical quantity involved.
Combine them to match the dimensions of the required quantity.
If both sides of the equation have identical dimensions, the equation is dimensionally valid. However, this method cannot confirm numerical constants or dimensionless factors such as ½ or π.
Certain derived units represent quantities that occur frequently in physics, so they are assigned specific names and symbols for simplicity and clarity.
Examples include:
Newton (N) for force = kg m s⁻²
Joule (J) for energy = kg m² s⁻²
Pascal (Pa) for pressure = kg m⁻¹ s⁻²
This convention makes equations easier to read and communicate across scientific disciplines.
Yes. Some derived quantities are dimensionless because their base units cancel out completely.
Common examples include:
Refractive index (n) = speed of light in vacuum / speed of light in medium
Strain = change in length / original length
Relative density = density of a substance / density of water
Although these quantities have no physical dimension, they remain crucial in comparing physical properties and defining ratios.
Derived units ensure that all measurements are based on the same S.I. foundation. This allows scientists to:
Compare results from different experiments using the same units.
Combine equations from mechanics, thermodynamics, or electromagnetism without conversion errors.
Validate theoretical models by ensuring unit compatibility.
Without derived units linked to base quantities, scientific communication would become inconsistent and prone to significant systematic errors.
A derived unit with a special name (e.g. joule, newton, volt) is a convenient shorthand for complex base unit combinations.
A derived unit without a special name simply keeps its base-unit form, such as kg m⁻³ for density or m s⁻¹ for velocity.
While both types are equivalent in meaning and value, using named units improves readability in equations and makes physical relationships more intuitive for communication and problem-solving.
Practice Questions
Question 1 (2 marks)
State what is meant by a derived unit and give one example of a derived unit expressed in terms of S.I. base units.
Mark scheme:
1 mark for correctly stating that a derived unit is formed by combining base units according to a physical relationship or law.
1 mark for a correct example, e.g. newton (N) = kg m s⁻², or joule (J) = kg m² s⁻².
Question 2 (5 marks)
A student writes the following equation for energy:
E = F × t
where E is energy, F is force, and t is time.
(a) Using dimensional analysis, determine whether this equation is homogeneous.
(b) If it is not homogeneous, explain how the correct physical relationship should be written and justify your reasoning.
Mark scheme:
1 mark for identifying the dimensions of force: [M L T⁻²].
1 mark for determining that multiplying by time gives [M L T⁻¹].
1 mark for recognising that energy has dimensions [M L² T⁻²].
1 mark for correctly concluding that the equation is not homogeneous because [M L T⁻¹] ≠ [M L² T⁻²].
1 mark for stating that the correct relationship is E = F × d (distance), and explaining that energy is the product of force and displacement, not time.

