OCR Specification focus:
‘A physical quantity has a numerical value and a unit used to express it.’
All scientific measurements describe physical quantities, the foundation of physics understanding. These quantities express measurable aspects of nature using both a numerical value and a unit, enabling precise communication of results.
Understanding Physical Quantities
Physics seeks to describe the physical world quantitatively. Every measurable property — from the length of a rod to the current through a wire — is described as a physical quantity. Physical quantities provide meaning to experimental data and theoretical models, ensuring consistency across scientific disciplines.
Defining a Physical Quantity
Physical Quantity: A property of a material or system that can be measured and expressed as a numerical value multiplied by a unit.
Every physical quantity consists of two essential parts:
Numerical value – indicates how many times a chosen unit is contained within the measured quantity.
Unit – provides a standard of comparison for the measurement, ensuring universal understanding.
For example, saying the speed of an object is 5 m/s means its numerical value is 5 and its unit is metres per second (m/s).
The Role of Units
Units are the language of measurement in physics. They ensure that every result can be understood and compared globally. Without standardised units, measurements would lack coherence between scientists, experiments, and nations.
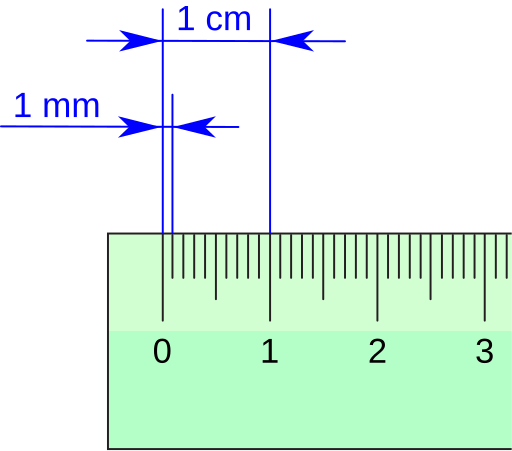
A clear vector illustration of a metric ruler showing centimetre numbers and millimetre ticks. It exemplifies how a chosen unit provides the scale to interpret a numerical value in practice. Source.
The International System of Units (S.I.) provides a universally accepted set of base and derived units. These are covered in later subsubtopics, but here, it is essential to understand that every physical quantity must be associated with an appropriate S.I. unit.
Categories of Physical Quantities
Physical quantities can be divided into two fundamental categories: base quantities and derived quantities. Understanding the distinction between these is vital for further study in physics.
Base Quantities
Base quantities are the fundamental building blocks from which all other measurements in physics are derived. Examples include:
Mass (kilogram, kg)
Length (metre, m)
Time (second, s)
Electric current (ampere, A)
Temperature (kelvin, K)
Amount of substance (mole, mol)
Each base quantity is independent and defined precisely by international agreement.
Derived Quantities
Derived quantities result from mathematical combinations of base quantities. These include:
Velocity (m/s) – derived from distance and time.
Force (N or kg·m/s²) – derived from mass, length, and time.
Density (kg/m³) – derived from mass and volume.
Derived quantities show how physical laws interconnect different measurable properties.
Numerical Value and Unit Relationship
Every measurement expresses how a physical quantity relates to a unit.
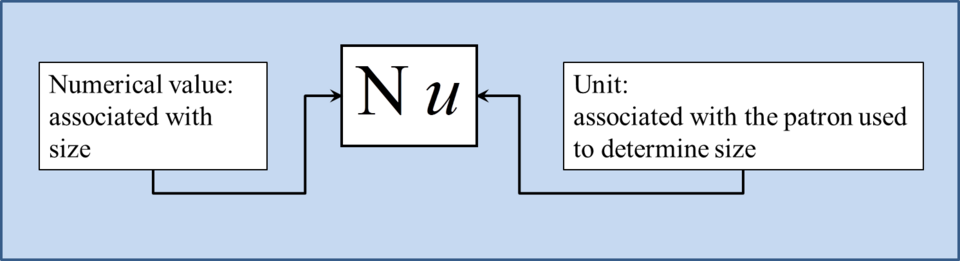
A concise schematic highlighting that the value of a dimensional quantity is the product of a numerical value and a unit. This clarifies why numbers alone are insufficient in physics and why units are essential for meaning. Source.
This can be represented as:
EQUATION
—-----------------------------------------------------------------
Physical Quantity (Q) = Numerical Value (n) × Unit (u)
Q = n × u
n = pure number (no unit)
u = standard measurement unit (S.I. or otherwise)
—-----------------------------------------------------------------
This relationship is fundamental in measurement. It enables scientists to convert between units, check the validity of equations, and ensure consistent results in experiments.
Example of Measurement Interpretation
If a time interval is recorded as 120 s, this means the physical quantity time has:
A numerical value: 120
A unit: seconds (s)
Changing the unit, for example to minutes, adjusts the numerical value but not the physical quantity itself. The time interval remains the same physical reality, only expressed differently.
The Need for Measurement Standards
In physics, measurement precision depends on consistency. Therefore, international bodies maintain standards for all base units. These standards are now defined using fundamental physical constants, such as:
The speed of light in a vacuum (c)
The Planck constant (h)
The elementary charge (e)
Such definitions ensure that physical quantities are independent of physical artefacts and can be replicated anywhere in the world.
Importance of Dimensional Consistency
Every physical quantity can be described by its dimension, showing how it relates to the base quantities. Dimensional analysis allows physicists to verify equations for homogeneity, ensuring that both sides of an equation describe quantities with identical dimensions. For instance, in the equation for speed:
EQUATION
—-----------------------------------------------------------------
Speed (v) = Distance (x) / Time (t)
v = speed, unit: m/s
x = distance, unit: m
t = time, unit: s
—-----------------------------------------------------------------
This equation is dimensionally consistent because both sides simplify to the base units of m·s⁻¹.
Measurable and Non-Measurable Properties
Only properties that can be measured and assigned numerical values with units qualify as physical quantities. Qualitative descriptions such as “hot”, “bright”, or “fast” become scientifically meaningful only when quantified:
Temperature: expressed in kelvin or degrees Celsius.
Brightness: expressed as luminous intensity in candela (cd).
Speed: expressed as metres per second (m/s).
Hence, quantification transforms observations into precise, comparable data suitable for analysis and theoretical modelling.
Representing Physical Quantities in Equations
Physical quantities in equations are typically represented by symbols with clearly defined meanings and units. When solving problems or deriving relationships:
Always specify the unit after numerical values.
Use consistent units throughout.
Avoid mixing unit systems (e.g., S.I. and imperial).
Inconsistent use of units is a common source of experimental and calculation errors.
Summary of Key Principles
To correctly identify and use physical quantities:
Each measurement must include both a numerical value and a unit.
Quantities without units are meaningless in scientific contexts.
The S.I. system provides a coherent framework for expressing all physical quantities.
Derived quantities are formed from combinations of base quantities.
Dimensional consistency is essential for verifying equations and ensuring physical correctness.
FAQ
In physics, only quantities that can be measured objectively allow for reproducible experiments and verifiable theories.
A measurable quantity provides:
A defined method of measurement, such as timing with a stopwatch or weighing with a balance.
A unit of comparison, ensuring results can be repeated and checked globally.
Unmeasurable or qualitative descriptions (like “hot” or “heavy”) lack precision and cannot be used in equations or data analysis, so they are excluded from scientific definition.
Yes. The same quantity can be expressed in different unit systems, provided conversions are accurate.
For example:
Speed can be given as m/s in S.I. units or km/h in non-S.I. terms.
Energy can be in joules (J) or kilowatt-hours (kWh).
However, OCR Physics always uses S.I. units for consistency in equations and exam answers. Non-S.I. units are acceptable only when clearly converted or contextualised.
A numerical value is a pure number showing how many times a unit fits into the measured quantity.
A measurement reading, on the other hand, includes both the number and the unit together (for example, 5 m or 20 s).
This distinction matters when converting between units — only the numerical value changes, while the physical quantity itself remains the same.
Prefixes like milli-, kilo-, and mega- scale physical quantities without altering their meaning.
For instance:
1 kilometre (km) = 1,000 metres (m)
1 millisecond (ms) = 0.001 seconds (s)
Although detailed study of prefixes appears later in the syllabus, understanding that prefixes simply adjust the size of the unit, not the quantity itself, supports clarity when interpreting or comparing measurements.
Global scientific collaboration relies on uniform definitions of quantities and units. The S.I. system ensures every experiment, calculation, and publication refers to the same standards.
Without agreed units:
Data comparison between countries or research institutions would be inconsistent.
Technological design and manufacturing could produce incompatible results.
Standardisation, maintained by the Bureau International des Poids et Mesures (BIPM), keeps physics universal and prevents ambiguity in communication and measurement.
Practice Questions
Question 1 (2 marks)
State what is meant by a physical quantity and give one example.
Mark Scheme for Question 1
1 mark: Correct definition — a property of a system or material that can be measured and expressed as a numerical value multiplied by a unit.
1 mark: Appropriate example — e.g. length, mass, time, temperature, electric current, or similar measurable quantity.
(Maximum 2 marks)
Question 2 (5 marks)
A student states that the speed of a car is 30 m/s.
(a) Identify the numerical value and the unit in this measurement. (2 marks)
(b) Explain why it is important that all physical quantities are expressed with both a numerical value and a unit. (2 marks)
(c) State whether speed is a base or derived quantity and justify your answer. (1 mark)
Mark Scheme for Question 2
(a)
1 mark: Numerical value identified as 30.
1 mark: Unit identified as metre per second (m/s).
(b)
1 mark: Explains that a unit provides a standard for comparison, allowing results to be universally understood.
1 mark: Explains that without a unit, a numerical value is meaningless because the scale of measurement is undefined.
(c)
1 mark: Correctly states that speed is a derived quantity, as it is obtained from base quantities (distance and time).

