OCR Specification focus:
‘Understand acceleration of free fall g and its approximate value near Earth’s surface in ideal conditions.’
Objects near Earth’s surface experience an acceleration due to gravity called free-fall acceleration (g), a constant defining how quickly objects accelerate when only gravity acts upon them.
The Concept of Free Fall
Free fall describes the motion of an object acted upon solely by the force of gravity, with air resistance neglected. When an object is in free fall, the only significant force influencing its motion is its weight, which arises from Earth’s gravitational attraction. This concept forms a cornerstone of classical mechanics and underpins later studies of projectile motion, energy transfer, and dynamics.
Free fall: The motion of an object under the influence of gravity alone, with negligible air resistance.
Every object in free fall experiences the same acceleration, regardless of its mass, provided that external forces such as drag are absent. This universality reflects a profound physical principle first recognised by Galileo Galilei, who demonstrated that in a vacuum, all objects fall with identical accelerations.
The Acceleration Due to Gravity (g)
The acceleration of free fall (g) represents the rate of change of velocity for an object falling freely towards Earth. It is a vector quantity, always directed towards the centre of the Earth.
Acceleration of free fall (g): The constant acceleration experienced by any object moving freely under the influence of Earth’s gravity alone.
EQUATION
—-----------------------------------------------------------------
Weight (W) = m × g
W = Weight (N)
m = Mass (kg)
g = Acceleration due to gravity (m s⁻²)
—-----------------------------------------------------------------
This equation expresses the relationship between an object’s mass and the gravitational force acting upon it. Here, weight is the gravitational force, while g is the proportionality constant connecting it to mass.
Between any two objects near Earth’s surface, the value of g remains approximately constant, though it can vary slightly with location.
The Approximate Value of g Near Earth’s Surface
The standard value of g used in A-Level Physics and most calculations is approximately 9.81 m s⁻². This value is determined experimentally and represents the average gravitational acceleration at sea level on Earth’s surface.
However, the precise value of g is not identical everywhere. Several environmental and planetary factors influence its magnitude, including:
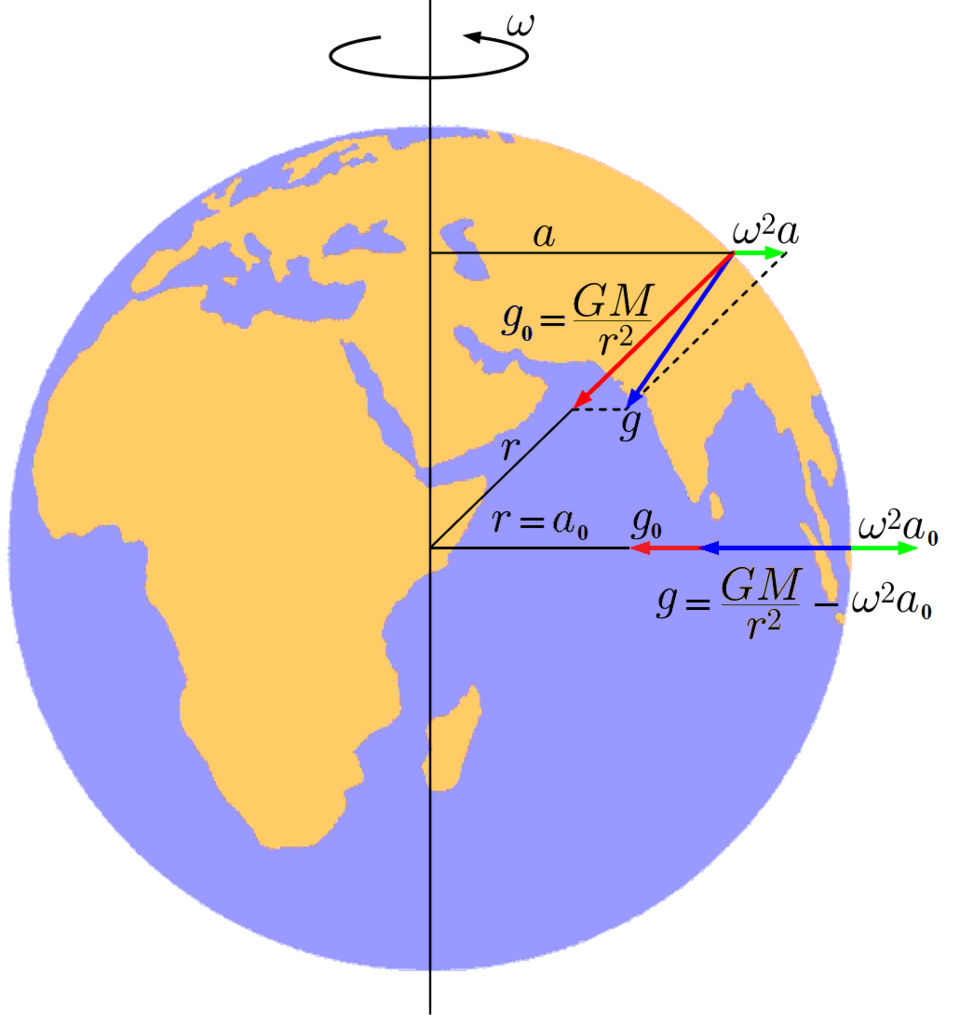
Vector diagram illustrating how gravitational attraction and the centrifugal effect from Earth’s rotation combine to give the effective acceleration due to gravity at the surface. This visual supports the small latitude-dependent variation (slightly lower at the equator, slightly higher at the poles). The diagram includes symbolic constants beyond OCR’s minimum, but they reinforce the definitions already given. Source.
Altitude: As height above the Earth’s surface increases, g decreases slightly, since gravitational force weakens with distance from Earth’s centre.
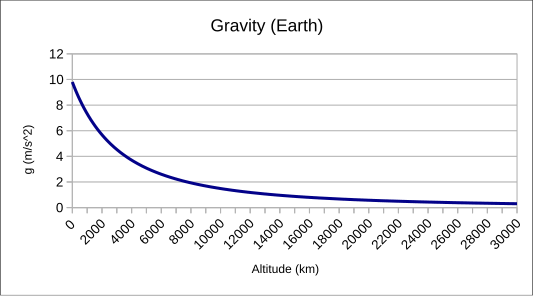
Graph of the acceleration due to gravity as a function of altitude above Earth’s surface, illustrating the inverse-square trend in a clean, uncluttered format. This directly supports the syllabus requirement to understand the concept and approximate value of g and its idealised variation with height. The horizontal axis extends to geostationary distances, which goes beyond typical A-Level contexts but does not add unnecessary complexity. Source.
Latitude: Because Earth rotates, points near the equator experience a centrifugal effect reducing effective g slightly, whereas at the poles this effect is absent, making g marginally greater.
Local density variations: Regional differences in rock density and mountainous terrain can alter the local gravitational field strength.
Typical values of g:
At the equator: approximately 9.78 m s⁻²
At the poles: approximately 9.83 m s⁻²
These differences, though small, can influence precision experiments and must be accounted for in gravitational field mapping or when performing high-accuracy measurements in laboratories.
Theoretical Basis of Gravitational Acceleration
The concept of free-fall acceleration arises directly from Newton’s Law of Universal Gravitation. According to this law, every mass attracts every other mass with a force proportional to their masses and inversely proportional to the square of the distance between their centres.
EQUATION
—-----------------------------------------------------------------
Gravitational Force (F) = G × (M × m) / r²
F = Gravitational force (N)
G = Gravitational constant (6.67 × 10⁻¹¹ N m² kg⁻²)
M = Mass of the Earth (5.97 × 10²⁴ kg)
m = Mass of object (kg)
r = Distance between object and Earth’s centre (m)
—-----------------------------------------------------------------
Combining this with Newton’s Second Law of Motion (F = ma) leads directly to an expression for g:
EQUATION
—-----------------------------------------------------------------
Acceleration due to gravity (g) = G × M / r²
G = Gravitational constant (6.67 × 10⁻¹¹ N m² kg⁻²)
M = Mass of the Earth (5.97 × 10²⁴ kg)
r = Mean radius of Earth (6.37 × 10⁶ m)
—-----------------------------------------------------------------
Substituting these values gives g ≈ 9.81 m s⁻², confirming the measured average. This derivation shows that g depends solely on universal constants and Earth’s mass and radius, reinforcing its predictable and consistent nature.
The Direction of g and the Vector Nature of Motion
The acceleration due to gravity acts vertically downwards towards the Earth’s centre. When analysing motion, g is treated as a constant vector pointing downward in diagrams and equations. Its direction determines how displacement, velocity, and acceleration are represented in vertical motion problems.
In free-fall motion:
Velocity increases linearly with time if upward resistance is neglected.
Displacement follows a quadratic relationship with time, showing that the distance fallen increases more rapidly the longer the object falls.
The object’s weight remains constant, but its kinetic energy increases due to continuous acceleration.
Ideal Conditions and Assumptions
For the concept of free-fall acceleration to apply accurately, several simplifying assumptions must be made:
Air resistance is negligible.
g is constant over the distance of the fall.
The object behaves as a point mass, ensuring rotational and shape effects are ignored.
The Earth’s surface is treated as flat over the region of motion.
These assumptions produce a mathematically ideal model enabling the use of SUVAT equations for uniformly accelerated motion. Real-world deviations—such as drag, buoyancy, and changing air density—introduce complexities, but these are treated in later topics.
Measuring and Using g in Practice
Although the numerical determination of g belongs to experimental work, its conceptual understanding is fundamental. Accurate awareness of g’s value allows prediction of how objects accelerate and provides a benchmark for comparing gravitational fields on other planets or moons. Engineers, physicists, and astronomers use this constant when analysing trajectories, designing safety systems, or modelling orbital mechanics.
The constancy and universality of g in idealised conditions make it one of the most important constants in physics, linking motion, forces, and gravitational interactions across multiple domains of study.
FAQ
Modern measurements of g use highly sensitive instruments such as gravimeters, which detect minute variations in the gravitational field.
There are two main types:
Absolute gravimeters, which measure the acceleration of a freely falling object in a vacuum using laser interferometry.
Relative gravimeters, which compare the strength of gravity at different locations using a calibrated spring-mass system.
These instruments can detect changes as small as one part in 10⁹, allowing scientists to map variations in g across the Earth’s surface accurately.
The value of g depends on two factors — the mass and radius of the celestial body.
EQUATION (conceptual reference only): g = GM / r²
A more massive planet produces a stronger gravitational field.
A larger radius reduces g because the gravitational force weakens with distance.
For example, Mars has g ≈ 3.7 m s⁻² (smaller mass and radius than Earth), while the Moon has g ≈ 1.6 m s⁻².
No. The value of g is a property of the Earth’s gravitational field and is unaffected by air resistance.
However, air resistance affects the motion of a falling object, causing it to accelerate less than g predicts. The measured acceleration (sometimes called the “effective acceleration”) will be smaller because the drag force opposes motion.
Removing air resistance, as in a vacuum chamber, reveals the true acceleration due to gravity, confirming that g is independent of the object’s shape or mass.
Earth’s rotation creates a centrifugal effect that slightly reduces the apparent value of g.
The effect is greatest at the equator, where rotational speed is highest, and least at the poles, where rotation has no lateral effect.
The centrifugal acceleration acts outward, opposing gravity and making g smaller by up to about 0.03 m s⁻² at the equator.
This is why precision measurements must account for latitude, especially in geophysical and engineering applications.
Yes, but only by an extremely small amount.
The Earth’s mass distribution changes slightly over time due to processes such as:
Tectonic activity, which shifts mass in the crust.
Melting of polar ice caps, which redistributes water mass.
Tidal forces from the Moon and Sun, which cause minor fluctuations.
These effects can alter g by a few millionths of a metre per second squared, measurable only with high-precision instruments. Over human timescales, g is effectively constant.
Practice Questions
Question 1 (2 marks)
State what is meant by free fall and give the approximate value of the acceleration due to gravity at the Earth’s surface.
Mark Scheme
1 mark: Correct definition — motion of an object under the influence of gravity alone, with air resistance neglected.
1 mark: Correct approximate value of acceleration due to gravity near Earth’s surface, 9.8 m s⁻² (accept 9.81 m s⁻² or 9.8 m/s²).
Question 2 (5 marks)
Explain why the acceleration due to gravity, g, is not exactly the same at all points on the Earth’s surface. In your answer, refer to at least two factors that cause these variations and describe how they affect the value of g.
Mark Scheme
1 mark: States that g varies because the Earth is not a perfect sphere or due to other physical factors (general statement of variation).
1 mark: Mentions altitude — g decreases slightly with increasing height above the Earth’s surface because the distance from the Earth’s centre increases.
1 mark: Mentions latitude — g is slightly lower at the equator and higher at the poles because of the Earth’s rotation causing a centrifugal effect.
1 mark: Describes the centrifugal effect correctly — this opposes gravity, reducing effective g near the equator.
1 mark: Mentions local variations in rock density or topography (mountains, geological structure) may also cause small changes in g.

