OCR Specification focus:
‘Use pressure = force ÷ area for solids, liquids and gases; apply to simple systems.’
Understanding Pressure
Pressure is a fundamental physical quantity describing how a force acts across a surface area. It plays a crucial role in understanding how solids support loads, how fluids exert forces on surfaces, and how gases act in enclosed spaces. A solid understanding of pressure allows physicists and engineers to analyse mechanical stability, fluid dynamics, and atmospheric effects with precision.
Pressure links force and area, demonstrating how the same force can produce vastly different effects depending on how it is distributed.
Defining Pressure
Pressure: The force per unit area acting normally (at right angles) to a surface.
Pressure quantifies the intensity of a force’s action over a surface. It is a scalar quantity, meaning it has magnitude but no direction. The SI unit of pressure is the pascal (Pa), where 1 Pa = 1 N m⁻².
The Pressure Equation
EQUATION
—-----------------------------------------------------------------
Pressure (p) = Force (F) ÷ Area (A)
p = F / A
p = pressure (Pa)
F = normal force (N)
A = area (m²)
—-----------------------------------------------------------------
This equation underpins all applications of pressure in solids, liquids, and gases. It highlights that for a given force, reducing the contact area increases pressure, and vice versa. This principle explains why sharp objects like knives or nails penetrate materials easily.
Pressure in Solids
In solids, forces are transmitted through rigid structures and concentrated at points or surfaces of contact. Pressure is determined by the perpendicular component of the force acting on the surface.
Key features:
Uniform pressure occurs when the force acts evenly over a surface.
Non-uniform pressure arises when forces vary across the surface, as in the case of uneven loads.
The normal contact force is the component of the force that acts perpendicular to the surface, responsible for generating measurable pressure.
Practical examples include:
A person standing on snow: using skis increases the contact area, reducing pressure and preventing sinking.
Structural engineering: ensuring materials can withstand the pressure exerted by loads without deformation.
In solids, the distribution of pressure often determines material choice and design — for instance, ensuring floor supports can manage high pressures under concentrated loads.
Pressure in Liquids
Liquids are incompressible fluids, meaning their volume does not change significantly under pressure. Pressure in a liquid acts equally in all directions at a given depth and increases with depth due to the weight of the fluid above.
Important characteristics:
Pressure acts perpendicular to any surface submerged in the liquid.
At a specific depth, pressure is the same regardless of the shape or orientation of the container.
Liquid pressure depends only on depth, density, and gravitational field strength, not on the total volume of liquid.
While this subsubtopic focuses on the general use of pressure = force ÷ area, it is crucial to recognise that in liquids, the source of the force often arises from the weight of the fluid column pressing on the area beneath it. Thus, even though liquids flow and conform to container shapes, the same pressure law applies to the surfaces they contact.
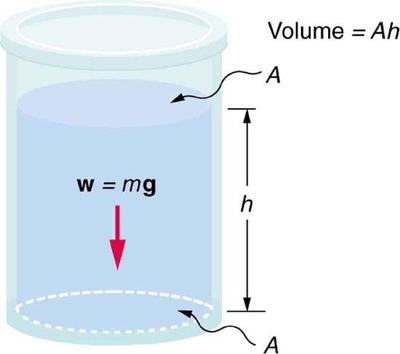
At a given level in a stationary liquid, the bottom surface supports the weight of fluid above, producing pressure on the area beneath. This simple diagram highlights force (weight) acting normally over area, consistent with p = F/A. Any indication of increasing pressure with depth is a natural consequence but not additional theory. Source.
Applications include:
Hydraulic systems, where pressure is transmitted uniformly to perform mechanical work.
Understanding buoyant forces and upthrust (developed in later subtopics).
Pressure in Gases
Gases differ from solids and liquids in that they are compressible and consist of particles moving freely and rapidly in all directions. Gas pressure originates from collisions of particles with the walls of their container.
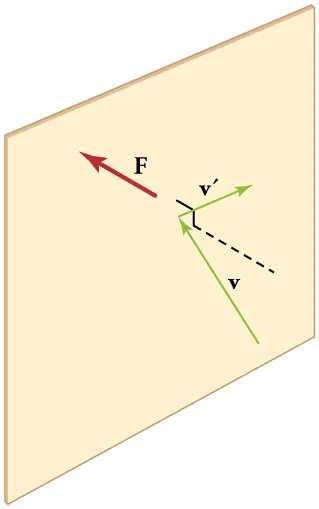
A gas exerts pressure when its molecules collide with the container walls, producing a net force per unit area. The diagram shows a molecule’s momentum component perpendicular to the wall reversing at impact, creating a force on the wall. This clean visual reinforces p = F/A for gases. Source.
Gas Pressure: The force per unit area exerted by gas molecules when they collide elastically with the surfaces of their container.
Gas pressure increases with temperature because faster-moving particles collide more frequently and with greater momentum. In an enclosed system, this microscopic behaviour produces a macroscopic pressure that can be measured and analysed using the same p = F/A relationship.
Key ideas:
Pressure acts uniformly in all directions within a gas.
If the container expands, the same force spreads over a larger area, reducing pressure.
Atmospheric pressure is the cumulative effect of air molecules colliding with the Earth’s surface.
Comparing Pressure in Solids, Liquids, and Gases
Although the same equation applies to all three states of matter, the origin of the force differs:
Solids: Pressure arises from mechanical contact forces applied externally or internally through stress.
Liquids: Pressure is caused by the weight of the liquid above a point, increasing with depth.
Gases: Pressure results from molecular motion and collisions within a confined volume.
This distinction is fundamental to understanding how pressure behaves in practical systems. For instance, a solid floor supports weight through compressive forces, water exerts pressure on submarine hulls due to fluid depth, and gases exert pressure in sealed containers through molecular impacts.
Measuring Pressure
Pressure can be measured using instruments suited to the state of matter involved:
Solids: Pressure sensors or force/area calculations.
Liquids: Manometers or pressure gauges connected at different depths.
Gases: Bourdon gauges or barometers for atmospheric pressure.

A Bourdon tube gauge converts applied pressure into pointer deflection, providing a direct reading of pressure in pascals or related units. Though it contains internal mechanics (curved tube and linkage), students only need to recognise it as a standard instrument for measuring pressure. Extra internal design details visible are beyond the syllabus requirement. Source.
Each device relies on the same physical principle of force distributed over area, calibrated to account for medium-specific properties such as density or compressibility.
Applications of Pressure Principles
Pressure concepts underpin numerous technologies and natural phenomena:
Hydraulic brakes and presses: Apply small forces over large areas to produce amplified output forces.
Atmospheric phenomena: Variations in air pressure create winds and weather patterns.
Medical devices: Syringes, blood pressure monitors, and respirators all rely on controlled pressure systems.
Engineering safety: Structural components and containment vessels are designed to withstand specific pressure limits.
These applications demonstrate how a single equation—p = F/A—extends across mechanical, fluid, and gaseous systems, illustrating the unifying nature of pressure in physics.
FAQ
Pressure and stress are closely related but not identical. Pressure refers to the normal force per unit area exerted by a fluid or solid in contact with a surface, acting equally in all directions.
Stress, however, is a measure of internal force distribution within a solid material and can act in different directions — tensile, compressive, or shear.
Pressure always acts perpendicularly and uniformly on a surface.
Stress can act parallel or perpendicular, depending on the type of deformation.
Pressure is a macroscopic quantity, while stress deals with microscopic internal forces within materials.
The sharpness of a knife affects the area of contact with the material. For the same applied force, a sharp knife has a smaller area, producing a larger pressure (p = F/A).
This higher pressure means that the material’s bonds are more easily broken or displaced, allowing the knife to cut effectively. A blunt knife spreads the same force over a larger area, reducing pressure and making cutting harder.
The principle illustrates how area reduction increases pressure without changing the applied force.
Liquids are incompressible and the particles can move freely, transmitting forces equally through all directions.
When an external force acts on a liquid, the molecules rearrange and transmit the force through collisions, distributing it uniformly.
This phenomenon follows Pascal’s principle, which states that pressure applied to an enclosed fluid is transmitted equally in all directions. It explains why a diver feels pressure from all sides and why hydraulic systems function effectively.
Increasing the temperature of a gas raises the average kinetic energy of its molecules. As a result:
Molecules move faster and collide with the container walls more frequently.
Each collision exerts a greater force on the walls.
Since pressure is the total force per unit area from these collisions, higher temperatures cause pressure to increase, provided the volume remains constant.
Conversely, cooling the gas reduces molecular motion and lowers the frequency and intensity of collisions, decreasing the pressure.
Although the wearer’s weight (force) is constant, the contact area between high heels and the ground is much smaller.
Using p = F/A:
Smaller A → larger p (pressure).
This results in a high pressure concentrated at the heel, which can dent flooring or sink into soft surfaces.
Flat shoes spread the same weight across a larger area, reducing pressure and preventing damage. This concept demonstrates how pressure depends on both force and area, not just on the weight applied.
Practice Questions
Question 1 (2 marks)
A student presses a metal block with a force of 30 N onto a table. The area of contact between the block and the table is 0.015 m².
(a) Calculate the pressure exerted by the block on the table.
(b) State the unit of pressure.
Mark scheme:
(a) Correct use of equation p = F / A (1 mark)
p = 30 / 0.015 = 2000 Pa or 2.0 × 10³ Pa (1 mark)
(b) Unit of pressure correctly stated as pascal (Pa) (1 mark)
Question 2 (5 marks)
Explain how the pressure exerted by a liquid changes with depth, and how this differs from the way pressure is exerted in a gas and in a solid. In your answer, refer to the source of the force responsible for the pressure in each case.
Mark scheme:
States that pressure in a liquid increases with depth (1 mark)
Explains that this increase is due to the weight of the liquid above (1 mark)
States that at a given depth, liquid pressure acts equally in all directions (1 mark)
States that in gases, pressure is due to collisions of moving molecules with the walls of a container (1 mark)
States that in solids, pressure results from normal contact forces distributed over the area of contact (1 mark)
Compares that in solids the pressure depends on applied external forces, in liquids it depends on depth, and in gases it depends on molecular motion (1 mark, awarded for clear comparison or synthesis)

