OCR Specification focus:
‘Explain upthrust on immersed objects; use Archimedes’ principle to solve buoyancy problems.’
Upthrust and Archimedes’ principle explain why objects float or sink in fluids. Understanding these forces is vital for analysing buoyancy, equilibrium, and practical applications in physics.
Upthrust and the Nature of Buoyancy
The Concept of Upthrust
When an object is immersed in a fluid, whether fully or partially, it experiences an upward force exerted by the fluid. This upward force is known as upthrust or buoyant force.
Upthrust: The upward force exerted by a fluid on an object wholly or partially immersed in it, opposing the weight of the object.
Upthrust arises because fluid pressure increases with depth. The pressure acting on the bottom surface of an immersed object is greater than that on the top surface, producing a resultant upward force.
This phenomenon explains why some objects float, others sink, and some remain suspended at a fixed level within a fluid. The magnitude of this upthrust is directly linked to the weight of the displaced fluid, as described by Archimedes’ principle.
Understanding Archimedes’ Principle
Statement of the Principle
Archimedes’ principle provides a quantitative link between the displaced fluid and the buoyant force experienced by the object.
Labeled diagram of Archimedes’ principle showing the buoyant force acting upward and weight acting downward on a partially immersed object. The fluid displaced by the object has a weight equal to the upthrust. This compact schematic matches the statement of the principle used in A-level questions. Source.
Archimedes’ Principle: The upthrust acting on a body immersed wholly or partially in a fluid is equal to the weight of the fluid displaced by the body.
This principle applies to both liquids and gases, though the effect is more noticeable in liquids due to their higher density. The principle allows physicists to predict whether an object will float, sink, or remain neutrally buoyant.
Deriving the Upthrust Mechanism
Pressure Variation with Depth
The force on any surface in a fluid depends on pressure and area. Since pressure increases with depth, the lower surface of an immersed body experiences a higher pressure than its upper surface.
EQUATION
—-----------------------------------------------------------------
Pressure–Depth Relation (p = ρgh)
p = ρgh
p = pressure (Pa)
ρ = fluid density (kg m⁻³)
g = gravitational field strength (m s⁻²)
h = depth below the fluid surface (m)
—-----------------------------------------------------------------
Because of this variation, the net upward force (upthrust) on the object can be determined by calculating the difference in forces on the top and bottom surfaces.
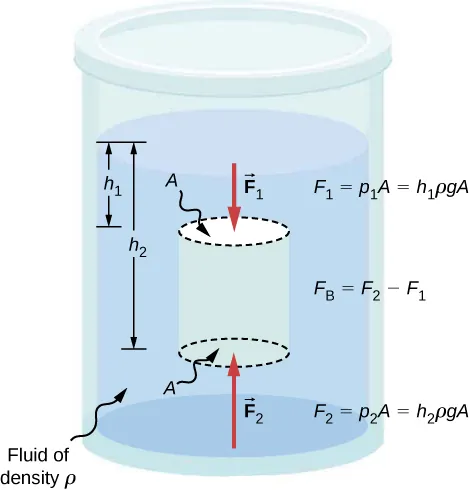
Hydrostatic pressure rises linearly with depth (p = ρgh), so the downward force at the top surface is smaller than the upward force at the bottom surface. The difference produces the buoyant force, FBF_BFB, while horizontal forces cancel. This diagram illustrates the pressure arrows and force labels that lead to upthrust. Source.
Resultant Upward Force
For a vertically oriented object of height h and cross-sectional area A, submerged in a fluid:
Pressure at top surface = ρg h₁
Pressure at bottom surface = ρg h₂
Force difference (upthrust) = Aρg (h₂ − h₁)
Since (h₂ − h₁) = height of the object submerged, the volume of displaced fluid equals A (h₂ − h₁). Therefore,
EQUATION
—-----------------------------------------------------------------
Upthrust (Fᵤ) = ρ g V
Fᵤ = upthrust (N)
ρ = fluid density (kg m⁻³)
g = gravitational field strength (m s⁻²)
V = volume of fluid displaced (m³)
—-----------------------------------------------------------------
This relation matches the weight of the displaced fluid, confirming Archimedes’ principle.
Floating, Sinking and Neutral Buoyancy
The interaction between upthrust and weight determines an object’s behaviour in a fluid:
Object sinks: Weight > Upthrust
Object floats: Weight < Upthrust
Object remains suspended: Weight = Upthrust
When an object floats, it displaces only enough fluid so that the upthrust equals its weight. In equilibrium, the object is said to have neutral buoyancy.
Conditions for Floating
The average density of the object is less than the density of the fluid.
The displaced volume of fluid produces an upthrust equal to the object’s weight.
The centre of mass lies below the centre of buoyancy to maintain stability.
Centre of Buoyancy: The point through which the resultant upthrust acts, corresponding to the centre of mass of the displaced fluid.
The alignment of the centre of mass and centre of buoyancy is essential for stability in floating objects such as ships or submarines.
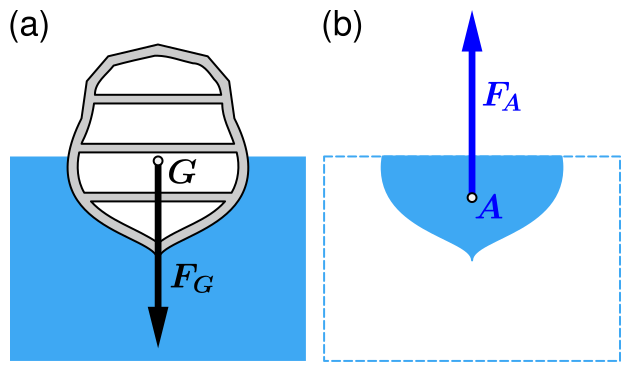
Diagram comparing centre of gravity (G) and centre of buoyancy (B) for a floating body. The upthrust acts vertically through B, which is the centroid of the displaced volume. This image focuses on the geometry behind stability discussed in the notes. Source.
Factors Affecting Upthrust
Several key factors influence the magnitude of the upthrust on an immersed object:
Density of the fluid (ρ): Greater fluid density increases the weight of displaced fluid and hence upthrust.
Volume displaced (V): Larger submerged volumes displace more fluid, leading to greater upthrust.
Gravitational field strength (g): Stronger gravity increases the weight of displaced fluid.
Therefore, upthrust depends directly on ρgV, as shown in the formula. These relationships explain why the same object may float in salt water but sink in fresh water.
Applications of Archimedes’ Principle
Archimedes’ principle is fundamental in both everyday and industrial contexts. Some key applications include:
Ship design and naval engineering: Ensures vessels displace sufficient water to support their weight while maintaining stability.
Submarines and diving equipment: Regulate buoyancy by adjusting the volume of air or water in ballast tanks.
Hydrometers: Measure the density of liquids based on the floating depth of a calibrated stem.
Airships and balloons: Employ the principle in gases, where the buoyant force is the weight of air displaced by the lighter gas inside.
In each case, balancing weight and upthrust is essential for achieving controlled movement or stability within a fluid medium.
Experimental Observation of Upthrust
Archimedes’ principle can be verified through simple laboratory experiments, often using a spring balance and a displacement can:
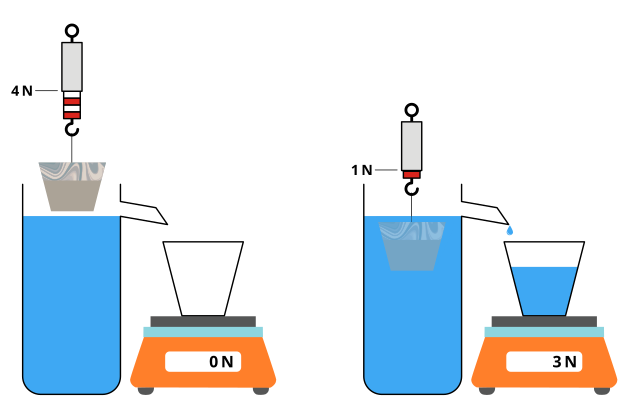
Measure the weight of an object in air.
Submerge it completely in water and record the apparent loss of weight.
Collect the displaced water and find its weight.
The loss in apparent weight equals the weight of displaced water, confirming that the upthrust equals the weight of the fluid displaced.
This experiment not only demonstrates Archimedes’ principle but also illustrates how pressure differences within fluids give rise to buoyant forces.
FAQ
The terms upthrust and buoyancy are closely related but not entirely interchangeable.
Upthrust refers specifically to the upward force exerted by a fluid on an object, opposing its weight. Buoyancy, on the other hand, describes the tendency of an object to float due to that force.
In most exam contexts, "upthrust" is the correct term for the force, while "buoyancy" can describe the effect or condition of floating. Both arise from the same physical mechanism — pressure differences within a fluid.
The centre of buoyancy is the point through which the resultant upthrust force acts because it represents the centroid of the displaced fluid volume.
The centre of mass is a property of the object itself, determined by how its mass is distributed.
When an object tilts, the shape of the displaced volume changes, moving the centre of buoyancy.
This shift creates a righting moment that can stabilise or destabilise floating bodies such as ships.
Thus, upthrust always acts vertically through the centre of buoyancy, not the centre of mass.
Yes, upthrust exists in air, as gases are fluids and exert pressure that increases with depth (height below a point).
However, because air density is extremely low (approximately 1.2 kg m⁻³), the weight of air displaced by most solid objects is tiny compared with their own weight.
Upthrust becomes significant only for:
Large-volume, low-density objects, such as hot air balloons or airships.
Precision measurements, where very small weight differences matter (e.g., mass calibration).
In everyday situations, upthrust in air is negligible and often ignored.
When an object is neutrally buoyant, its weight equals the upthrust even though it is completely submerged.
This can occur if the object’s density matches that of the surrounding fluid. Submarines and fish exploit this by adjusting their internal air or gas content:
Submarines change the water level in ballast tanks to control average density.
Fish use a swim bladder to adjust volume without altering mass.
In both cases, equilibrium is achieved when upthrust exactly balances weight.
A ship’s ability to float depends on its average density, not the density of its material.
Although metal is dense, ships are designed with hollow hulls that enclose large volumes of air. This reduces the overall density of the vessel below that of water.
The ship displaces a volume of water whose weight equals the ship’s total weight.
The resulting upthrust balances the downward force of gravity.
If water floods the hull, the average density increases and the ship may lose buoyancy and sink.
Practice Questions
Question 1 (2 marks)
A solid cube of volume 0.0020 m³ is completely submerged in water of density 1000 kg m⁻³.
Calculate the upthrust acting on the cube. State an appropriate unit for your answer.
Mark scheme:
Correct use of the equation Upthrust = ρ g V (1 mark)
Substitution and correct calculation: 1000 × 9.81 × 0.0020 = 19.6 N (1 mark)
Question 2 (5 marks)
A wooden block floats in water with 75% of its volume submerged.
(a) Explain, in terms of forces, why the block floats at a constant level. (2 marks)
(b) The density of water is 1000 kg m⁻³. Calculate the density of the wood. (2 marks)
(c) The block is then placed in oil of lower density. Describe and explain how its depth of immersion changes. (1 mark)
Mark scheme:
(a)
Weight of the block acts downwards and is balanced by upthrust acting upwards (1 mark)
The upthrust equals the weight when floating at equilibrium (1 mark)
(b)
Recognises that fraction submerged = ρ(wood) / ρ(water) (1 mark)
ρ(wood) = 0.75 × 1000 = 750 kg m⁻³ (1 mark)
(c)
The block sinks deeper in the oil so that a larger volume is displaced to produce the same upthrust (1 mark)

