OCR Specification focus:
‘Apply p = ρgh to fluids at rest; relate pressure differences to depth and density.’
Hydrostatic pressure describes how pressure increases with depth in a stationary fluid due to the weight of the fluid above. Understanding this principle is essential for explaining fluid behaviour in lakes, oceans, and hydraulic systems.
Pressure in Stationary Fluids
In a fluid at rest, every particle is acted upon by gravity, producing a downward force. This weight is transmitted through the fluid, creating pressure that increases with depth. Because the fluid is not moving, pressure at a point acts equally in all directions, a principle crucial to hydrostatics.
Hydrostatic pressure: The pressure exerted by a fluid at rest due to the weight of the fluid above a given point.
Pressure in a fluid is a scalar quantity, meaning it has magnitude but no direction. However, the force due to pressure always acts perpendicular to the surface it contacts.
The Hydrostatic Pressure Equation
The relationship between pressure, fluid density, gravitational field strength, and depth is expressed through a fundamental equation. This applies to any uniform gravitational field and stationary fluid of constant density.
EQUATION
—-----------------------------------------------------------------
Hydrostatic Pressure (p) = ρgh
p = hydrostatic pressure (Pa)
ρ = density of the fluid (kg m⁻³)
g = gravitational field strength (m s⁻²)
h = depth below the surface (m)
—-----------------------------------------------------------------
This equation shows that pressure at a given depth depends only on the density of the fluid, the gravitational field strength, and the depth below the surface, not on the shape or volume of the container.
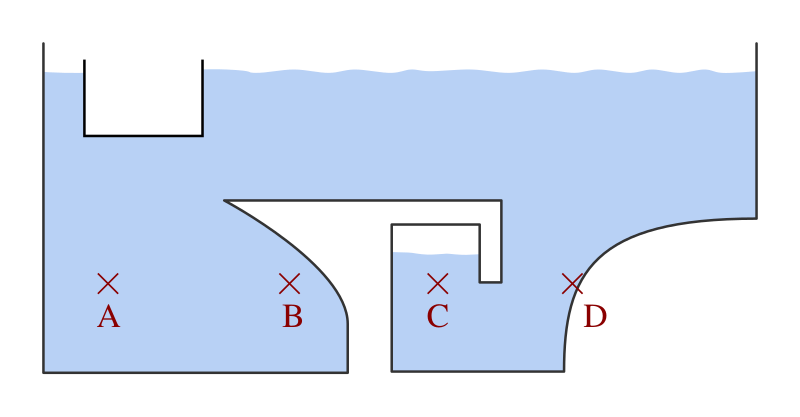
A clean schematic showing that points at the same depth share the same pressure in a stationary fluid. The diagram emphasises that hydrostatic pressure is independent of container shape and horizontal position, underlining the linear p–h relationship used in p = ρgh. Source.
Conceptual Basis of p = ρgh
To understand why pressure increases with depth, consider a column of fluid with cross-sectional area A and height h. The weight of this column is the force causing pressure at its base.
The weight (W) of the fluid column is given by W = mg. The mass (m) of the column can be expressed as m = ρV, where V = Ah is its volume. Substituting these expressions gives:
p = W / A = (ρAhg) / A = ρgh
This derivation demonstrates that pressure increases linearly with depth for a fluid of constant density.
Understanding the Variables
Depth (h)
The deeper an object is in a fluid, the greater the weight of fluid above it, and thus the greater the pressure. This is why divers experience increasing pressure as they descend underwater.
Density (ρ)
Fluids with higher density exert more pressure at a given depth. For example, sea water (ρ ≈ 1025 kg m⁻³) produces slightly more pressure than fresh water (ρ ≈ 1000 kg m⁻³) at the same depth.
Gravitational Field Strength (g)
On Earth, g ≈ 9.81 m s⁻², but it can vary slightly with altitude or location. On other planets, differences in g significantly alter hydrostatic pressure for the same depth and fluid.
Pressure Differences in Fluids
Hydrostatic pressure is not absolute but relative to another point in the same fluid. What matters in most applications is the difference in pressure between two depths.
EQUATION
—-----------------------------------------------------------------
Pressure Difference (Δp) = ρgΔh
Δp = pressure difference (Pa)
Δh = vertical height difference (m)
—-----------------------------------------------------------------
This expression is widely used in manometers, barometers, and fluid column experiments to determine relative pressures or densities.
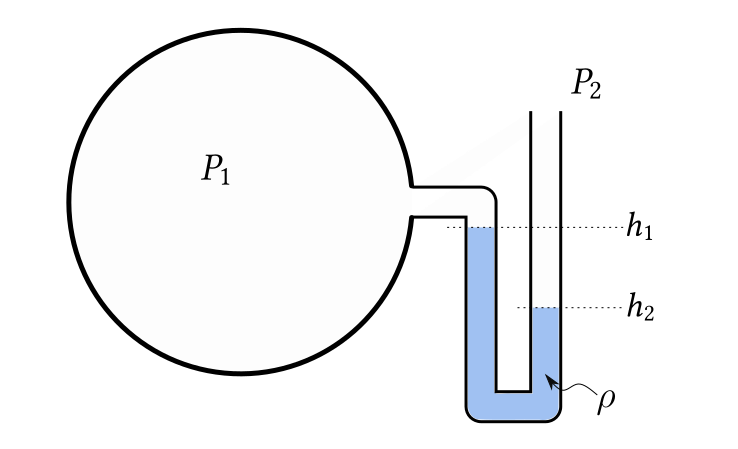
A labelled U-tube manometer showing two limbs with different fluid levels and the measured height difference h. The diagram highlights how gauge or differential pressure follows Δp = ρgΔh for a stationary fluid of density ρ, aligning with the OCR focus on relating pressure differences to depth. Source.
Key Features of Hydrostatic Pressure
Acts equally in all directions at a given point in the fluid.
Increases linearly with depth for fluids of constant density.
Independent of container shape — only depends on height, not the geometry of the vessel.
Dependent on density — denser fluids exert higher pressures for the same depth.
Zero at the surface if the fluid is open to the atmosphere (relative to atmospheric pressure).
These features explain phenomena such as why dams are thicker at the bottom, where pressure is greatest, and why submarines are reinforced to withstand immense external pressures at depth.
Relating Hydrostatic Pressure to Atmospheric Pressure
In open containers, the pressure within the fluid includes atmospheric pressure (pₐₜₘ) at the surface.
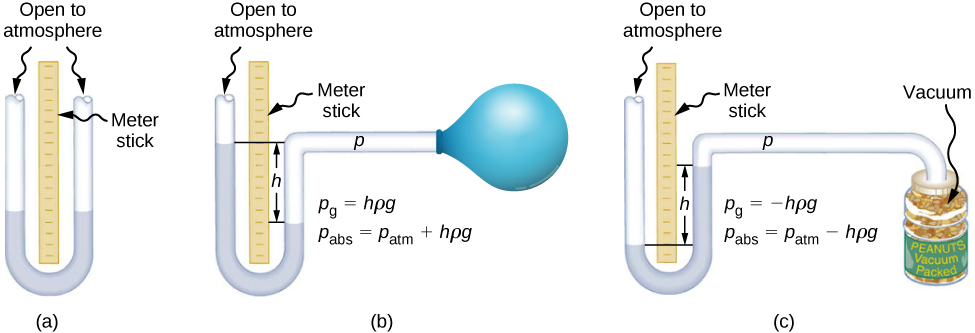
A textbook figure set showing open-tube manometers and a mercury barometer. It distinguishes gauge pressure (relative to pₐₜₘ) from absolute pressure, consistent with p_total = pₐₜₘ + ρgh. The figure includes additional examples, such as a balloon, illustrating the same hydrostatic principle beyond the core OCR requirement. Source.
The total pressure at a depth h is therefore:
EQUATION
—-----------------------------------------------------------------
Total Pressure (pₜₒₜₐₗ) = pₐₜₘ + ρgh
pₜₒₜₐₗ = absolute pressure at depth (Pa)
pₐₜₘ = atmospheric pressure (Pa)
—-----------------------------------------------------------------
For practical purposes, measurements often consider gauge pressure, which excludes atmospheric pressure. For example, a diver’s depth gauge measures pressure relative to the air at the surface.
Applications of Hydrostatic Pressure
Hydrostatic principles are central to many fields of physics and engineering. Common applications include:
Hydraulics: Predicting fluid pressure in pipes, pumps, and brake systems.
Oceanography: Measuring underwater pressure to estimate depth.
Meteorology: Using barometers to measure air pressure (a fluid under gravity).
Engineering design: Ensuring that tanks, dams, and submersibles can withstand pressure variations with depth.
Medical physics: Understanding blood pressure differences due to height changes in the circulatory system.
These applications all rely on the predictable relationship between pressure, density, and depth.
Factors Affecting Hydrostatic Pressure
Although p = ρgh assumes constant density, in reality, density can vary with temperature and pressure. In gases, this variation is significant; in liquids, it is small but measurable. For precise work:
Use local density values corrected for temperature.
Account for changes in g with altitude or latitude if necessary.
Recognise that non-uniform density leads to non-linear pressure–depth relationships.
Visualising Pressure in Depth
A pressure–depth graph for a fluid of constant density is a straight line through the origin, with a gradient equal to ρg. This linearity provides a simple visual method to compare fluids: steeper gradients represent denser fluids. The uniform slope confirms that each metre of additional depth adds the same increase in pressure.
FAQ
The equation assumes that the fluid is incompressible (constant density), at rest, and within a uniform gravitational field.
It also assumes that the depth h is measured vertically and that temperature variations do not cause changes in density. For most liquids under standard conditions, these assumptions hold true, but they become less accurate for gases or deep-sea conditions where compression occurs.
Hydrostatic pressure depends only on depth, density, and gravity, not on the container’s geometry.
At any given depth, the column of fluid above that point exerts the same weight per unit area, regardless of whether the container is wide, narrow, or irregularly shaped. This is often demonstrated by Pascal’s vases, which show that fluids in differently shaped vessels reach the same level when connected.
In gases, pressure still increases with depth, but the relationship is not linear because gas density changes significantly with pressure and temperature.
For small vertical distances, the change in gas pressure can be approximated by p = ρgh.
For larger height differences, such as in the Earth’s atmosphere, the barometric formula must be used, accounting for variable density.
Liquids, being nearly incompressible, maintain a constant density, so p = ρgh remains accurate over much greater depths.
Hydrostatic pressure is directly proportional to gravitational field strength (g).
On a planet with lower gravity, such as Mars, the pressure at a given depth would be smaller than on Earth for the same fluid and depth.
Conversely, in environments with stronger gravity, the pressure would increase proportionally.
This concept is particularly relevant in planetary physics and aerospace engineering, where gravitational differences affect fluid and atmospheric behaviour.
Temperature and salinity both influence the density (ρ) of water, which in turn affects hydrostatic pressure.
Colder water is denser, so pressure increases more rapidly with depth in colder regions.
Higher salinity also increases density, raising the pressure at the same depth.
In the ocean, these variations create density gradients, contributing to stratification and affecting the distribution of pressure, which influences currents and marine physics phenomena.
Practice Questions
Question 1 (2 marks)
A diver is 15 m below the surface of a lake. The density of the water is 1000 kg m⁻³ and the gravitational field strength is 9.81 m s⁻².
Calculate the increase in pressure on the diver compared to the surface.
Mark scheme:
Substitution into equation p = ρgh (1 mark)
p = 1000 × 9.81 × 15Correct final answer with appropriate unit (1 mark)
p = 1.47 × 10⁵ Pa (accept 147 kPa)
Question 2 (5 marks)
An open cylindrical tank contains oil of density 850 kg m⁻³. The tank is open to the atmosphere.
(a) Derive an expression for the pressure at a depth h in the oil. (2 marks)
(b) Explain why the pressure at the same depth is the same at all points in the oil, even if the tank has an irregular shape. (2 marks)
(c) State one practical example where hydrostatic pressure is important in engineering or nature. (1 mark)
Mark scheme:
(a)
Recognises that pressure arises due to the weight of the fluid above a point (1 mark)
Derives p = ρgh, showing that pressure increases linearly with depth (1 mark)
(b)
States that in a stationary (non-moving) fluid, pressure at a point acts equally in all directions (1 mark)
Explains that pressure depends only on depth and density, not on the container’s shape (1 mark)
(c)
Gives one suitable example, such as dam design, submarine hulls, or blood pressure in the body (1 mark)

