OCR Specification focus:
‘State and apply Hooke’s law within elastic limit; identify proportional region and limit of proportionality.’
Hooke’s law defines the relationship between the force applied to an elastic material and its resulting extension, forming the foundation for understanding elasticity, material behaviour, and mechanical equilibrium in physics.
Hooke’s Law and Elastic Behaviour
The Concept of Elasticity
When a material is subjected to a tensile or compressive force, it experiences a change in length. If, after removing the force, the material returns to its original shape, this behaviour is known as elastic deformation. If it remains permanently deformed, it has undergone plastic deformation.
The study of Hooke’s law focuses on elastic deformation, which occurs when the extension is directly proportional to the applied force, up to a certain limit.
Hooke’s Law Defined
Hooke’s Law: Within the elastic limit, the extension of an elastic object is directly proportional to the force applied to it.
This means that doubling the applied force will double the extension, provided the material is not stretched beyond its elastic limit. This relationship can be expressed using the following equation.
EQUATION
—-----------------------------------------------------------------
Hooke’s Law (F = kx)
F = kx
F = Force applied (newtons, N)
k = Force constant or spring constant (newtons per metre, N m⁻¹)
x = Extension of the material (metres, m)
—-----------------------------------------------------------------
The spring constant k is a measure of stiffness; a higher value of k indicates a stiffer material or spring.
A minimal diagram of a spring under load showing extension (x) and associated force, highlighting the variables in Hooke’s law (F = kx). Use alongside the equation to link symbols to the physical setup. No proportional-limit markers are shown (that content is in the graph images). Source.
The Proportional Region and the Limit of Proportionality
The Linear Relationship
When plotting a force–extension graph for a material obeying Hooke’s law, the initial portion of the graph is a straight line through the origin. This region, known as the proportional region, represents where F ∝ x, meaning force and extension are in a fixed ratio.
Within this region:
The gradient of the line equals the force constant (k).
The material will return to its original length once the force is removed.
The deformation is entirely elastic.
The Limit of Proportionality
As the force increases, a point is reached beyond which the relationship between force and extension is no longer perfectly proportional. This point is known as the limit of proportionality.
Limit of Proportionality: The maximum force beyond which extension is no longer directly proportional to the applied force, even though the material may still return to its original shape when unloaded.
Beyond this point, the graph begins to curve, indicating that Hooke’s law no longer applies, although the material may still behave elastically up to a further limit—the elastic limit.
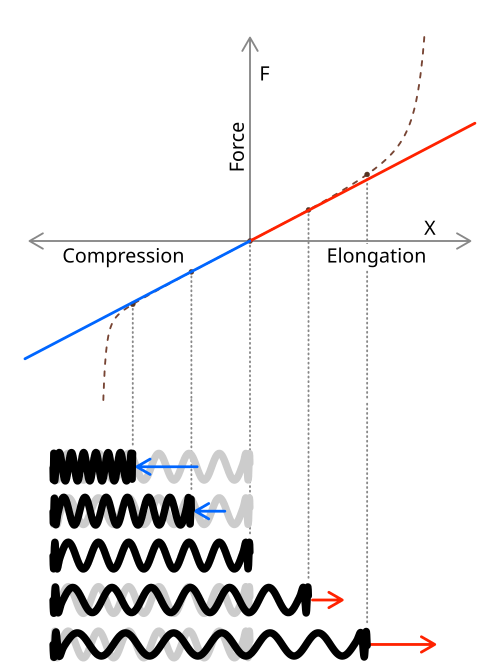
Annotated force–extension plot with a straight-line proportional region and a dashed curve indicating real-spring nonlinearity beyond the limit of proportionality. The coloured halves illustrate compression and extension; compression is extra detail not required by the syllabus but reinforces symmetry. The bottom row shows corresponding spring states for selected points on the graph. Source.
Distinguishing the Elastic Limit from the Limit of Proportionality
It is important to note that the elastic limit and limit of proportionality are not always the same point.
Limit of proportionality: Marks the end of the linear (proportional) region.
Elastic limit: Marks the point beyond which the material will not return to its original shape after unloading.
In many metals and springs, these two points are close, but distinct. Up to the elastic limit, all deformation is reversible. Beyond it, plastic deformation begins, and permanent changes in shape occur.
Applying Hooke’s Law in Practice
Determining the Force Constant
The force constant (k) can be determined experimentally by measuring the force applied and the corresponding extension of a spring or wire. The steps typically involve:
Measuring the natural length of the spring without load.
Hanging known masses from the spring and recording the new lengths.
Calculating the extension for each load.
Plotting a force–extension graph and finding the gradient of the linear region.
The gradient gives the force constant k. A steeper gradient represents a stiffer spring.
Units and Dimensional Considerations
The relationship F = kx shows that:
1 N m⁻¹ means that 1 N of force causes 1 m of extension.
For practical laboratory experiments, extensions are often measured in millimetres, and conversions to metres must be made carefully.
When analysing data, proportionality should be confirmed by checking that the ratio F/x remains constant up to the limit of proportionality.
Behaviour Beyond the Elastic Region
Plastic Deformation
Once the elastic limit is exceeded, additional applied force causes plastic deformation. The atoms within the material move relative to one another and do not return fully to their original positions when the force is removed. This region is non-linear and irreversible.
Temporary and Permanent Deformation
Elastic deformation: Temporary and reversible.
Plastic deformation: Permanent and irreversible.
Beyond the elastic limit, Hooke’s law is no longer valid, and the material may eventually reach a fracture point where it breaks.
Practical Relevance of Hooke’s Law
Engineering and Design
Hooke’s law underpins the design of many mechanical systems, such as:
Suspension systems in vehicles.
Measuring instruments like force meters.
Structural components that must remain within elastic limits to avoid damage.
By ensuring that operating stresses stay within the proportional region, engineers can maintain both accuracy and safety in material performance.
Everyday Applications
Spring balances use Hooke’s law to measure weight directly from extension.
Elastic bands display limited proportionality before significant non-linear behaviour.
Polymers and rubbers often have wide non-linear regions, illustrating deviations from Hooke’s ideal relationship.
Graphical Representation and Key Features
A force–extension graph clearly illustrates the concepts of proportionality and elastic behaviour:
The initial straight-line region confirms Hooke’s law.
The point where the curve begins marks the limit of proportionality.
The elastic limit lies slightly beyond this, after which permanent deformation occurs.
The area under the curve (though not part of this subsubtopic) represents the work done on the material, which becomes stored as elastic potential energy within the elastic region.
Summary of Key Concepts
Hooke’s law describes a linear relationship between force and extension within the elastic limit.
The force constant (k) characterises the stiffness of a material or spring.
The limit of proportionality marks where F ∝ x ceases to be true, though elasticity may remain.
Elastic and plastic regions define reversible and permanent material behaviour, respectively.
FAQ
The spring constant (k) measures a spring’s stiffness — the larger its value, the greater the force needed to produce a given extension.
It depends on several factors:
Material: Metals like steel generally have higher k values than softer materials.
Geometry: Thicker coils or shorter springs resist deformation more strongly.
Number of coils: More coils reduce stiffness since the load is distributed over a longer wire length.
Temperature: Higher temperatures can lower k slightly due to reduced material rigidity.
The linear relationship holds while atomic bonds stretch proportionally to the applied force. Beyond this region, bonds begin to rearrange or slip, causing the extension to increase more quickly.
This marks the limit of proportionality, where Hooke’s law no longer applies even though the spring may still return to its original shape if unloaded before reaching the elastic limit.
Common errors include:
Parallax error when reading the extension scale.
Zero error if the ruler or spring length is not properly aligned before loading.
Non-uniform spring stretching caused by uneven coiling or friction at the clamp.
To reduce errors:
Use a pointer attached to the spring to measure extension accurately.
Take multiple readings and plot a best-fit line to find k from the gradient.
Stiffness refers to how resistant a material is to deformation — quantified by the spring constant k. A stiffer spring has a higher k value.
Strength is the maximum stress or force the material can withstand before breaking.
A material can be very stiff but not strong (e.g., brittle glass), or strong but flexible (e.g., mild steel). Hooke’s law only describes stiffness, not the ultimate strength of materials.
When stretched past the elastic limit, the atomic bonds within the material begin to permanently rearrange.
Some energy is used to move atoms into new equilibrium positions, producing a small plastic deformation.
As a result, even though the spring may appear almost normal, its internal structure is altered, and it will not completely recover its original length once the load is removed.
Practice Questions
Question 1 (2 marks)
A student hangs a spring vertically and measures its extension for a range of applied forces.
State Hooke’s law and describe the condition under which it is valid.
Mark scheme:
(1 mark) Correctly states that Hooke’s law states the extension (or compression) of an elastic material is directly proportional to the applied force.
(1 mark) States that the law is valid only within the material’s elastic limit or proportional region.
Question 2 (5 marks)
A helical spring has a force constant k of 40 N m⁻¹.
(a) Calculate the force required to produce an extension of 3.0 cm.
(b) The student then increases the applied force until the spring no longer obeys Hooke’s law.
(i) State the name of the point at which the spring stops obeying Hooke’s law but will still return to its original length when the force is removed.
(ii) Describe and explain how the force–extension graph changes beyond this point.
Mark scheme:
(a)
(1 mark) Correct substitution into F = kx (F = 40 × 0.03).
(1 mark) Correct answer: F = 1.2 N, with correct unit.
(b)(i)
(1 mark) Correctly identifies the limit of proportionality.
(b)(ii)
(1 mark) Describes that the graph begins to curve and is no longer a straight line.
(1 mark) Explains that extension increases more rapidly with force because the proportional relationship between force and extension is lost, though the material remains elastic until the elastic limit is reached.

