Concavity describes how a function bends, and the second derivative provides a powerful tool for analyzing this curvature. Understanding concavity helps reveal deeper structure in a function’s behavior.

Understanding Concavity Using the Second Derivative

Concavity is a fundamental aspect of a function’s shape that reveals how its graph bends and how its rate of change itself is changing. In AP Calculus AB, students use the second derivative, written as $f''(x)$, to classify concavity on intervals and interpret the resulting geometric behavior. The AP specification emphasizes that positive second derivative values correspond to concave up behavior, whereas negative second derivative values correspond to concave down behavior. By mastering this connection, students gain insight into the underlying structure of functions beyond simple increases or decreases.

The Idea of Concavity

Concavity describes whether a graph bends upward or downward. When a function bends upward like a cup, it is concave up; when it bends downward like an upside-down bowl, it is concave down.

A pair of graphs contrasts concave-down and concave-up curves. The concave-down curve corresponds to intervals where f''(x) < 0, while the concave-up curve corresponds to f''(x) > 0. The term “convex” appears in the diagram, which is standard in higher mathematics and slightly beyond AP scope. Source.

A function’s concavity is not merely a visual characteristic; it communicates how the slope of the first derivative behaves. If slopes are becoming larger (even if negative), the function is concave up. If slopes are becoming smaller, the function is concave down.

Using the Second Derivative to Determine Concavity

The second derivative measures the rate of change of the first derivative. Therefore, signs of the second derivative tell us precisely how the slope is evolving.

When analyzing concavity, the sign of $f''(x)$ is the key piece of information. One does not rely on exact values but on whether $f''(x)$ is positive, negative, or zero.

Between any equation or definition block, include at least one meaningful sentence; this sentence fulfills that requirement and prepares the reader for operational steps.

Concave Up Behavior

A graph is concave up when its slopes increase as $x$ increases. This does not mean the function itself must be increasing; it simply means the slope becomes less negative or more positive.

Key features of concave up intervals include:

• f''(x) > 0, meaning the first derivative is increasing.

• The graph opens upward, often described as “holding water.”

• Tangent lines lie below the graph on the interval.

• The rate of change becomes steeper in the positive direction or less steep in the negative direction.

Concave Down Behavior

A graph is concave down when slopes decrease as $x$ increases. Again, the function need not be decreasing; what matters is that the slope becomes less positive or more negative.

Characteristics of concave down intervals include:

• f''(x) < 0, meaning the first derivative is decreasing.

• The graph opens downward, forming a “cap.”

• Tangent lines lie above the graph on that interval.

• The rate of change becomes steeper in the negative direction or less steep in the positive direction.

Intervals of Concavity

Determining intervals of concavity typically involves studying the sign of the second derivative across its domain. Students rely on critical points of $f''(x)$ to organize this information.

To analyze concavity:

• Identify where $f''(x)$ is zero or undefined; these mark potential changes.

• Construct a sign chart for $f''(x)$ across resulting intervals.

• On each subinterval, test the sign of $f''(x)$ to determine concavity.

• Interpret concavity consistently with the sign chart and derivative behavior.

These steps allow a structured and reliable interpretation of a function’s curvature across any interval where it is twice differentiable.

Relationship Between the First and Second Derivatives

Because $f''(x)$ measures how $f'(x)$ changes, concavity provides insight into the motion of slopes.

Important relationships include:

• If the first derivative is increasing, the function is concave up.

• If the first derivative is decreasing, the function is concave down.

• Concavity helps anticipate where extrema and inflection points may occur, though those topics are treated separately in other subsubtopics.

• A deeper understanding of concavity strengthens interpretation of graphs, tables, and symbolic information.

When students combine first- and second-derivative information, they build a complete picture of how a function behaves, reinforcing the central role of concavity in calculus.

Practical Interpretation of Concavity

Understanding concavity using the second derivative helps students interpret function behavior from multiple representations. It allows them to describe how a graph bends, how slopes change, and how rates of change of rates of change behave. Whether reading a graph, analyzing a derivative table, or working from an algebraic expression, concavity becomes an essential descriptive tool.

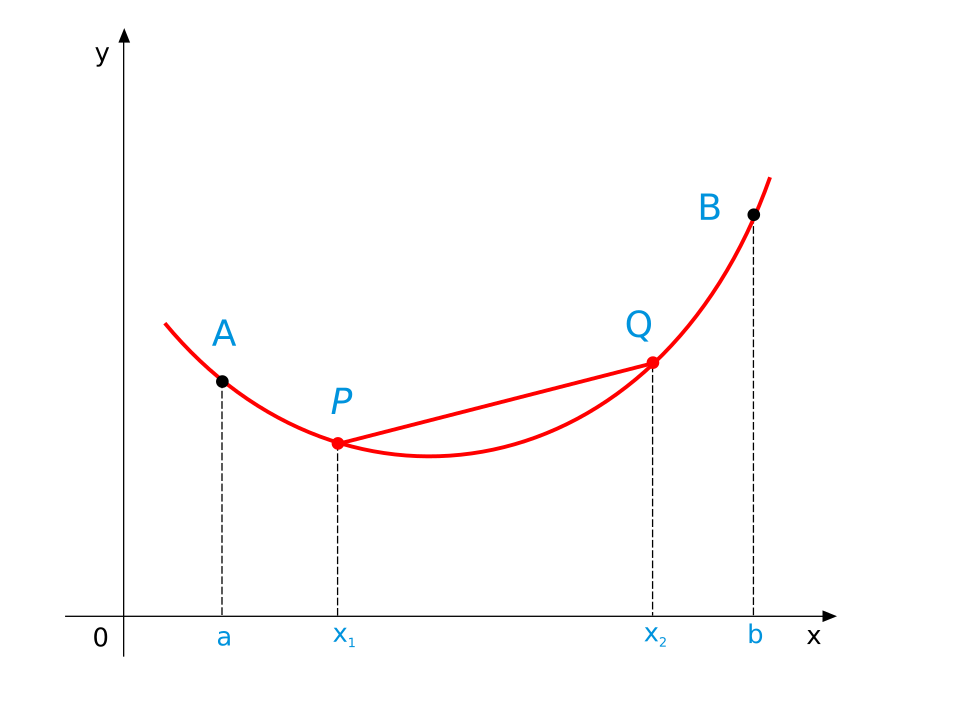
This graph depicts a smooth concave-up function. The curve’s upward bend aligns with intervals where f''(x) > 0. The connection to the second derivative is provided by the surrounding discussion, as the image itself includes only the geometric shape. Source.

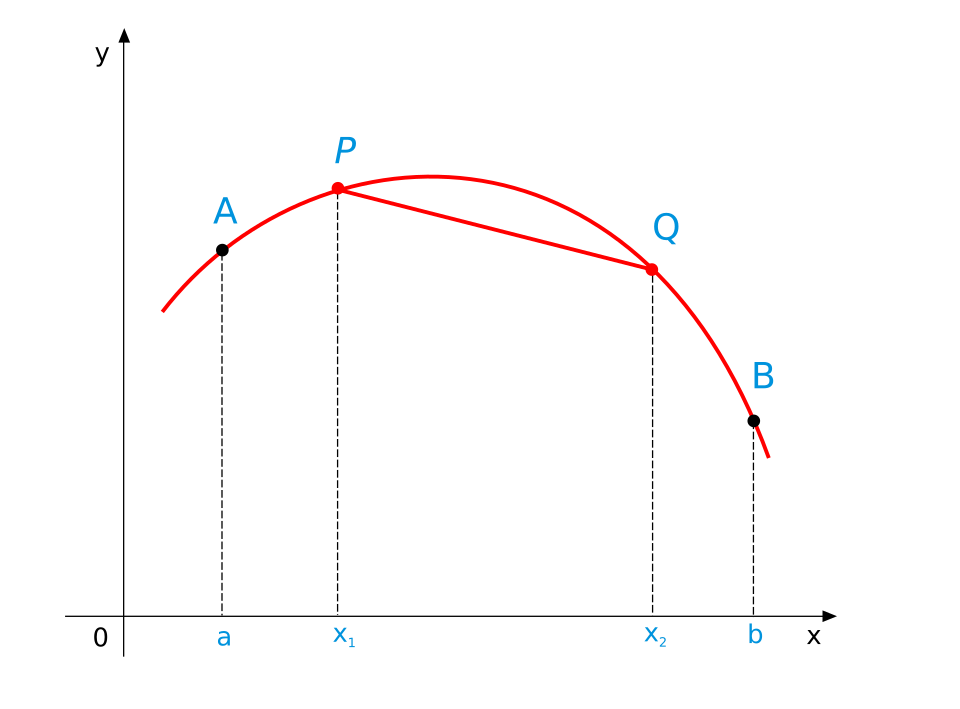
This graph shows a concave-down function. The downward arch reflects intervals where f''(x) < 0. The diagram focuses solely on the geometric shape, leaving derivative interpretation to the accompanying notes. Source.