AP Syllabus focus:
‘Values or graphs of f′ and f″ can be used together to describe where a function bends upward or downward and how its rate of change is itself changing.’
Concavity describes how a graph bends, and understanding it requires interpreting derivative information. By analyzing tables or graphs of f′ and f″, we identify where a function curves upward or downward.
Understanding Concavity Through Derivative Information
Concavity reveals whether a function bends upward or downward, reflecting how the function’s rate of change evolves. When using derivative data rather than explicit formulas, recognizing consistent patterns in f′ and f″ becomes essential for interpreting behavior from graphical or numerical representations.
Concavity from the First Derivative
A function’s concavity can be inferred from how its first derivative behaves across an interval. If f′ is increasing, the function is bending upward; if f′ is decreasing, the graph bends downward.
Concave Up: The graph of a function bends upward on intervals where the rate of change increases.
A table showing increasing values of f′—even without the actual function values—indicates upward bending because the slope is rising. Conversely, decreasing derivative values signal downward bending because the slope is becoming smaller or more negative.
Concavity from the Second Derivative
Graphs or tables of the second derivative, f″, provide even more direct information about concavity. Positive second-derivative values indicate upward bending, while negative values indicate downward bending.
Concave Down: The graph of a function bends downward on intervals where the rate of change decreases.
A single equation may accompany this reasoning when helping students relate sign information to concavity.
= Input variable
By reading a graph of f″, students note where it lies above or below the x-axis to determine how the function behaves on corresponding intervals of x.
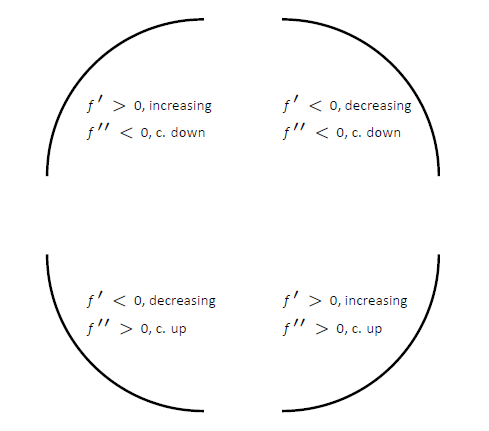
This multi-panel diagram compares graphs of , , and to illustrate how increasing or decreasing behavior combines with concave up or concave down curvature. Students can see that intervals where correspond to upward bending of , while intervals where correspond to downward bending. The figure also includes some additional detail about how changes on these intervals, extending slightly beyond the syllabus but reinforcing the same reasoning. Source.
Using Tables to Describe Concavity
Tables organize derivative information numerically and allow students to track how the slope or curvature changes step by step.
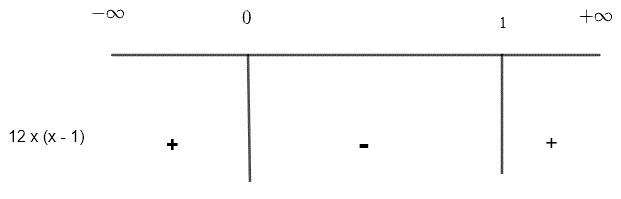
This sign table lists intervals for , the sign of , and the corresponding concavity of the graph of . Positive entries indicate concave up behavior, while negative entries indicate concave down behavior across each interval. The table includes a specific example with endpoint values, slightly beyond syllabus requirements but still fully aligned with the core concept of using derivative signs to determine concavity. Source.
When interpreting concavity from a table:
Identify whether f′ is increasing or decreasing across consecutive x-values.
Observe the sign of f″ if the table provides second-derivative values.
Note intervals rather than isolated points to understand overall graph shape.
Combine data trends to infer whether the function bends up or down.
Because tables offer discrete data, students should focus on patterns, not isolated derivative values. For instance, several positive and rising f′ values across increasing x-values indicate a consistent upward bend.
Using Graphs to Describe Concavity
When given graphs of f′ or f″, visual cues communicate concavity efficiently. A graph of f′ reveals concavity by showing whether the derivative is sloping upward or downward:
f′ sloping upward → graph of f is concave up.
f′ sloping downward → graph of f is concave down.
If f″ is graphed, concavity becomes even more straightforward to determine:
f″ above the x-axis → concave up.
f″ below the x-axis → concave down.
Graphical analysis helps students visualize curvature by connecting slope changes with geometric bending. This reinforces the idea that concavity concerns the behavior of the derivative, not the original function alone.
Coordinating Information from Multiple Representations
Strong understanding comes from linking tables and graphs of derivatives. When reading multiple forms of data, students should:
Verify that the numerical trend in a table matches what the graph depicts.
Check that positive or negative regions of f″ on a graph align with rising or falling patterns in tabulated values.
Interpret all data within the same intervals to avoid contradictions.
Tables may emphasize precise numerical change, while graphs emphasize broader shape, but both contribute to a coherent picture of concavity.
Describing Concavity Clearly in Words
Precise communication is important when interpreting derivative data. Effective explanations should reference both the function and the derivative explicitly. Students should:
State the interval being analyzed.
Indicate whether the conclusion arises from f′ or f″.
Explain how the sign or trend of the derivative determines concavity.
Avoid vague descriptions such as “the graph curves up” without linking this to derivative behavior.
Clear description reinforces understanding of how concavity arises from measurable changes in the rates of change.
Recognizing Shifts in Concavity Using Data
Tables or graphs may also reveal where concavity switches direction. Detecting these transitions requires carefully noticing changes in derivative behavior:
A change in the sign of f″ suggests a shift between concave up and concave down.
A change from increasing to decreasing patterns in f′ also marks potential bending changes.
Shifts must occur across intervals; isolated values cannot confirm changing concavity.
Although identifying the precise point where the concavity changes belongs to other subsubtopics, recognizing these shifts within tables or graphs prepares students to understand curvature more deeply.
Synthesizing Understanding for AP Practice
When interpreting concavity in AP Calculus AB contexts, students should consistently integrate information from any provided representation:
From tables: look for derivative trends.
From graphs: focus on sign and shape.
From combined data: ensure both agree on upward or downward bending.
Because the AP syllabus emphasizes using tables and graphs, mastering these interpretive skills strengthens students’ ability to analyze functions without relying solely on algebraic formulas.
FAQ
Small changes in recorded values do not always indicate a meaningful change in concavity. What matters is the overall trend across an interval rather than point-to-point noise.
If f' increases consistently over several entries, the function is concave up; if it decreases consistently, the function is concave down.
When fluctuations occur, focus on whether the broader pattern shows a sustained rise or fall rather than reacting to isolated irregularities.
Yes. Concavity is determined by how f' changes, not its sign.
If f' is negative but increasing (for example, from -6 to -2), the slope is becoming less steep, meaning the graph bends upward.
Negative values simply indicate that the function is decreasing overall; they do not prevent concave-up behaviour.
Focus on the qualitative shape of the f' curve rather than exact positions.
Look for:
• whether the curve is trending upward or downward
• changes in this trend across intervals
• consistent rising or falling behaviour
Even with rough drawings, concavity depends on directional changes, not numerical accuracy.
Tables and rough sketches may show apparent sign or trend changes due to sampling gaps, scaling issues, or approximate plotting.
Concavity only changes when the trend of f' or the sign of f'' shifts consistently across a neighbourhood.
If the suggested change appears at a single point without surrounding support, it is likely an artefact of limited data rather than a true change in concavity.
Use each representation to verify the conclusions of the other.
From the table: identify whether f' increases or decreases across intervals.
From the graph: check visually whether the slope of f' aligns with the numerical pattern.
If both agree, concavity is reliably determined; discrepancies may indicate reading errors, poor scaling, or insufficient data resolution.
Practice Questions
Question 1 (1–3 marks)
A table of values for the derivative f'(x) of a function f is shown below:
x: 1, 2, 3, 4
f'(x): -4, -1, 2, 5
Using only the information in the table, determine on which intervals the graph of f is concave up or concave down. Justify your answer in terms of the behaviour of f'.
Question 1 (1–3 marks)
• 1 mark: Correctly identifies that f is concave down on (1, 2) because f'(x) is increasing from -4 to -1 but still becoming "less negative", indicating its slope is increasing.
• 1 mark: Correctly identifies that f is concave up on (2, 4) because f'(x) increases from -1 to 5.
• 1 mark: Provides a correct justification referring explicitly to whether f' is increasing or decreasing.
Question 2 (4–6 marks)
The graph of f'(x), the derivative of a function f, is shown as a smooth curve passing through the following key features:
• f'(x) decreases on the interval (-2, 0)
• f'(x) increases on the interval (0, 3)
• f'(x) is negative for x < 1 and positive for x > 1
(a) Determine the intervals where the graph of f is concave up and where it is concave down.
(b) State the x-value of any point where the concavity of f changes, and explain why.
(c) Briefly describe how the change in the behaviour of f' affects the shape of the graph of f.
Question 2 (4–6 marks)
Part (a)
• 1 mark: States f is concave down on (-2, 0) because f'(x) is decreasing.
• 1 mark: States f is concave up on (0, 3) because f'(x) is increasing.
Part (b)
• 1 mark: Identifies x = 0 as the point where concavity changes.
• 1 mark: Justifies that this is where f' changes from decreasing to increasing.
Part (c)
• 1 mark: Describes that when f' switches from decreasing to increasing, the graph of f changes from bending downward to bending upward.
• 1 mark: Provides an additional correct statement about the shape of f, such as that the point where the behaviour changes corresponds to a bend in the graph (a point where curvature changes).

