AP Syllabus focus:
‘To locate possible points of inflection, solve f″(x)=0 or find where f″(x) does not exist, then check whether the sign of f″(x) actually changes across those x-values.’
Identifying points of inflection reveals where a function’s curvature changes. Using derivatives, we determine candidate points and verify actual concavity shifts essential for understanding a graph’s overall behavior.
Finding Points of Inflection Using Derivatives
Points of inflection are key features in the study of function behavior because they mark where a graph switches its concavity, changing how the curve bends. AP Calculus AB requires students to determine these points using second derivative analysis, ensuring both algebraic reasoning and justified conclusions based on concavity.
Understanding What a Point of Inflection Represents
A point of inflection is a point on the graph of a function where the concavity changes from concave up to concave down, or from concave down to concave up. This change in curvature reflects a shift in how the function's rate of change is itself changing.
Point of Inflection: A point on the graph of a function where concavity changes, provided the function is defined near that point.
A function is concave up when it bends upward like a cup and concave down when it bends downward like a cap.
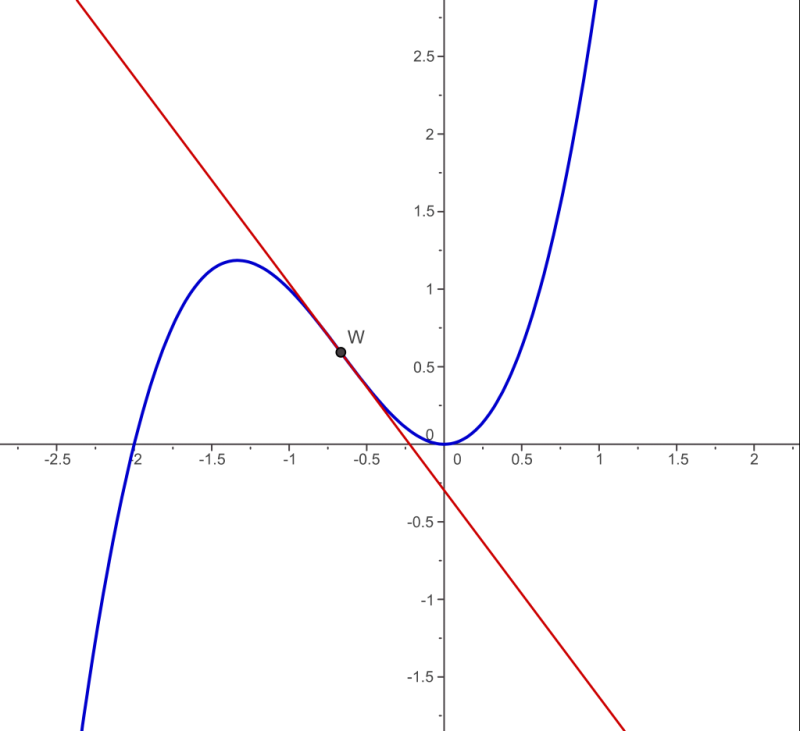
This graph shows a function with a single point of inflection where the curvature switches from concave down to concave up. The axes and smooth curve emphasize how concavity describes the bending of the graph. The explicit formula is included on the source page but is not required by the syllabus. Source.
Using the Second Derivative to Identify Candidates
To begin locating possible inflection points, we analyze the second derivative, because concavity is determined by the sign of . The AP specification states that we must “solve or find where does not exist” as the first step. These values are candidates, not confirmed inflection points.
= Function is concave up
= Function is concave down
Between the definition of concavity and the equation above, it is essential to recognize that concavity depends on an entire interval, not just a single value of . Candidates arise where concavity might shift.
Confirming a Point of Inflection
A candidate value becomes a true point of inflection only if the sign of changes on either side of that value. Simply having is not enough; in fact, many functions satisfy this condition without experiencing any concavity change.
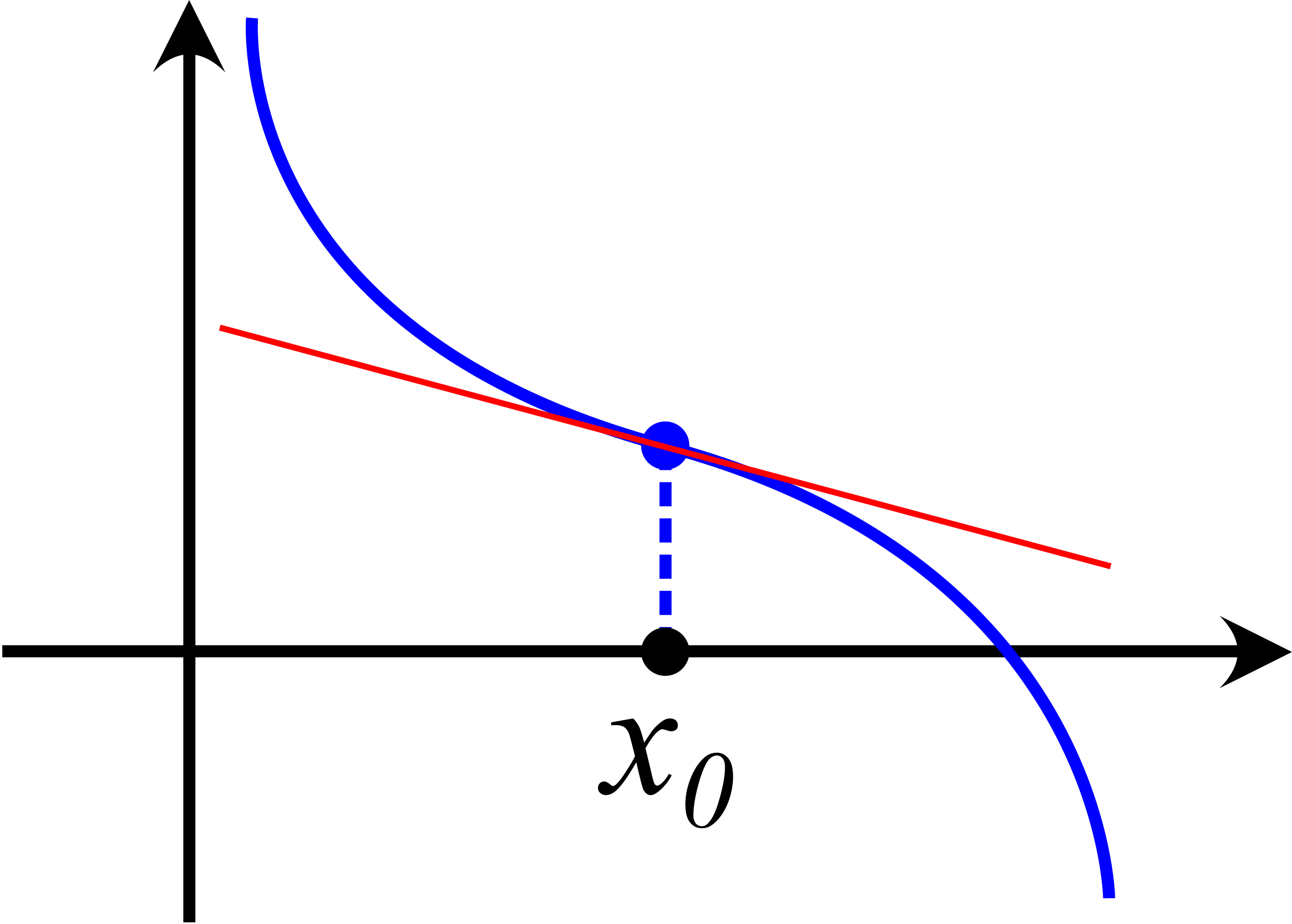
This diagram illustrates a non-stationary point of inflection, where concavity changes even though the tangent line is not horizontal. It demonstrates that inflection points are defined by changes in rather than by . The presence of a non-horizontal tangent adds extra detail beyond the minimum syllabus requirement. Source.
The Role of Domain and Function Definition
Even if concavity changes at a specific value, the function must be defined at that point to count it as an inflection point. AP Calculus AB emphasizes checking definitions carefully, especially for piecewise or implicitly defined functions.
If a function has a hole or vertical asymptote at , then cannot be a point of inflection, even if concavity changes around it. The point must lie on the curve itself.
Using Sign Charts to Support Justification
A sign chart for the second derivative provides an organized display of how concavity behaves over intervals. This tool is especially important in written justifications, allowing students to reference interval signs clearly and accurately.
A well-constructed sign chart:
Lists candidate points in numerical order
Tests in each interval between candidates
Uses plus and minus signs to represent concavity behavior
Visually demonstrates the sign change required for an inflection point
When the Second Derivative Is Difficult to Compute
In some cases, may be complex or unavailable. Students may still locate inflection points by interpreting the behavior of , because a graph is concave up when is increasing and concave down when is decreasing. This approach aligns with the conceptual link between concavity and the rate of change of the first derivative.
Even without a closed-form expression for , students can apply the same logic: concavity changes when the direction of change in switches.
Practical Process for AP-Ready Analysis
The following workflow aligns directly with syllabus expectations and supports correct AP exam justifications:
Compute from the given function
Solve to find potential inflection points
Identify values where does not exist but the function is defined
Create a second-derivative sign chart or test values around each candidate
Check for a sign change in across each candidate
Verify that the function is defined at each confirmed value
State the final inflection points using correct mathematical justification referencing concavity
Importance of Concavity Shifts in Function Analysis
Identifying inflection points offers deeper insight into the structure and behavior of a function. Inflection points mark transitions in the function’s curvature, reflecting how the rate of change accelerates or decelerates. This understanding strengthens graph analysis, supports optimization reasoning, and enriches interpretation of complex functional behavior.
FAQ
A flat tangent occurs when the first derivative is zero, but this alone does not indicate a point of inflection. A point of inflection requires a change in concavity, which must be verified by checking the sign of the second derivative on either side of the point.
A flat tangent without a change in concavity means the point is not an inflection point, even though the slope is zero.
A point of inflection still requires that the function be defined at that point, but differentiability is not strictly necessary. Concavity is determined by the behaviour on either side of the point.
However, if the graph is not smooth (for example, a sharp corner), many exam contexts will avoid treating such points as inflection points unless the concavity change is unambiguous.
Yes. If the second derivative does not exist at a point but has different signs on the intervals immediately to the left and right, the point can still be classified as an inflection point.
This scenario often arises in functions involving roots or piecewise definitions where the second derivative fails at the joining point.
A sign chart helps visualise concavity over various intervals, especially when the second derivative has several roots or undefined points. To use it efficiently:
• Find all values where the second derivative is zero or undefined.
• Test a representative point in each interval.
• Compare the signs sequentially to identify all places where concavity changes.
Yes, but only if the second derivative is undefined somewhere within that interval. If the second derivative is continuous, concavity cannot change without crossing zero.
When the second derivative is discontinuous, concavity may shift due to a jump or vertical asymptote, creating additional inflection points not captured by solving the equation f'' = 0 alone.
Practice Questions
Question 1 (1–3 marks)
A function g is twice differentiable on the real line. It is known that g''(2) = 0. The sign of g''(x) is positive for x < 2 and negative for x > 2.
(a) Determine whether x = 2 is a point of inflection for g. Justify your answer.
Mark scheme for Question 1
• 1 mark: States that g'' changes sign at x = 2.
• 1 mark: Concludes that x = 2 is a point of inflection because concavity changes.
• 1 mark: Provides a clear justification referring to concavity (concave up for x < 2 and concave down for x > 2).
Question 2 (4–6 marks)
Let f be a function defined and twice differentiable on the interval 0 < x < 6. Its second derivative is given by
f''(x) = (x - 2)(x - 5).
(a) Identify all candidate x-values where f might have a point of inflection.
(b) Determine which, if any, of these values are actual points of inflection.
(c) Explain the concavity of f on each subinterval determined by these points.
Mark scheme for Question 2
• 1 mark: Correctly identifies candidates x = 2 and x = 5 by solving f''(x) = 0.
• 1 mark: Tests the sign of f''(x) on intervals (0,2), (2,5), and (5,6).
• 1 mark: States that f''(x) is positive on (0,2), negative on (2,5), and positive on (5,6).
• 1 mark: Concludes that both x = 2 and x = 5 are points of inflection because the sign of f''(x) changes at each value.
• 1 mark: Clearly states the concavity: concave up on (0,2), concave down on (2,5), concave up on (5,6).
• 1 mark: Provides full, logically structured reasoning linking sign changes of f'' to concavity changes.

