Understanding points of inflection helps describe how a function bends and transitions between concave up and concave down behavior, revealing essential structural changes in a graph’s curvature.

Core Idea of Points of Inflection

A point of inflection is a location on the graph of a function where the curvature changes direction. In AP Calculus AB, this concept is directly tied to concavity, which describes how the graph bends. A point of inflection signals a shift in the behavior of the second derivative, and recognizing it allows us to better understand how a function grows, curves, and transitions across its domain.

A graph is concave up when it opens upward like a cup and concave down when it bends downward like an arch. The transition between these two behaviors marks potential points of inflection.

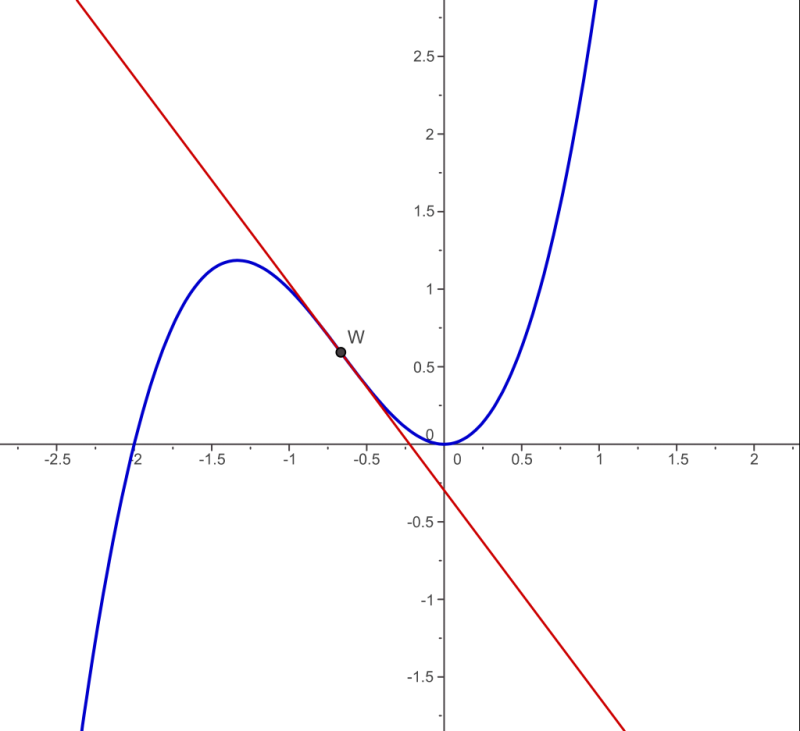
A graph of the function $f(x) = x^3 + 2x^2$ with its point of inflection highlighted, where the curve changes from concave down to concave up. The axes and smooth curve visually reinforce how concavity relates to the shape of the graph. This image contains no significant extra detail beyond illustrating a single, clearly defined inflection point. Source.

Concavity and Its Role in Identifying Inflection Points

Concavity is determined using the second derivative of a function. When the second derivative is positive over an interval, the function is concave up; when negative, the function is concave down. A point of inflection requires a change in concavity, which is strictly a change in the sign of the second derivative. This makes concavity analysis central to locating inflection points.

While a second derivative equal to zero or undefined is necessary for an inflection point, it is not sufficient. The crucial criterion is the actual sign change of $f''(x)$ as the graph passes through the point. Thus, a strong conceptual understanding involves more than solving an equation; it requires analyzing function behavior around candidate values.

A function’s graph must also be defined near the point being considered. Even if the second derivative changes sign, if the function is not defined at or near that value—for example, at discontinuities or vertical asymptotes—the point cannot be an inflection point.

How to Determine Whether a Point Is an Inflection Point

Because concavity changes describe shifts in the bending of the graph, a careful, stepwise approach helps confirm the presence of an inflection point. Although these notes do not include worked examples, the conceptual process is essential for AP-level mastery.

Conceptual Steps

Students should understand the following overall structure when determining whether a point is truly a point of inflection:

• Check that the function is defined near the candidate point. A function must exist in an open interval around the point for concavity to be meaningful.
• Find where the second derivative is zero or does not exist. These x-values are candidates for inflection points because the concavity might change there.
• Determine the sign of the second derivative on intervals around the candidate. Concavity is interpreted through the sign of $f''(x)$, so this check is essential.
• Confirm that the sign of $f''(x)$ actually changes. A switch from positive to negative or negative to positive establishes a true inflection point.
• Relate concavity behavior back to graph shape. Understanding how the graph bends around the point reinforces conceptual clarity.

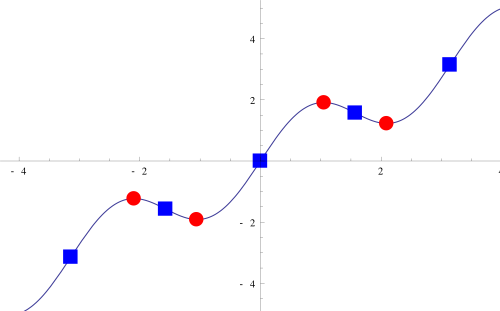
A graph of $f(x) = x + \sin(2x)$ showing stationary points as red circles and inflection points as blue squares. The plotted curve illustrates where concavity changes occur along the function, highlighting the distinction between inflection points and local extrema. This image includes extra detail about stationary points and a trigonometric function but remains aligned with the conceptual contrast needed for this topic. Source.

Geometric and Graphical Interpretation

From a geometric standpoint, a point of inflection marks a shift in the “shape” of the curve. In a concave-up region, the graph bends upward and the slope of the tangent line increases. In a concave-down region, the graph bends downward and tangent slopes decrease. Where these tendencies reverse, the curve adjusts its bending direction, producing the signature behavior associated with inflection points.

Why Inflection Points Matter

Inflection points play a major role in understanding a function’s structure and behavior:

• They indicate changes in how rapidly a function is increasing or decreasing.
• They help describe the overall shape of the function, an essential skill for sketching graphs.
• They provide insight into related rates of change through connections between $f$, $f'$, and $f''$.
• They reflect subtle, meaningful transitions where curvature shifts, deepening understanding of the function’s growth patterns.

In AP Calculus AB, defining and recognizing inflection points ensures that students can analyze curves comprehensively, moving beyond simple increases and decreases to interpret how functions bend and evolve across intervals.