AP Syllabus focus:
‘Construct left and right Riemann sums by multiplying function values at subinterval endpoints by subinterval widths to approximate a definite integral.’
Left and right Riemann sums provide foundational ways to approximate definite integrals by multiplying strategic function values with subinterval widths across a selected partition of the domain.
Understanding Left and Right Riemann Sums
Left and right Riemann sums are numerical approximation techniques that estimate accumulated change by breaking an interval into smaller pieces and using the function’s values at specific endpoints. These approximations allow students to connect discrete calculations to the meaning of a definite integral as the total accumulated change represented by area under a curve.
When constructing these approximations, it is essential to identify the partition, the set of points dividing the interval, and the sample points, which in this context are the left or right endpoints of each subinterval.
Partitioning an Interval
A partition divides the interval into smaller subintervals. These subintervals may be uniform or nonuniform, but for this subsubtopic, the focus is on using subinterval endpoints in constructing sums. Once the interval is divided, each subinterval’s width provides the basis for multiplying by the function’s sampled value.
Subinterval: A smaller interval created by partitioning a larger interval into consecutive pieces used for constructing a Riemann sum.
After identifying subintervals, the width of each segment becomes the multiplier for the function value at either the left or right endpoint.
Subinterval Width
For uniform partitions, all subinterval widths are equal, and this consistent spacing simplifies the structure of the sums. When widths are constant, the pattern within the Riemann sum becomes clearer and more directly connected to integral notation.
= Width of each subinterval in a uniform partition
= Number of subintervals
The value of plays a key role in determining how the approximation behaves as the number of subintervals increases.
Constructing a Left Riemann Sum
Using Left Endpoints
A left Riemann sum approximates the area under a curve by taking the value of the function at the left endpoint of each subinterval. This approach uses earlier information within the interval to estimate the accumulation across each piece.
Left Riemann Sum: An approximation of an integral obtained by evaluating the function at the left endpoint of each subinterval, then multiplying by subinterval width.
Because each rectangle’s height is determined before the curve changes across the subinterval, the accuracy of the approximation depends strongly on whether the function is increasing or decreasing in that region. Nevertheless, this method offers a systematic and structurally consistent way to construct approximations.
Structure of the Left Sum
A left Riemann sum includes one term per subinterval, and each term is formed by multiplying a function value by .
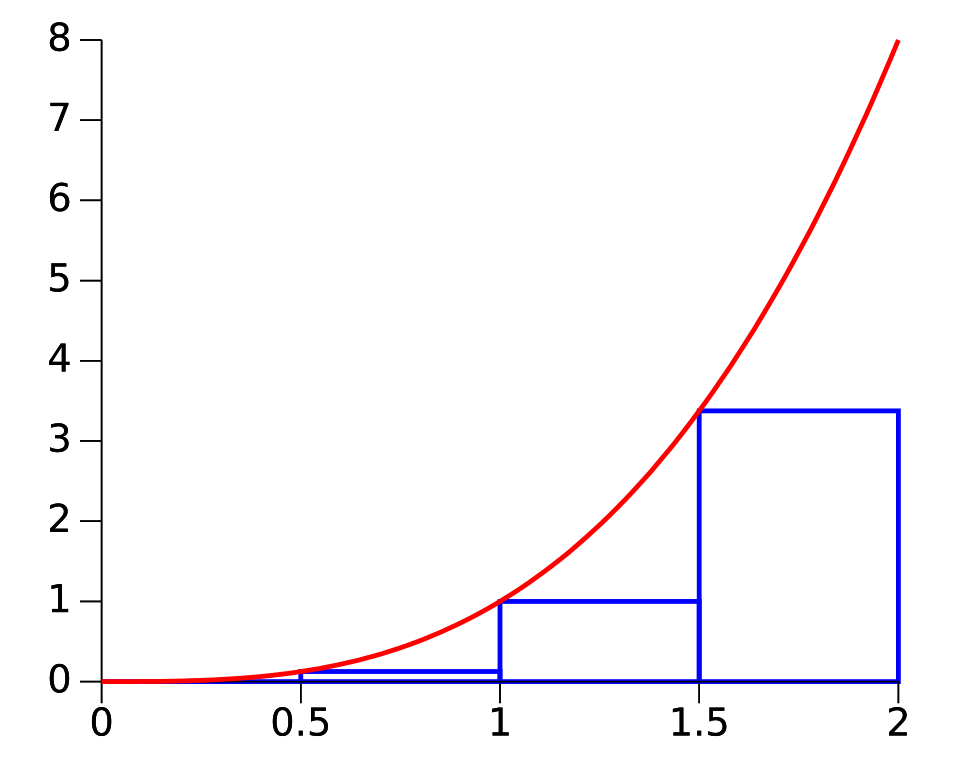
This diagram illustrates a left Riemann sum for on the interval using four equally spaced subintervals. The height of each rectangle is determined by the function value at the left endpoint. It visually demonstrates how left-endpoint sampling builds an approximation of the definite integral. Source.
The height of each rectangle directly reflects the function’s behavior at the left point of the subinterval.
Important characteristics:
Uses the first point of each subinterval
Provides a consistent pattern for summation
Often aligns with real-world scenarios where initial rates define change
Constructing a Right Riemann Sum
Using Right Endpoints
A right Riemann sum uses the right endpoint of each subinterval to estimate the function’s behavior across that interval. This positioning incorporates information at the end of each subinterval and produces a different approximation pattern from the left sum.
Right Riemann Sum: An approximation of an integral obtained by evaluating the function at the right endpoint of each subinterval, then multiplying by subinterval width.
The right endpoint captures the function value after any changes occurring across the subinterval. This reflects how accumulated change might be estimated when the rate at the end of an interval is more representative of the quantity’s overall behavior.
Structure of the Right Sum
A right Riemann sum uses the right endpoint of each subinterval to estimate the function’s behavior across that interval.
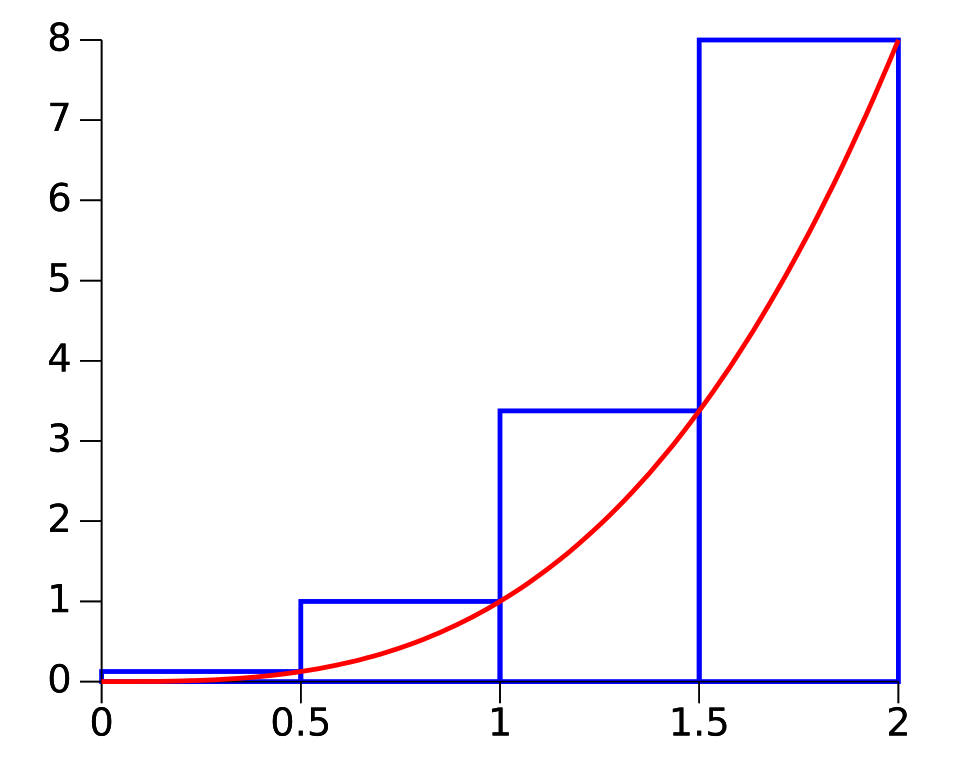
This diagram shows a right Riemann sum for on using four equal subintervals. Each rectangle’s height is set by the value of the function at the right endpoint. It demonstrates how right-endpoint sampling changes the approximation relative to left-endpoint methods. Source.
The right endpoint typically produces rectangles that capture later changes in the function.
Key characteristics:
Uses the final point within each subinterval
Produces a consistent sequence of multiplications
Provides distinct behavior for functions that are not constant
Conceptual Significance
Understanding How These Sums Approximate Accumulated Change
Left and right Riemann sums help students build intuition for definite integrals by illustrating how accumulation emerges from adding products of rates and widths. Each rectangle approximates a slice of total change, and adding them reveals how integration generalizes the process to infinitely many slices.
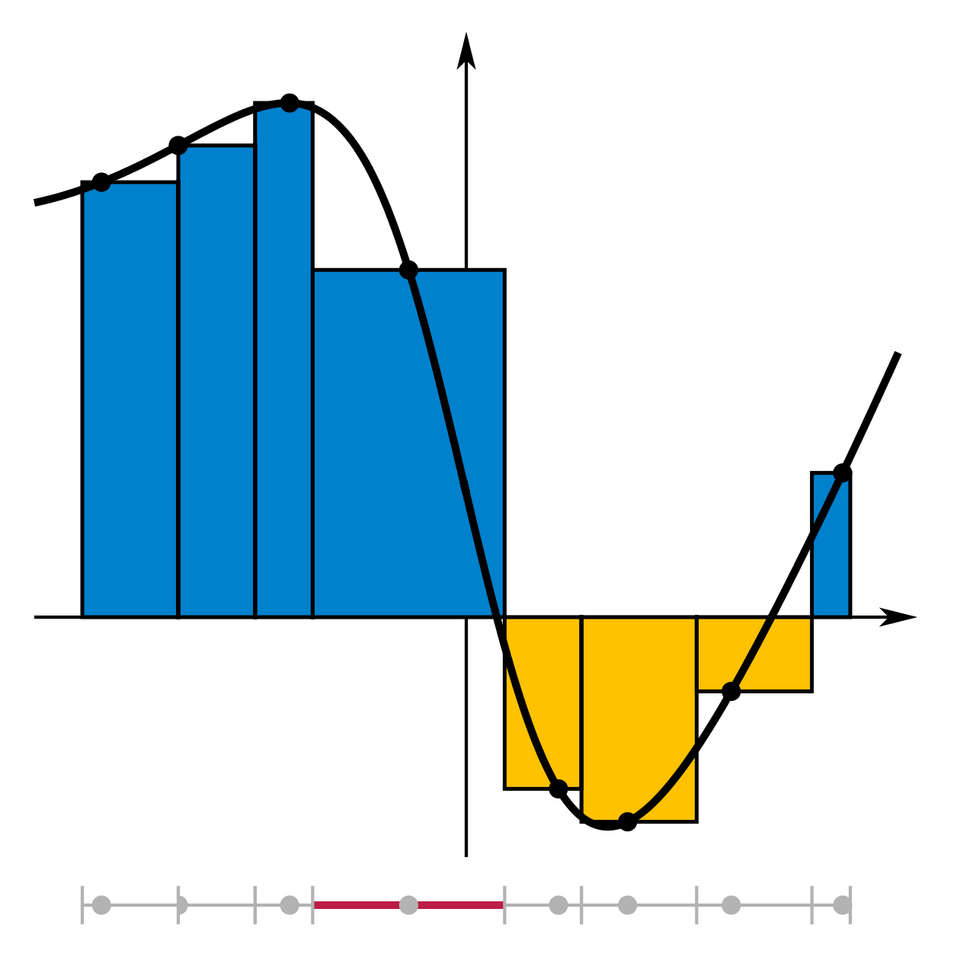
This graph depicts a Riemann sum using rectangles of possibly unequal widths beneath a smooth curve. The tops of the rectangles meet the curve at chosen sample points, illustrating how sums of rectangle areas approximate a definite integral. Extra detail: the irregular partition and complex function extend beyond AP Calculus AB expectations but still show the core concept effectively. Source.
Using Riemann Sums to Connect Discrete and Continuous Ideas
These sums show how finite approximations evolve toward exact values as intervals become finer. The method of selecting endpoints highlights the relationship between interval sampling and resulting approximation. For functions that are smooth, increasing the number of subintervals provides a closer estimation of the true integral, reinforcing the connection between Riemann sums and integration.
FAQ
Increasing the number of subintervals generally improves accuracy because each rectangle better conforms to the local behaviour of the function.
With narrower subintervals, the difference between left and right endpoint values decreases, reducing the overestimate or underestimate associated with monotonic functions.
For highly curved functions, increasing subintervals especially reduces distortion introduced by steep changes.
Only when the function is strictly increasing or strictly decreasing on the interval.
• For increasing functions: left sums underestimate and right sums overestimate.
• For decreasing functions: left sums overestimate and right sums underestimate.
If the function changes direction within the interval, neither sum consistently overestimates nor underestimates.
Yes. The definitions do not require equal-width subintervals.
However, different widths complicate the sum because each rectangle must be multiplied by its corresponding distinct width.
This approach is useful when data points are irregularly spaced, such as measurements taken at unequal time intervals.
A left or right Riemann sum can still be computed, but accuracy decreases if the discontinuity is large.
Jump discontinuities create abrupt changes in rectangle height, and the approximation may poorly represent the actual area.
For removable discontinuities, the method remains largely unaffected because the missing point does not prevent evaluating nearby endpoint values.
They provide the conceptual foundation for understanding how definite integrals arise from approximating accumulation.
Endpoint selection creates a structured way to link discrete sums with the continuous concept of integration.
More advanced approximations, such as trapezoidal or midpoint methods, build directly on the logic introduced by left and right Riemann sums.
Practice Questions
Question 1 (1–3 marks)
A function f is increasing and continuous on the interval [2, 5]. The interval is divided into four equal subintervals.
Explain whether the left Riemann sum or the right Riemann sum will give a larger approximation for the integral from 2 to 5 of f(x) dx.
Question 1 (1–3 marks)
• 1 mark for identifying that the right Riemann sum gives a larger approximation.
• 1 mark for stating that the function is increasing on the interval.
• 1 mark for explaining that for an increasing function, right endpoint values are larger than left endpoint values on each subinterval, so the right sum overestimates relative to the left.
Question 2 (4–6 marks)
A continuous function g is defined on the interval [0, 8]. The table below gives values of g at selected points:
x: 0, 2, 4, 6, 8
g(x): 5, 3, 4, 7, 6
The interval [0, 8] is divided into four subintervals of equal width.
(a) Use a left Riemann sum to approximate the integral from 0 to 8 of g(x) dx.
(b) Use a right Riemann sum to approximate the same integral.
(c) Given that g is decreasing on [0, 2] and increasing on [2, 8], determine which of your two answers is likely to be closer to the true value of the integral, and explain why.
Question 2 (4–6 marks)
(a) Left Riemann sum (2 marks total)
• 1 mark for using the function values at x = 0, 2, 4, and 6.
• 1 mark for multiplying each by the subinterval width (which is 2) and summing to obtain 2(5 + 3 + 4 + 7) = 38.
(b) Right Riemann sum (2 marks total)
• 1 mark for using the function values at x = 2, 4, 6, and 8.
• 1 mark for multiplying each by the subinterval width 2 and summing to obtain 2(3 + 4 + 7 + 6) = 40.
(c) Explanation of which is closer (2 marks total)
• 1 mark for stating that the right Riemann sum is likely closer.
• 1 mark for explaining that the function decreases at first then increases, so the left sum uses the larger initial value (5) for the first subinterval causing an overestimate, while the right sum uses the smaller value (3) on that subinterval.

