Midpoint and trapezoidal approximations provide structured numerical methods for estimating definite integrals when analytic integration is difficult, impossible, or unnecessary, supporting deeper understanding of accumulated change.

Midpoint and Trapezoidal Approximations

Midpoint and trapezoidal methods are two major numerical strategies for approximating definite integrals using Riemann sums. Each method replaces the exact area under a curve with shapes whose areas can be computed more easily. These approaches apply whether an interval is divided into uniform partitions (all subintervals equal width) or nonuniform partitions (varying widths).

Understanding the Purpose of Numerical Integration

Numerical integration is used to approximate the value of $\int_a^b f(x),dx$ when the function is known only through graphs, tables, or difficult expressions. Midpoint and trapezoidal sums interpret accumulation through geometric estimation, connecting rate functions to total change.

Midpoint Riemann Sums

The midpoint Riemann sum estimates the area under a curve by using the height of the function at the midpoint of each subinterval. For each subinterval, the method constructs a rectangle whose width matches the subinterval width and whose height equals the function’s value at the midpoint.

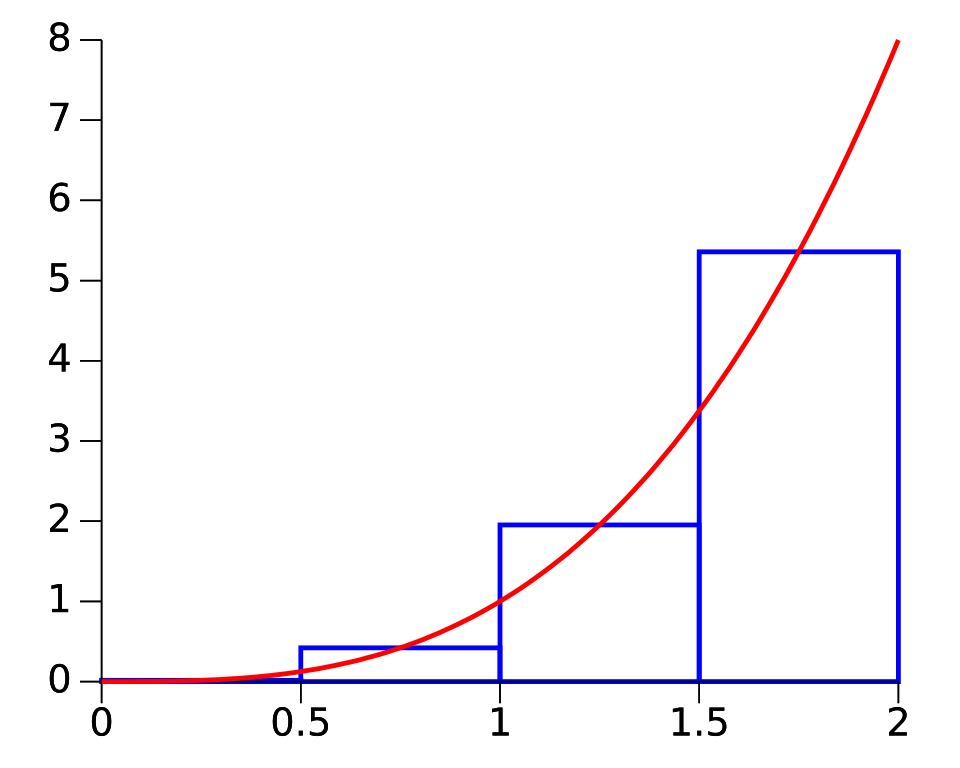
This graph illustrates a midpoint Riemann sum for a function using four subintervals on $[0,2]$, with each rectangle’s height determined by the function value at its midpoint. The diagram visually represents how midpoint sampling approximates $\int_a^b f(x),dx$. The specific function shown, $f(x)=x^3$, adds concrete context without introducing concepts beyond the syllabus. Source.

Because midpoints tend to balance portions where the function is increasing or decreasing, the midpoint method often provides a more accurate estimate than basic left or right Riemann sums.

Choosing Midpoints

Each midpoint must lie strictly inside its subinterval. For uniform partitions, midpoints follow a predictable pattern, while for nonuniform partitions, each midpoint must be identified separately.

Features of the Midpoint Approach

• Uses rectangles as approximating shapes.

• Height determined at midpoints rather than endpoints.

• Often gives improved accuracy for functions with symmetric behavior on subintervals.

• Works for both uniform and nonuniform partitions.

Trapezoidal Approximations

The trapezoidal sum replaces the curved region with trapezoids rather than rectangles.

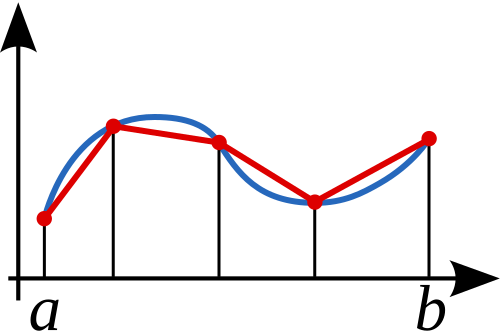
This illustration shows the composite trapezoidal rule applied to approximate $\int_a^b f(x),dx$. Trapezoids are formed using endpoint function values as parallel sides, demonstrating how the method approximates area across uniform subintervals. The graphic exemplifies the trapezoidal method emphasized in the syllabus. Source.

This method averages the left and right endpoint heights, producing an estimate that tends to correct overestimates and underestimates common to simple endpoint-based Riemann sums.

Shape Interpretation

Because the top edge of each trapezoid slants between the two endpoint function values, the trapezoidal method more closely follows curves that change gradually across each subinterval.

Features of the Trapezoidal Method

• Uses trapezoids instead of rectangles.

• Incorporates both left and right endpoint values.

• Provides improved accuracy for functions that are approximately linear on subintervals.

• Functions smoothly for uniform and nonuniform partitions.

Uniform vs. Nonuniform Partitions in Approximations

Both midpoint and trapezoidal approaches remain valid regardless of partition type. However, the computational structure differs because widths may vary.

Uniform Partitions

In a uniform partition, the interval $[a, b]$ is divided into $n$ subintervals of equal width. This allows consistent use of a single width value and simplifies midpoint identification.

Uniform partitions typically streamline approximation because patterns in midpoints and endpoints repeat predictably across subintervals.

Nonuniform Partitions

A nonuniform partition divides the interval into subintervals of different widths. Midpoint and trapezoidal sums must be computed individually for each subinterval:

• Each subinterval receives its own width.

• Each midpoint must be located accurately.

• Function values must be evaluated at each relevant point rather than following a repeated pattern.

Nonuniform partitions are essential when data come from tables or real-world measurements that do not occur at evenly spaced inputs.

Constructing Midpoint and Trapezoidal Approximations

Both methods follow structured processes that guide students toward accurate numerical results.

Midpoint Approximation Process

• Partition the interval into subintervals (uniform or nonuniform).

• Identify the midpoint of each subinterval.

• Evaluate the function at each midpoint.

• Multiply each midpoint value by the width of its subinterval.

• Add all resulting products to approximate the integral.

Trapezoidal Approximation Process

• Partition the interval into subintervals.

• Evaluate the function at each endpoint of each subinterval.

• For each subinterval, compute the average of the two endpoint values.

• Multiply each average by the corresponding subinterval width.

• Sum all contributions to estimate the integral.

Accuracy Considerations

Midpoint and trapezoidal approximations reduce but do not eliminate error. Their effectiveness depends on:

• The curvature of the function within each subinterval.

• Whether subintervals are narrow and numerous.

• Whether a function is smooth or changes abruptly.

Midpoint sums often outperform trapezoidal sums for functions with curvature symmetric around midpoints, whereas trapezoidal sums are effective for nearly linear behavior on subintervals.

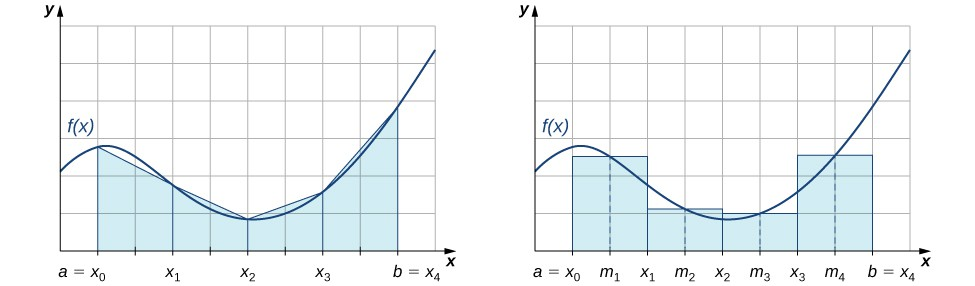
This paired diagram compares how the trapezoidal rule and midpoint rule approximate $\int_a^b f(x),dx$. The upper graph uses trapezoids formed from endpoint values, while the lower graph uses rectangles whose heights come from midpoints, highlighting methodological differences. The figure includes commentary on relative accuracy, which extends slightly beyond the AP AB syllabus but reinforces conceptual distinctions discussed in the notes. Source.