AP Syllabus focus:
‘Use technology, when appropriate, to compute numerical approximations for definite integrals and interpret the results in context.’
Technology-based numerical integration allows students to evaluate definite integrals when analytical methods are difficult or impossible, supporting accurate approximations and contextual understanding in applied problems.
Using Technology to Approximate Definite Integrals
Technology is often used to approximate definite integrals when a function is too complicated to integrate symbolically or when only discrete data are available. In AP Calculus AB, this typically involves graphing calculators or digital computation tools capable of numerically evaluating integrals. These tools implement established numerical algorithms internally, allowing students to focus on interpreting results, selecting appropriate methods, and understanding how approximations reflect accumulated change.

Front view of a TI-83 Premium CE graphing calculator, illustrating the type of tool commonly used for numerical integration. Students input functions and bounds on similar devices to compute approximate values of definite integrals. The physical detail shown exceeds typical syllabus needs but accurately reflects referenced technology. Source.
Understanding What Technology Computes
Most handheld and digital tools approximate using methods such as adaptive numerical integration, where the tool increases accuracy by refining subintervals. Even though the internal algorithms vary, the essential idea is that the technology estimates area under a curve by sampling the function at many points.
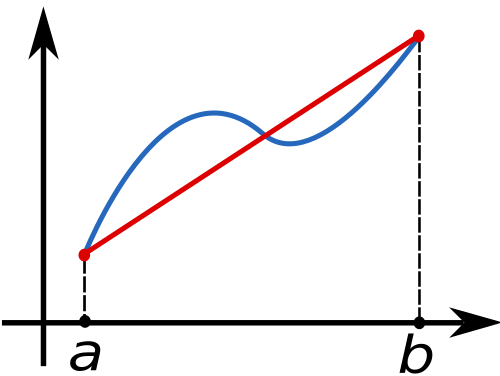
Illustration of the trapezoidal rule for numerical integration, showing how a curved region is approximated using trapezoids. This mirrors the principle embedded in technological integration algorithms. The diagram includes more geometric detail than the syllabus explicitly requires but remains directly supportive of the concept. Source.
Because students must interpret output in context, understanding what is being approximated—the total accumulated change of a quantity—is crucial.
To support this interpretation, students need clarity on the underlying meaning of definite integral. A definite integral represents the accumulated net change of a quantity, measured through the signed area under the function's graph.
Accumulated Change: The net amount by which a quantity increases or decreases over an interval, found by totaling the signed area under its rate-of-change function.
Using technology enhances accuracy and efficiency, but students must still link the computed value to the behavior of the original function.
A key idea in technology-assisted integration is that the calculator uses a numerical estimate. Even though students do not need to know the algorithmic details, they must recognize that the output is an approximation, not an exact symbolic antiderivative.
= Definite integral representing accumulated change over
= Rate of change of the quantity (units vary by context)
= Bounds representing start and end values of the independent variable
It is important for students to observe that the calculator’s output depends on correct entry of bounds and functions, reinforcing careful attention to notation.
Appropriate Use of Technology
AP Calculus AB expects students to know when technology should be employed. Technology is appropriate when:
The integrand has no elementary antiderivative, making symbolic integration challenging.
The integrand is given numerically or graphically, without an explicit formula.
A quick estimate is needed to confirm or compare with a manually generated Riemann sum.
The problem context requires a numerical value rather than symbolic manipulation.
Technology should not replace conceptual understanding. Instead, it supports interpretation by ensuring accurate approximations when manual computation is impractical.
Technology Entry and Setup
To use technology effectively, students must understand the steps required to evaluate a definite integral numerically.
Common steps include:
Entering the function into the calculator or digital tool accurately.
Specifying the correct interval for accumulation.
Using an integral-evaluation command (such as a calculator’s “fnInt” or graphical integration feature).
Confirming that the window or viewing settings clearly show the region under consideration.
Interpreting the numerical result with proper units from the context.
Even though tools handle the computation, students must supervise the process to ensure the output reflects the actual mathematical question.
Interpreting Numerical Output
Interpreting approximate integral values is essential for full credit on AP free-response questions. Students must describe what the number means in the real-world situation and clarify whether it represents net change, total increase, or accumulated quantity.
Important interpretive considerations include:
Units: The integral’s units equal (units of rate) × (units of the independent variable), ensuring the answer reflects a meaningful physical or contextual quantity.
Sign: A positive integral indicates net increase; a negative integral indicates net decrease.
Magnitude: Larger absolute values represent greater overall change across the interval.
Contextual phrasing: Answers must translate the numerical value into a statement about the situation, such as “the population increased by approximately…” or “the water level decreased by…”.
Students should recognize that technology outputs support reasoning rather than replace it.
Connecting Technology to Numerical Methods
Although the calculator automates integration, its approximations relate directly to Riemann sums, midpoint approximations, and trapezoidal sums introduced earlier in the course. Understanding this connection helps students recognize why technological integration produces reasonable numerical answers.
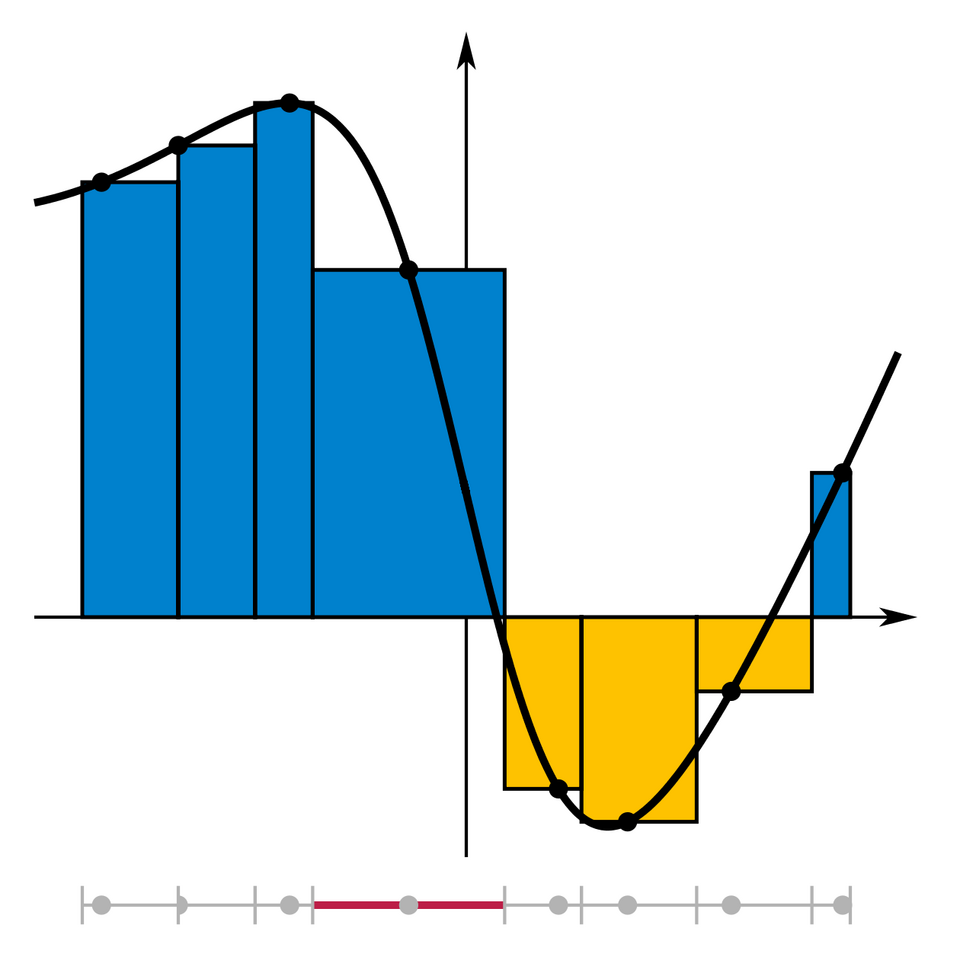
Example of a Riemann sum approximation, illustrating how rectangular areas approximate accumulated change. The visual demonstrates how numerical tools sample function values across subintervals. The highlighted irregular interval adds detail beyond syllabus requirements but supports conceptual understanding. Source.
Key connections include:
Technology uses sampling of function values over many small subintervals.
Smaller subinterval width improves approximation accuracy, similar to refining a Riemann sum.
The integral approximation represents net signed area, combining positive and negative contributions.
Because AP Calculus emphasizes conceptual understanding, students must appreciate how technology-based results reflect the same foundational ideas behind manually computed numerical methods.
Limitations and Careful Use
While technology provides powerful tools, students must remain aware of limitations:
Incorrect window settings can mislead interpretation of the graph.
Mistyping bounds or functions yields incorrect values.
Integrals with steep behavior or rapid oscillation may require closer inspection to ensure the approximation is meaningful.
Technology cannot determine symbolic antiderivatives; it only approximates numerical values.
Recognizing these limitations strengthens mathematical judgment and ensures proper use of computational tools in solving definite integrals.
FAQ
Calculator algorithms are generally far more accurate because they adapt the number and size of subintervals based on the behaviour of the function.
Manual Riemann sums use fixed intervals, so their accuracy depends strongly on the chosen partition.
In contrast, calculator methods refine intervals where the function changes rapidly, giving more reliable approximations without user intervention.
Yes. Most numerical integration tools compute the net signed area automatically, adding positive contributions and subtracting negative ones.
However, the user must still interpret whether the context requires net change or total magnitude, as calculators do not distinguish between these interpretations by default.
Different brands and models use different numerical integration algorithms. Some rely on adaptive trapezoidal methods, while others use Simpson-type techniques.
These variations lead to small differences, especially when the function is highly oscillatory or has rapid curvature changes.
Accuracy issues most commonly arise when a function:
• oscillates rapidly
• has sharp turns or corners
• changes steeply over very small intervals
Such features can force the calculator to approximate complex behaviour with overly large intervals, reducing precision.
Yes. If divergence occurs near an endpoint and the calculator samples points that avoid the problematic region, it may still return a finite number.
Because technology does not analyse divergence, users must recognise when a function is unbounded or when the interval is inappropriate, even if a numerical output is provided.
Practice Questions
(1–3 marks)
A function R represents the rate, in litres per minute, at which water flows into a tank. The graph of R is shown on a calculator screen, and the calculator reports that the numerical value of the definite integral of R from t = 0 to t = 6 is approximately 42.3.
State the meaning of 42.3 in the context of the problem.
Question 1 (1–3 marks)
• 1 mark: Identifies that 42.3 represents an accumulated amount.
• 1 mark: States that it is the total volume of water added to the tank over the 6 minutes.
• 1 mark: Includes correct units (litres or litres per minute times minutes).
(4–6 marks)
A function v(t) gives the velocity, in metres per second, of a particle moving along a line for 0 ≤ t ≤ 8. The function is complicated and does not have an elementary antiderivative. A student uses a calculator to evaluate the integral of v(t) from t = 0 to t = 8 and obtains an approximate value of 17.6.
(a) Explain why using a calculator is appropriate in this situation.
(b) Interpret the value 17.6 in terms of the motion of the particle.
(c) The student claims that the answer must be an underestimate. Give a valid reason why this claim might be incorrect.
Question 2 (4–6 marks)
(a) (1–2 marks)
• 1 mark: States that the function has no simple antiderivative or is too complicated to integrate by hand.
• 1 mark: Notes that technology is appropriate for obtaining a numerical approximation.
(b) (1–2 marks)
• 1 mark: Identifies that 17.6 represents the net displacement of the particle over the interval.
• 1 mark: Uses correct units (metres) and describes it as the total change in position from t = 0 to t = 8.
(c) (1–2 marks)
• 1 mark: States that the approximation could be an overestimate depending on the behaviour of the function (for example, the function might be decreasing or have concavity that leads to overestimation).
• 1 mark: Gives a clear mathematical justification, such as noting that the calculator may use a method like the trapezoidal rule, which does not always underestimate.

