This section explains how verifying a general solution by differentiation ensures that the separated and integrated expression truly satisfies the original differential equation for all allowable values.

Verifying General Solutions by Differentiation

To verify a general solution means to demonstrate that a function obtained through separation of variables actually satisfies the original differential equation. After solving a separable differential equation, students compute its derivative and confirm that the resulting expression matches the derivative relationship given in the differential equation. This verification step reinforces the logical connection between solution formulas and the differential equations from which they are derived.

Understanding the Purpose of Verification

When separation of variables is used to solve a differential equation, the integration process produces a family of general solutions that include an arbitrary constant. Because integration may introduce algebraic manipulations that obscure the relationship between $y$ and $dy/dx$, it is essential to confirm that the derived expression actually works. Verification ensures that:

• The general solution satisfies the differential equation for every permissible value of the constant.

• No steps in the separation or integration process have introduced extraneous expressions.

• The function behaves consistently with the structure and meaning of the original rate relationship.

This graph displays a family of solution curves for a first-order differential equation, with each curve corresponding to a different value of the arbitrary constant. The curves collectively illustrate how a general solution represents infinitely many functions that all satisfy the same differential equation. The image includes additional visual variety not required by the syllabus but remains directly relevant to the concept of general solution families. Source.

Verification based on differentiation shows that these family members are not just theoretical expressions but actual functions that satisfy the given differential equation for all appropriate values.

Differentiation as a Verification Tool

Differentiation is central to the verification process because differential equations describe how a function changes. When verifying, students compute the derivative of the proposed general solution and then substitute both the function and the derivative into the differential equation to test whether the equality holds. The differential equation dictates a specific pattern of change, and verification checks whether the proposed general solution displays exactly that pattern.

Before substituting, students must compute a correct derivative and express it in a form compatible with the differential equation’s structure. This ensures that substitution is meaningful and directly comparable to the relationship the equation describes.

Structure of the Verification Process

Students benefit from approaching verification with a consistent set of steps. A structured method helps prevent errors and supports clear mathematical reasoning. This procedure highlights how the derivative and the original function work together to satisfy the differential equation.

Core Steps in Verifying a General Solution

• Identify the original differential equation and the proposed general solution.

• Differentiate the proposed general solution carefully with respect to the appropriate independent variable.

• Substitute both the function and its derivative into the differential equation.

• Simplify the resulting expression to confirm the equality holds for all values in the domain of the solution.

• Conclude that the function is verified as a general solution if the original equation is satisfied identically.

These steps reinforce the connection between algebraic expressions obtained through integration and the original rate relationship specified in words or symbolic notation.

The Role of Algebraic Rearrangement

Because solutions found through separation of variables may not immediately resemble the form of the original differential equation, algebraic manipulation plays an important role in verification. Students must be able to:

• Rewrite expressions involving exponentials, logarithms, or powers as needed.

• Express the derivative in a way that aligns with the structure of the differential equation.

• Recognize equivalent forms of mathematical expressions even when they look different from the original equation.

This reinforces the mathematical flexibility expected in calculus and ensures students understand the underlying rate relationships rather than relying solely on memorized forms.

Equations and Functional Relationships

Verification often involves expressing relationships in symbolic form. When appropriate, a differential equation can be represented as an explicit equality demonstrating how the derivative depends on the function.

This symbolic representation highlights the relationship that the general solution must satisfy. Verification demonstrates that substituting the function and its derivative into this formal expression yields an identity.

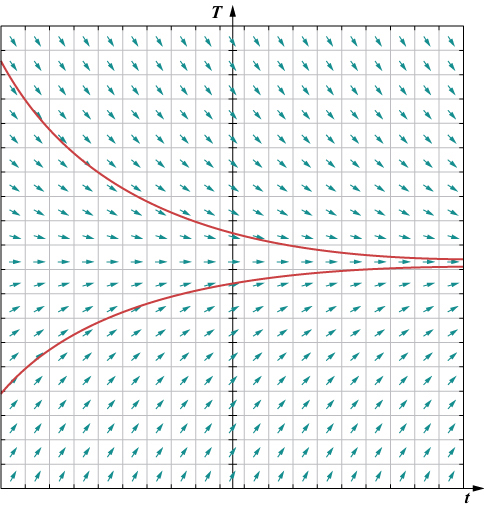
This direction field for the differential equation $T'(t) = -0.4(T - 72)$ illustrates how each small line segment shows the slope prescribed by the differential equation at that point. The solution curves follow these slopes, demonstrating how a true solution must match the differential equation’s slope behavior everywhere. The real-world cooling context is beyond the syllabus but effectively visualizes slope-based verification. Source.

A sentence continues the explanation: Verification ensures that the derived solution retains the relationship prescribed by the model in both its structure and behavior.

Importance of Domain Awareness

Verification implicitly requires the student to consider where the solution is defined. Because solving by separation often introduces logarithmic or fractional expressions, domain restrictions may arise that need to be acknowledged when checking the solution. A function cannot satisfy a differential equation outside its domain, and verification must reflect this limitation.

Connecting Verification to Conceptual Understanding

Verifying general solutions strengthens conceptual understanding of differential equations by reinforcing the idea that solving is not merely a mechanical process. It emphasizes:

• The logical flow from differential equation to separated form to integrated expression.

• The critical role of derivatives in expressing change.

• The distinction between finding a solution and proving that it works.

This subsubtopic ensures that students can confirm the correctness of general solutions obtained using separation of variables, aligning with the syllabus expectation that they show how differentiation validates the relationship between a function and its derivative.