Exponential differential equations appear frequently in real-world modeling, linking changing quantities to growth or decay patterns. This subsubtopic develops the skill of translating contextual descriptions into differential equations.

Understanding Verbal Descriptions that Indicate Exponential Change

When interpreting verbal statements, AP Calculus AB students must recognize when a situation implies exponential growth or exponential decay. A typical description signals that a quantity changes at a rate tied directly to its current amount. This relationship reveals important structure in the underlying differential equation.

A common verbal cue is the phrase “rate of change is proportional to the quantity itself.” The word proportional indicates that the derivative is a constant multiple of the current value of the dependent variable. Because proportionality is central to exponential modeling, it is essential to articulate precisely what the phrase communicates mathematically.

Such proportional descriptions appear across many contexts—population growth, radioactive decay, and other processes where change accelerates or slows depending on current levels.

This graph shows an exponentially increasing population $N$ over time $t$, illustrating the qualitative behavior associated with differential equations of the form $\frac{dN}{dt}=kN$ when k>0. As time passes, the curve steepens, reflecting how the rate of change increases when the quantity itself is larger. The axis labels are in Portuguese, but the mathematical behavior remains fully aligned with AP Calculus AB exponential growth models. Source.

Identifying Dependent and Independent Variables from Context

Before writing a differential equation, students must determine which quantity depends on another. In exponential models, the dependent variable typically represents the evolving quantity, while the independent variable generally represents time.

To interpret a verbal statement effectively, identify:

• What quantity is changing.

• What variable describes the passage of time or another driving factor.

• How the rate of change relates to the current state of the quantity.

Once this structure is clear, the appropriate symbolic notation follows naturally. Students then express the derivative of the dependent variable with respect to the independent variable and match it to the described proportional behavior.

Translating Proportional Change into Derivative Notation

Verbal descriptions often use everyday language rather than mathematical terminology. To move from English sentences to mathematical form, students must recognize the equivalent symbolic expressions.

Key phrases that typically correspond to exponential differential equations include:

• “Rate of change is proportional to the amount present.”

• “Changes at a rate directly proportional to its size.”

• “Decreases at a rate proportional to the current value.”

• “Increases at a rate proportional to the quantity.”

Each of these statements implies that the derivative equals a constant multiplied by the function itself. The constant may represent a growth rate (positive) or decay rate (negative).

This differential equation expresses the essential meaning of proportional change: the slope of the solution curve at any time depends on the value of the function at that moment. After forming this equation, the rest of the analysis—solving or interpreting—relies entirely on the model expressed.

A sentence such as “the amount of a substance decreases at a rate proportional to its mass” would therefore lead directly to the same differential equation form, although with k < 0. The sign of the constant determines whether the process represents growth or decay.

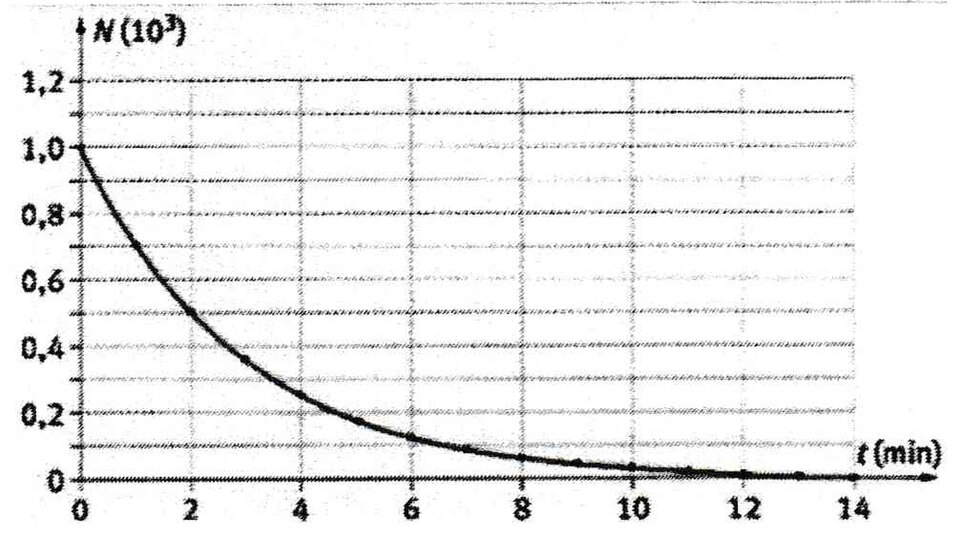
This figure displays an exponentially decreasing quantity $N(t)$ over time, characteristic of a decay model such as $\frac{dN}{dt}=kN$ with k<0. The curve drops steeply at first and then gradually levels toward zero, highlighting that the magnitude of the rate of change is greatest when more material is present. The half-life markings offer extra detail beyond the AP syllabus, but remain consistent with the core idea of exponential decay in differential equation modeling. Source.

Distinguishing Growth and Decay from Verbal Indicators

The presence of the word increases or grows usually signals exponential growth, implying a positive proportionality constant. Conversely, wording such as decreases, decays, or diminishes typically indicates exponential decay, where the proportionality constant is negative.

Students should evaluate:

• Whether the context implies continual increase.

• Whether the context highlights gradual decline.

• Whether the magnitude of change depends on current size.

These cues ensure accurate translation of the statement into mathematical form. Although the same symbolic structure appears, recognizing the correct sign of the proportionality constant is crucial for representing the intended behavior.

Interpreting the Meaning of the Exponential Differential Equation in Context

Once a differential equation of the form $\frac{dy}{dt} = ky$ is written, students must understand what the expression communicates about the modeled phenomenon. This includes interpreting each component of the equation:

• $\frac{dy}{dt}$ describes the instantaneous rate of change of the quantity.

• $y$ represents the current state or amount.

• $k$ encodes how strongly the rate responds to the current amount.

The model asserts that the system’s behavior is governed entirely by this dependence: the larger the quantity becomes, the faster it grows or decays (in magnitude). This relationship captures many natural and human processes in a concise mathematical expression.

Recognizing these features strengthens students’ ability to connect symbolic differential equations with real-world descriptions. The differential equation serves as a bridge between contextual language and the mathematical representation essential for further analysis.