This subsubtopic focuses on solving first-order exponential differential equations of the form $\frac{dy}{dt} = ky$, showing how separation of variables leads naturally to the exponential solution model.

Solving the Differential Equation $\frac{dy}{dt} = ky$

The differential equation $\frac{dy}{dt} = ky$ represents a relationship in which the rate of change of a quantity is directly proportional to the amount present. This structure appears frequently in natural and applied settings such as population growth, radioactive decay, and interest accumulation, making it essential for AP Calculus AB students to understand how to solve it analytically.

When a differential equation expresses a derivative in terms of the dependent variable multiplied by a constant, it is known as an exponential differential equation, introduced when the equation takes the form $\frac{dy}{dt} = ky$. The constant k determines the growth or decay behavior and remains central throughout the solution process.

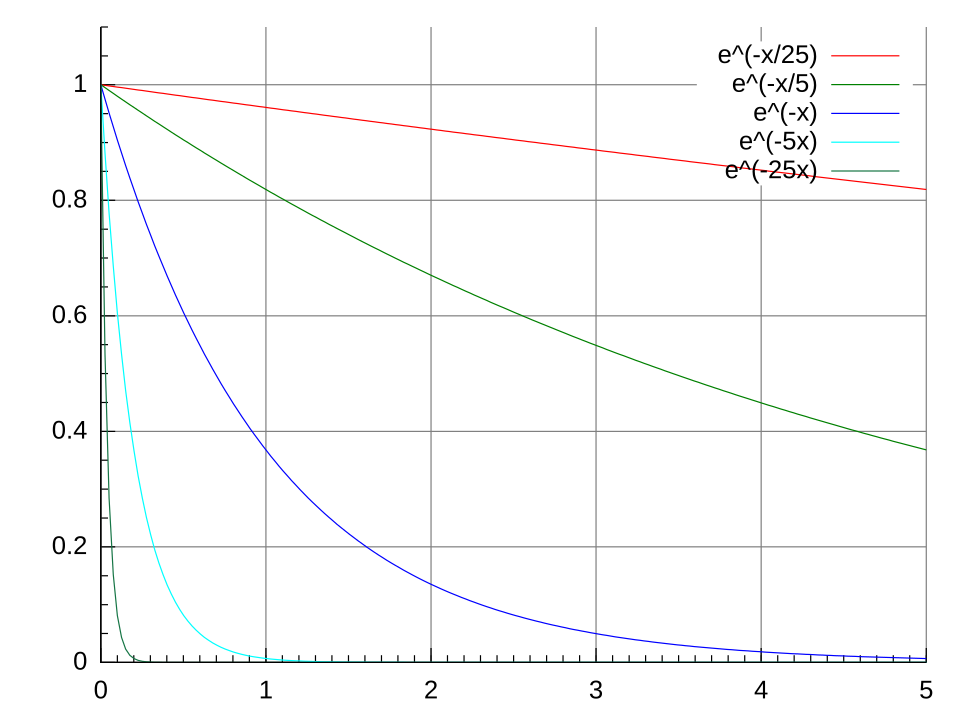
This figure shows multiple exponential decay curves, each corresponding to a different negative value of $k$ in $y = y_0 e^{kt}$. It demonstrates how the rate of decay depends on the magnitude of $k$. The comparison of several curves adds minor extra detail but remains consistent with the differential equation $\frac{dy}{dt} = ky$. Source.

Using Separation of Variables

To solve this differential equation analytically, students apply separation of variables, a method in which expressions involving $y$ are collected on one side of the equation and expressions involving $t$ appear on the other. This method is appropriate because each variable can be isolated through algebraic manipulation.

After performing any integration, it is important to recognize that solutions to this equation are always positive or always negative depending on the initial value, since the function does not cross zero unless it begins at zero. This behavior reflects exponential processes in real contexts.

Integrating Both Sides

Once variables are separated, students integrate to obtain an implicit relationship between $y$ and $t$. Recognizing the integral of the reciprocal function is crucial at this step, since the expression $\int \frac{1}{y} , dy$ involves a foundational logarithmic relationship.

After integration, the equation includes an arbitrary constant, reflecting the family of solutions. Because exponential growth and decay processes typically assume positive quantities, students often drop the absolute value when solving for $y$, depending on the context.

The next step is to rewrite the logarithmic equation in exponential form. Exponentiation removes the natural logarithm and provides a general expression representing a continuous exponential process.

Rewriting the Logarithmic Expression

Using properties of exponents, the general form simplifies into a single multiplicative constant multiplied by an exponential term. This constant absorbs the exponential of the integration constant.

This expression represents the general solution and shows that all functions satisfying $\frac{dy}{dt} = ky$ form a family of exponential curves.

This graph illustrates a typical exponential growth function, showing a curve that rises increasingly rapidly as the independent variable increases. It visually represents the qualitative behavior shared by all solutions of the form $y = y_0 e^{kt}$ when k>0. The labeling in the figure corresponds to a specific exponential function but reflects the general shape of exponential solutions. Source.

A full understanding requires interpreting how an initial condition produces a unique member of this family.

Applying the Initial Condition $y(0) = y_0$

An initial condition specifies the value of the dependent variable at a particular value of the independent variable, typically at $t = 0$. This condition enables students to determine the constant $C$ in the general solution. The value $y_0$ represents the initial amount or starting value of the modeled quantity.

After substituting $t = 0$ into the general solution and using the initial condition $y(0) = y_0$, the constant $C$ becomes equal to $y_0$. This substitution yields the familiar and widely used exponential model.

This formula appears throughout AP Calculus AB because it clearly represents how quantities evolve over time when their rates of change follow a proportional structure.

Understanding the Role of the Constant k

The constant k determines how the solution behaves over time:

• If k > 0, the function demonstrates exponential growth, increasing more rapidly as time increases.

• If k < 0, the function demonstrates exponential decay, approaching zero as time increases.

• The magnitude of k influences how quickly growth or decay occurs, with larger magnitudes producing faster changes.

These interpretations make the exponential model a powerful tool for connecting differential equations to real-world behavior.

Summary of the Solution Process

Students should follow this structured approach when solving $\frac{dy}{dt} = ky$:

• Identify the differential equation as exponential and suitable for separation of variables.

• Rearrange the equation to isolate $y$-terms on one side and $t$-terms on the other.

• Integrate both sides to obtain a logarithmic equation.

• Rewrite the result in exponential form to produce the general solution.

• Apply the initial condition $y(0) = y_0$ to obtain the particular solution $y = y_0 e^{kt}$.